Mathématiques Terminale Spécialité
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 7
Exercices
Travailler les automatismes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'oral
Envie de réaliser ces exercices à l'oral ? Enregistrez-vous !
Enregistreur audio
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Déterminer la fonction dérivée de la fonction h définie sur \mathbb{R} par h(x)=\left(x^{2}+8 x-6\right)^{4}.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Déterminer la fonction dérivée de la fonction g définie sur \mathbb{R} par g(x)=\mathrm{e}^{x^{3}+5 x-7}.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Déterminer la fonction dérivée de la fonction f définie sur \mathbb{R} par f(x)=\sqrt{x^{4}-3 x^{2}+4}.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
Que peut‑on déduire pour la fonction k à partir du tableau de signes de sa fonction dérivée k^\prime ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
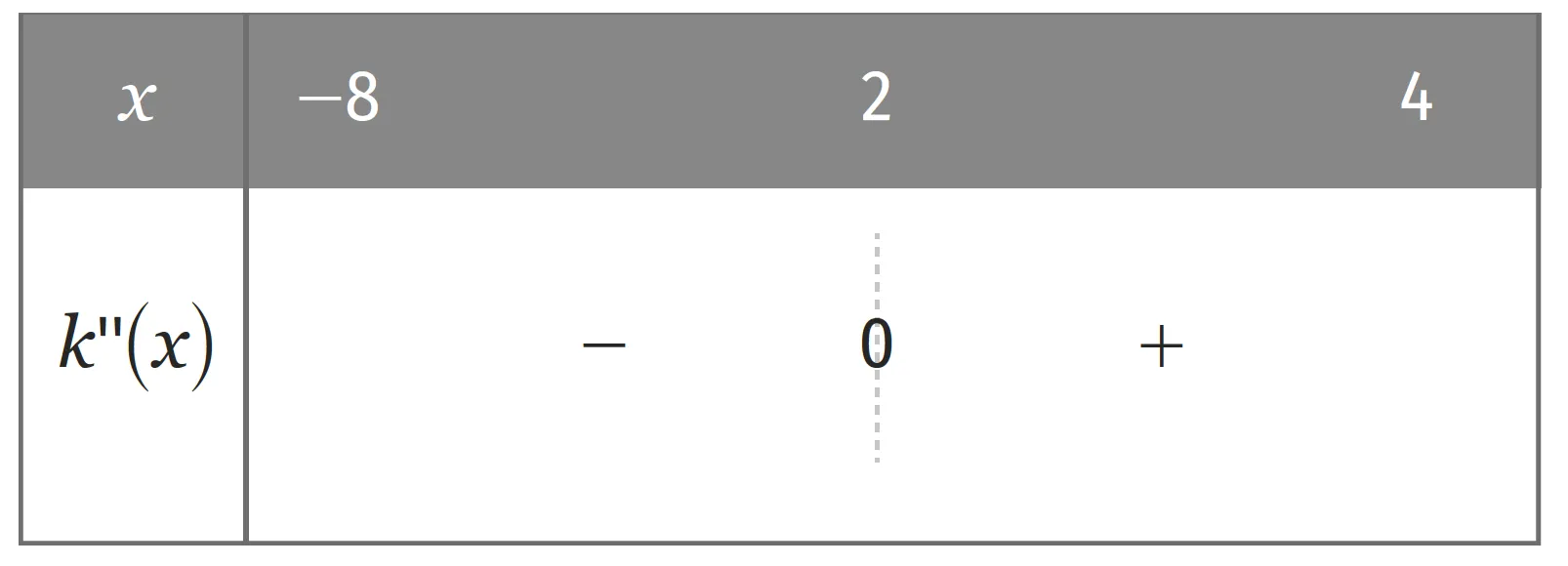
Que peut‑on déduire pour la fonction k à partir du tableau de signes de sa dérivée seconde k^{\prime\prime} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Formules de dérivation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Soit f une fonction définie sur un intervalle \text{I} par l'expression donnée.
Préciser son ensemble de dérivabilité \mathcal{D}_{f^\prime} et déterminer sa fonction dérivée f^\prime.
Préciser son ensemble de dérivabilité \mathcal{D}_{f^\prime} et déterminer sa fonction dérivée f^\prime.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
1. f(x)=\sqrt{x+\frac{1}{x}} avec \mathrm{I}=]0 ;+\infty[.
2. f(x)=\sqrt{x^{2}-3 x+5} avec \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
1. f(x)=\sqrt{x+\sqrt{x}} avec \mathrm{I}=[0 ;+\infty[.
2. f(x)=\sqrt{x^{2}+\mathrm{e}^{x}} avec \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
1. f(x)=\mathrm{e}^{x^{2}-5 x+4} avec \mathrm{I}=\mathbb{R}.
2. f(x)=\mathrm{e}^{x+\normalsize\tfrac{1}{x}} avec \mathrm{I}=\mathbb{R}^*.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
1. f(x)=\mathrm{e}^{\normalsize\tfrac{x+2}{x-7}} avec \mathrm{I}=\mathbb{R} \setminus\{7\}.
2. f(x)=\mathrm{e}^{\sqrt{x}} avec \mathrm{I}=[0 ;+\infty[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
1. f(x)=\left(x^{3}+2 x^{2}+3 x+4\right)^{5} avec \mathrm{I}=\mathbb{R}.
2. f(x)=\left(x^{3}+\frac{1}{x}+\sqrt{x}\right)^{6} avec \mathrm{I}=]0 ;+\infty[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
1. f(x)=\left(\frac{x-4}{x+3}\right)^{4} avec \mathrm{I}=\mathbb{R} \setminus\{-3\}.
2. f(x)=(\sqrt{3 x+5})^{3} avec \mathrm{I}=\left[-\frac{5}{3} ;+\infty\right[.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
1. f(x)=\left(x^{2}+3 x+2\right)^{2} \times\left(2 x^{2}-5 x+7\right)^{3} avec \mathrm{I}=\mathbb{R}.
2. f(x)=\left(x^{3}+5 x^{2}+4\right)^{2} \times \mathrm{e}^{x^{4}-8 x^{2}} avec \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
1. f(x)=\sqrt{-x^{2}+3 x-2} \times\left(x^{3}+5 x-8\right)^{3} avec \mathrm{I}=[1\,; 2].
2. f(x)=\mathrm{e}^{-x^{2}+7} \times \sqrt{x^{2}+4} avec \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
1. f(x)=\frac{\sqrt{2 x+3}}{x^{2}-x+4} avec \mathrm{I}=\left[-\frac{3}{2}\,;+\infty\right[.
2. f(x)=\frac{\mathrm{e}^{-x^{2}+5 x+4}}{x+7} avec \mathrm{I}=\mathbb{R} \setminus\{-7\}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
1. f(x)=\frac{\left(x^{3}+4\right)^{5}}{\left(x^{2}+3 x-4\right)^{3}} avec \mathrm{I}=\mathbb{R} \backslash\{-4\,; 1\}.
2. f(x)=\frac{\mathrm{e}^{2 x^{3}+x^{2}-7 x+2}}{\sqrt{x^{2}+x+1}} avec \mathrm{I}=\mathbb{R}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étude de la convexité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
Pour chacune des fonctions associées aux courbes suivantes, conjecturer la convexité et préciser approximativement les abscisses des éventuels points d'inflexion.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
La courbe ci‑dessous est celle d'une fonction f définie sur [0 ; 10] dont la tangente au point d'abscisse 5 est tracée.
Parmi les quatre courbes ci‑dessous, déterminer celle qui correspond à la courbe de la fonction dérivée f^\prime de f. Justifier la réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
Voici le tableau de variations de la fonction dérivée f^\prime d'une fonction f définie et dérivable sur [-8 ; 7].
1. En déduire le sens de variation de f.
2. Déterminer la convexité de f.
3. Tracer l'allure d'une courbe pouvant représenter f.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Voici le tableau de variations de la fonction dérivée seconde f^{\prime\prime} d'une fonction f définie et deux fois dérivable sur [-5 ; 5].
Déterminer la convexité de f et les abscisses des éventuels points d'inflexion.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
On considère la fonction f définie sur \mathbb{R} par :
f(x)=4 x^{3}-15 x^{2}-18 x+12.
On note \mathcal{C}_f la courbe représentative de f dans un repère orthogonal.
1. Dresser le tableau de variations de la fonction f.
Cliquez pour accéder à une zone de dessin
2. Établir la convexité de la fonction f.
3. Déterminer les coordonnées des éventuels points d'inflexion de \mathcal{C}_f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Voici la courbe d'une fonction f deux fois dérivable sur \mathbb{R}.
Parmi les trois courbes suivantes, déterminer celle qui représente la fonction dérivée seconde f^{\prime\prime} de f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices inversés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
1. a. Définir deux fonctions f et g non constantes sur un intervalle \mathrm{I}.
b. Déterminer l'expression de la fonction h=f \circ g.
c. Déterminer l'expression de la fonction \ell =g \circ f.
2. Déterminer les dérivées respectives des fonctions h et \ell.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
On se place dans un repère orthogonal.
1. Tracer la courbe représentative d'une fonction définie et convexe sur ]-\infty ;-2[.
Cliquez pour accéder à une zone de dessin
2. Tracer la courbe représentative d'une fonction définie sur \mathbb{R} et qui possède un point d'inflexion d'abscisse 2.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
Soit f une fonction définie et deux fois dérivable sur \mathbb{R}. Dresser un tableau de variations de f^{\prime\prime} de telle sorte que f admette deux points d'inflexion dont les abscisses soient opposées.
Cliquez pour accéder à une zone de dessin
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
