2

Avec une loi binomiale

On donne le programme ci-dessous.

from math import *
from random import *
n = int(input("Entrer la valeur du parametre n"))
N = int(input("Entrer le nombre de simulations de l'experience"))

def binom(n):
	C = 0
	# On reitere l'experience n fois
	for i in range(n):
		X = randint(1, 10)
		if X ...:
			C = C + 1
	return C

def simulation(n, N):
	simul = []
	# On simule N fois Sn
	for k in range(N):
		simul.append(binom(n))
	return simul

a = simulation(n, N)
K = 0
for i in range(0, len(a)):
	if abs(a[i] - ... ) >= sqrt(n):
		K = K + 1
print(K/N)

1. Compléter les pointillés pour simuler effectivement l’expérience avec $p = 0{,}4$.

2. Quels sont les rôles des variables $\text{C}$ et $\text{K}$ ?


3. On fixe $n = 100$. Tester le programme et noter les résultats obtenus pour $\text{N} = 50$, $\text{N} = 100$, $\text{N} = 500$ et $\text{N} = 1\:000$.


4. Comparer les résultats obtenus avec l’inégalité de Bienaymé-Tchebychev.


5. Modifier le programme pour que la valeur de $p$ puisse être choisie par l’utilisateur.

1. Ouvrir l’application GeoGebra et aller dans le menu probabilités. Choisir le mode distribution puis loi binomiale. Entrer les paramètres $n = 100$ et $p = 0{,}4$. On obtient le résultat suivant.

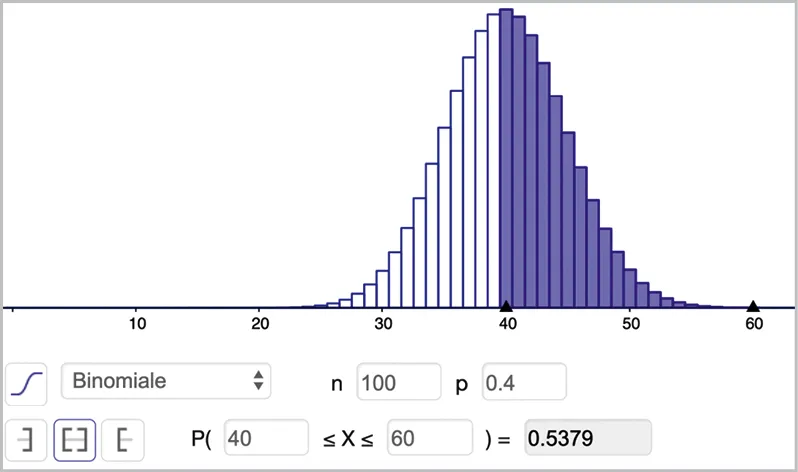
2. Traduire l’événement $\left|\mathrm{S}_{n}-n p\right| \geqslant \sqrt{n}$ dans ce cas de figure.


3. a. Quel est son événement contraire ?


b. Déterminer sa probabilité grâce au logiciel puis en déduire la probabilité voulue.


4. Comparer le résultat avec l’inégalité de Bienaymé-Tchebychev.


5. Faire le même travail pour $n = 100$ et $p = 0{,}75$.


6. L’inégalité de Bienaymé-Tchebychev semble-t-elle être une bonne majoration ? Justifier.

Pour quelle valeur de $p$ l’inégalité de Bienaymé- Tchebychev est-elle la plus large ?