Chapitre 8
Entraînement 3
Fonctions \ln(u)
Ressource affichée de l'autre côt�é.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
95
Flash
Trouver parmi les propositions suivantes celle qui correspond à l'expression de la dérivée de la fonction f définie, pour tout x \in \left]-\frac{1}{2} ;+\infty \right[, par f(x)=\ln (2 x+1). Justifier. 1. \frac{2 x}{2 x+1}
2. \frac{2}{2 x+1}
3. \frac{x^{2}+1}{2 x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
96
Flash
Sans calculer sa dérivée, dresser le tableau de variations de la fonction g définie, pour tout x \in \R, par g(x)=~\ln \left(x^{2}+4 x+5\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
97
Flash
Soit f la fonction définie, pour tout x \in \R, par f(x)=\ln \left(\frac{1}{3} x^{2}-x+1\right). Étudier les variations de f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
98
En informatique
[Communiquer.]
Étudier les variations de la fonction f définie, pour tout x \in \R, par f(x)=\ln \left(1+\mathrm{e}^{x}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
99
[Représenter.]
1. Étudier les variations de la fonction f définie, pour tout x \in \mathbb{R}, par f(x)=\ln \left(x^{2}-5 x+7\right).
2. À l'aide de la calculatrice, reproduire un tableau de valeurs de la fonction f , pour x allant de -2 à 5 avec un pas de 0,5.
3. À l'aide de ce tableau, tracer la représentation graphique de f dans un repère orthonormé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
100
[Chercher.]
On considère la fonction g définie, pour tout x \in \R, par g(x)=\ln \left(x^{4}-x^{2}+1\right). 1. Étudier les variations de g sur son ensemble de définition.
2. En déduire le nombre de solutions de l'équation g(x) = -0,2.
3. Donner une valeur approchée de chacune de ces solutions à 10^{-2} près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
101
[Communiquer.]
Étudier les variations de la fonction f définie, pour tout x>-1, par f(x)=\ln (x+1)+x^{2}+x+1.
Aide
On pourra commencer par montrer que, pour tout réel x, f^{\prime}(x)=\frac{2 x^{2}+3 x+2}{x+1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
102
[Raisonner.]
Montrer que la fonction f définie, pour tout x \in] 1 ~;~+\infty[, par \ln (x+\sqrt{x^{2}-1}) est strictement croissante sur ] 1~;~+\infty[
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
103
[Raisonner.]
Pour chacune des fonctions suivantes, déterminer la fonction dont elle est la dérivée. 1. \nobreakspace{f_{1}: x \mapsto \frac{2}{3 x}}
2. \nobreakspace{f_{2}: x \mapsto \frac{2}{3(4 x+1)}}
3. \nobreakspace{f_{3}: x \mapsto \frac{7 x-7}{x^{2}+3 x+2}}
Aide
Démontrer que \frac{x-1}{x^{2}+3 x+2}=~\frac{3}{x+2}-\frac{2}{x+1}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
104
Algo
[Raisonner.]
Soit n un entier naturel. On considère la fonction g_n définie par :
g_{n}(x)=\ln \left(x^{2 n+1}+x\right)
On note \text{I}_n l'ensemble de définition de g_n.
1.
Montrer que \left.\mathrm{I}_{n}=~\right] 0~;~+\infty[
2. Montrer que g_n est strictement croissante sur \text{I}_n.
3. a. Montrer que g_n s'annule une et une seule fois sur \text{I}_n. On note \alpha_n le réel tel que g_{n}\left(\alpha_{n}\right)=0.
b. À l'aide d'un algorithme de dichotomie, donner, pour n = 2, une valeur approchée de \alpha_2 à 10^{-2} près.
Préciser les valeurs approchées de \alpha_2 au cours de chaque étape de l'algorithme.
4. Conjecturer, à l'aide d'un logiciel de géométrie dynamique, le comportement asymptotique de \alpha_n.
2. Montrer que g_n est strictement croissante sur \text{I}_n.
3. a. Montrer que g_n s'annule une et une seule fois sur \text{I}_n. On note \alpha_n le réel tel que g_{n}\left(\alpha_{n}\right)=0.
b. À l'aide d'un algorithme de dichotomie, donner, pour n = 2, une valeur approchée de \alpha_2 à 10^{-2} près.
Préciser les valeurs approchées de \alpha_2 au cours de chaque étape de l'algorithme.
4. Conjecturer, à l'aide d'un logiciel de géométrie dynamique, le comportement asymptotique de \alpha_n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
105
[Raisonner.]
Pour chacune des questions 1., 3., 4. et 5. de cet exercice, conjecturer la réponse à l'aide de la calculatrice, puis démontrer la conjecture. On note \operatorname{argth} la fonction définie sur un intervalle \text{I} par \operatorname{argth}(x)=\frac{1}{2} \ln \left(\frac{1+x}{1-x}\right) et C sa représentation graphique.
1.
Quel est l'ensemble de définition \text{I} de la fonction \operatorname{argth} ?
2. Démontrer que la dérivée de la fonction \operatorname{argth} sur son ensemble de définition est définie par \operatorname{argth}^{\prime}(x)=~\frac{1}{1-x^{2}}.
3. Étudier les variations de la fonction \operatorname{argth} ainsi que ses limites aux bornes de son intervalle de définition.
2. Démontrer que la dérivée de la fonction \operatorname{argth} sur son ensemble de définition est définie par \operatorname{argth}^{\prime}(x)=~\frac{1}{1-x^{2}}.
3. Étudier les variations de la fonction \operatorname{argth} ainsi que ses limites aux bornes de son intervalle de définition.
4.
Déterminer une équation de la tangente à la représentation graphique de \operatorname{argth} au point d'abscisse 0. On note \text{T} cette tangente.
5. Étudier la position relative de \text{T} et C.
5. Étudier la position relative de \text{T} et C.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
106
[Calculer.]
Pour tout x \in] 1~;~+\infty[, on définit la fonction \operatorname{ch} par \operatorname{ch}(x)=\frac{e^{x}+e^{-x}}{2}. Montrer que, pour tout \nobreakspace{x \in] 1~;~+\infty[}, \operatorname{ch}(\ln (x+\sqrt{x^{2}-1}))=x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
107
[Chercher.]
On considère la fonction f définie sur \R^* par :
f(x)=\ln \left(x^{2}\right).
Parmi les trois représentations graphiques ci‑dessous, quelle est celle qui correspond à f ? Justifier.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
108
[Chercher.]
Soit n \in \mathbb{N}^{*}. On considère la fonction f_n définie par :
f_{n}(x)=\ln \left(\mathrm{e}^{n x}-x\right).
1.
Montrer que f_n est définie pour tout x \in \mathbb{R}.2. Montrer que f_n admet un minimum en x_{n}=-\frac{\ln (n)}{n}.
Préciser alors l'ordonnée du point \text{A}_n d'abscisse x_n sur la représentation graphique de f_n.
3. Conjecturer la position asymptotique de \text{A}(n) à l'aide du programme python suivant.
from numpy import log as ln
for n in range(1, 10000, 500):
print(-ln(n)/n)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
109
[Chercher.]
1. Montrer que la fonction f définie, pour tout x \in \R, par f(x)=\mathrm{e}^{x}-\mathrm{e} \times x est croissante sur [1 ~;~+\infty[. La représentation graphique de la fonction f est donnée ci‑dessous.

2. Montrer que 1 est la seule solution de l'équation f(x) = 0 sur [1 ~;~+\infty[.
3. Montrer que la suite (u_n) définie par u_0=10 et, pour tout n \in \mathbb{N}, u_{n+1}=~\ln \left(u_{n}\right)+1 est décroissante.
4. Montrer que, pour tout n \in \N, u_{n} \geqslant 1.
5. On admet que (u_n) converge et que sa limite vérifie \ln (x)-x+1=~0 Résoudre cette équation dans \R.
Aide
Démontrer que cette équation est équivalente à e \times x=e^{x} et faire le lien avec f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
110
[Chercher.]
On considère une fonction f pour laquelle il existe trois nombres réels a, b et c tels que, pour tout x~\in~\R, f(x)=\ln \left(a x^{2}+b x+c\right). La représentation graphique de f est donnée ci‑après.

Déterminer les valeurs de a, b et c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
111
[Chercher.]
On considère une fonction g pour laquelle il existe trois nombres réels a, b et c tels que, pour tout x \in \R, g(x)=\ln \left(a x^{2}+b x+c\right). La représentation graphique de g est donnée ci‑après.

Déterminer les valeurs de a, b et c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
112
[Chercher.]
On considère une fonction k pour laquelle il existe trois nombres réels a, b et c tels que, pour tout x~\in~\R, k(x)=\ln \left(a x^{2}+b x+c\right) et dont le tableau de variations est donné ci‑après.

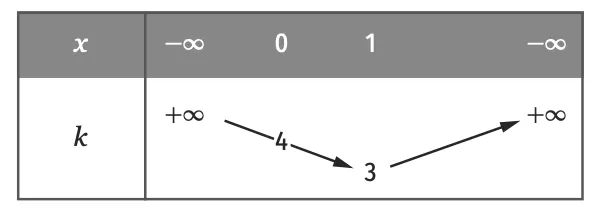
2. Que peut‑on dire du discriminant de a x^{2}+b x+c ?
3. À l'aide du tableau de variations, déterminer les valeurs de a, b et c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
113
[Chercher.]
On considère une fonction \ell pour laquelle il existe trois nombres réels a, b et c tels que, pour tout x \in]-3 ;-2[, \ell(x)=\ln \left(a x^{2}+b x+c\right) et dont le tableau de variations est donné ci‑après.
1.
Quel est le signe de a ?
2. Que peut on dire du discriminant de ax^2 + bx + c ?
3. Quelles sont les racines de ax^2 + bx + c ?
2. Que peut on dire du discriminant de ax^2 + bx + c ?
3. Quelles sont les racines de ax^2 + bx + c ?
4.
Déterminer la dérivée de \ell en fonction de a, b et c.
5. À l'aide du tableau de variations, déterminer les valeurs de a, b et c .

5. À l'aide du tableau de variations, déterminer les valeurs de a, b et c .

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
114
[Chercher.]
On considère deux fonctions f et g pour lesquelles il existe deux nombres réels a \gt 0 et b tels que, pour tout x \in \left] \frac{-b}{a} \: ; +\infty \right[, f(x)=~x^{2}+1. et g(x)=~\ln (a x+b). On suppose que la courbe de f et la courbe de g ont la même tangente au point d'abscisse 1 dans un repère orthonormé. Déterminer alors les valeurs de a et b.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
115
[Modéliser.]
On note \text{B}(x) le bénéfice réalisé par un artisan glacier pour la vente de x centaines de litres de sorbets fabriqués. On sait que, pour tout x \in[1~;~3], \mathrm{B}(x)=~-10 x^{2}+10 x+20 x \ln (x), où \text{B}(x) est exprimé en centaine d'euros.
1.
On note \text{B}^\prime, la fonction dérivée de la fonction \text{B}.
Montrer que, pour tout x \in[1~;~3], \mathrm{B}^{\prime}(x)=~-20 x+20 \ln (x)+30.
2. On donne le tableau de variations de la fonction dérivée \text{B}^\prime sur l'intervalle [1~;~3].

a. Montrer que l'équation \text{B}^\prime (x) = 0 admet une unique solution a dans l'intervalle [1~;~3]. Donner une valeur approchée de \alpha à 10^{-2}.
Montrer que, pour tout x \in[1~;~3], \mathrm{B}^{\prime}(x)=~-20 x+20 \ln (x)+30.
2. On donne le tableau de variations de la fonction dérivée \text{B}^\prime sur l'intervalle [1~;~3].

a. Montrer que l'équation \text{B}^\prime (x) = 0 admet une unique solution a dans l'intervalle [1~;~3]. Donner une valeur approchée de \alpha à 10^{-2}.
b.
En déduire le signe de \text{B}^\prime (x) sur l'intervalle [1~;~3] puis dresser le tableau de variations de la fonction \text{B} sur ce même intervalle.
3. L'artisan glacier a décidé de maintenir sa production à l'identique s'il peut atteindre un bénéfice d'au moins 850 euros. Est‑ce envisageable ?
3. L'artisan glacier a décidé de maintenir sa production à l'identique s'il peut atteindre un bénéfice d'au moins 850 euros. Est‑ce envisageable ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
116
[Chercher.]
Parmi les courbes suivantes, trouver la représentation graphique de la fonction f définie par f(x)=x \ln (x)+(1-x) \ln (1-x). Justifier.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille



