Chapitre 10
TP INFO 1
Méthode d'Euler pour une équation y^{\prime}=f
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On considère l'équation différentielle (\mathrm{E}): y^{\prime}=\mathrm{e}^{-x^{2}}. Soit f la solution de cette équation vérifiant f(0) = 1.
La méthode d'Euler est une méthode numérique qui permet de trouver une valeur approchée de la solution de
(\mathrm{E}) en utilisant les deux hypothèses vérifiées par f : f: f^{\prime}(x)=\mathrm{e}^{-x^{2}} et f(0)=1. On va utiliser cette méthode pour construire une approximation de la courbe représentative de f sur l'intervalle \mathrm{I}=[0~; 2].
On commence par choisir un pas h > 0. On pose x_0=0 et, pour tout entier naturel n, x_{n+1}=x_{n}+h puis on définit les points \mathrm{M}_{n}\left(x_{n}~; f\left(x_{n}\right)\right) qui appartiennent donc à la courbe représentative de f que l'on souhaite approcher.
Comme on ne connaît pas l'expression de la fonction f, on ne peut pas calculer directement les coordonnées de ces points.
Comme on ne connaît pas l'expression de la fonction f, on ne peut pas calculer directement les coordonnées de ces points.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions préliminaires
1. Exprimer x_1 puis x_2 en fonction de h.
2. Justifier que \frac{f\left(x_{n+1}\right)-f\left(x_{n}\right)}{h} \approx f^{\prime}\left(x_{n}\right) lorsque h est proche de 0.
3. En déduire que f\left(x_{n+1}\right) \approx f\left(x_{n}\right)+h \mathrm{e}^{-x_{n}^{2}} lorsque h est proche de 0.
4. a. Cette relation permet d'approcher les ordonnées y_n des points \mathrm{P}_n de la manière suivante : y_{n+1}=y_{n}+h \mathrm{e}^{-x_{n}^{2}}. Justifier cette égalité.
b. Justifier que y_0=1.
c. Exprimer y_1 et y_2 en fonction de h.
2. Justifier que \frac{f\left(x_{n+1}\right)-f\left(x_{n}\right)}{h} \approx f^{\prime}\left(x_{n}\right) lorsque h est proche de 0.
3. En déduire que f\left(x_{n+1}\right) \approx f\left(x_{n}\right)+h \mathrm{e}^{-x_{n}^{2}} lorsque h est proche de 0.
4. a. Cette relation permet d'approcher les ordonnées y_n des points \mathrm{P}_n de la manière suivante : y_{n+1}=y_{n}+h \mathrm{e}^{-x_{n}^{2}}. Justifier cette égalité.
b. Justifier que y_0=1.
c. Exprimer y_1 et y_2 en fonction de h.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Construire une suite de points \boldsymbol{{\mathrm{P}}_{n}(x_{n}~; y_{n})} approchant au mieux les points \boldsymbol{{\mathrm{M}}_{n}\left(x_{n}~; f\left(x_{n}\right)\right)} pour obtenir une approximation d'une primitive de la fonction \boldsymbol{x \mapsto \mathbf{e}^{-x^2}} sur \mathbf{I} à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
Dans une feuille de calcul, on construit un tableau donnant les valeurs de x_n et y_n où n est un entier naturel de 0 à 20. On entre la valeur 0 dans la cellule B2, la valeur 1 dans la cellule C2 et on choisit h = 0{,}1.
On obtient alors la feuille suivante :

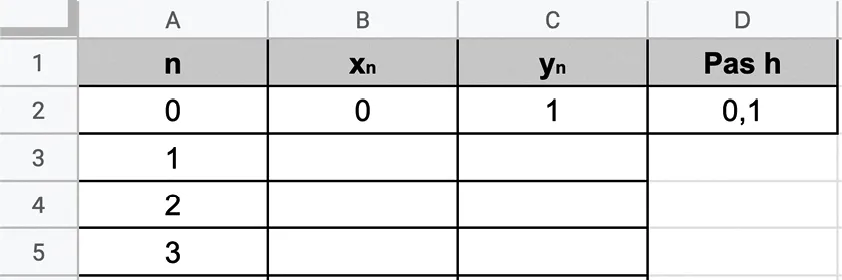
On obtient alors la feuille suivante :


1. Écrire les formules à entrer en B3 et C3 puis étirer vers le bas pour obtenir x_n et y_n.
2. Représenter la suite de points \mathrm{P}_n.
2. Représenter la suite de points \mathrm{P}_n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
On veut écrire un programme sous Python qui, pour une valeur de h saisie par l'utilisateur, calcule les coordonnées \left(x_{n}~; y_{n}\right) des points \mathrm{P}_n.
1. Déterminer la valeur de h pour obtenir 21 points équitablement répartis dans l'intervalle [0~; 2].
2. Écrire une fonction approximation d'arguments x, y et h (correspondant à x_n, y_n et h) qui retourne la valeur approchée de l'ordonnée du point \mathrm{P}_{n+1}.
a. Écrire une fonction Euler d'arguments x0, y0 et h qui retourne les abscisses x_i et les ordonnées y_i des points cherchés.
2. Écrire une fonction approximation d'arguments x, y et h (correspondant à x_n, y_n et h) qui retourne la valeur approchée de l'ordonnée du point \mathrm{P}_{n+1}.
Aide
On pensera à charger la fonction exp du module math.
a. Écrire une fonction Euler d'arguments x0, y0 et h qui retourne les abscisses x_i et les ordonnées y_i des points cherchés.
b. En utilisant par exemple le module matplotlib, représenter l'approximation graphique recherchée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
En 1901, les mathématiciens Carl Runge et Martin Wilhelm Kutta développent une méthode pour résoudre les équations différentielles du type y^{\prime}=f(t~, y) avec la condition y\left(t_{0}\right)=y_{0}.
À l'ordre 1, la méthode est similaire à la méthode d'Euler en posant y_{n+1}=y_{n}+h \times f\left(t_{n}~, y_{n}\right).
À l'ordre 2, la méthode gagne en précision en posant y_{n+1}=y_{n}+h \times f\left(t_{n}+\frac{h}{2}, y_{n}+\frac{h}{2} f\left(t_{n}~, y_{n}\right)\right).
À l'ordre 1, la méthode est similaire à la méthode d'Euler en posant y_{n+1}=y_{n}+h \times f\left(t_{n}~, y_{n}\right).
À l'ordre 2, la méthode gagne en précision en posant y_{n+1}=y_{n}+h \times f\left(t_{n}+\frac{h}{2}, y_{n}+\frac{h}{2} f\left(t_{n}~, y_{n}\right)\right).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

