Chapitre 5
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je me teste
Je sais
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Connaissant la vitesse moyenne v d'un objet, et la distance d qu'il a parcourue, je peux calculer la durée t du parcours grâce à la relation :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Rectiligne ou circulaire, uniforme ou non ?
1. La direction est obligatoirement constante.
2. La direction change au cours du mouvement.
3. Le sens est obligatoirement constant.
2. La direction change au cours du mouvement.
3. Le sens est obligatoirement constant.
4. Le sens peut changer.
5. La valeur de la vitesse est obligatoirement constante.
6. La valeur de la vitesse peut changer.
5. La valeur de la vitesse est obligatoirement constante.
6. La valeur de la vitesse peut changer.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Une définition importante.
1. Rédige la définition d'un mouvement rectiligne uniforme en utilisant les mots ou groupes de mots suivants :
Notions à utiliser : direction - sens - constant - vitesse - ne varie pas.
Notions à utiliser : direction - sens - constant - vitesse - ne varie pas.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Complète la grille de mots-croisés.
Vertical :
1. Il y en a deux pour une direction.
2. Se dit d'un mouvement dont la vitesse ne varie pas.
3. Peut être verticale ou horizontale.
4. Se dit d'un mouvement dont la direction ne varie pas.
1. Il y en a deux pour une direction.
2. Se dit d'un mouvement dont la vitesse ne varie pas.
3. Peut être verticale ou horizontale.
4. Se dit d'un mouvement dont la direction ne varie pas.
Horizontal :
5. Point de vue d'un observateur, à préciser lors de l'étude d'un mouvement.
5. Point de vue d'un observateur, à préciser lors de l'étude d'un mouvement.
Veuillez cliquer sur l'image et utiliser notre outil de dessin.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je sais faire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Assis dans un train qui démarre :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Si on lâche une balle d'une certaine hauteur :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Si je cours avec une vitesse constante de 2,5 m/s sur une distance de 75 m, la durée de ma course est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice corrigé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétence : Pratiquer le calcul numérique et le calcul littéral.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
S'arrêter avant l'obstacle.
Un deux-roues roule à la vitesse constante de 90 km/h. Un obstacle apparait devant mais il met 0,5 s avant d'actionner le frein. On donne ci-contre la chronophotographie de son mouvement par rapport au référentiel terrestre.
1. Décris le plus précisément possible le mouvement du deux-roues durant la première phase en justifiant ta réponse.
1. Décris le plus précisément possible le mouvement du deux-roues durant la première phase en justifiant ta réponse.
2. Calcule la distance en mètres parcourue par le deux-roues durant la phase 1.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étapes de la méthode
- Pour décrire un mouvement, il faut indiquer la direction, le sens. Si la direction ne change pas, alors le mouvement est rectiligne.
- Il faut aussi préciser si la vitesse varie ou non. Si la vitesse est constante, le mouvement est uniforme. Les positions de l'objet sont alors régulièrement espacées sur une chronophotographie.
- Si la distance entre les positions successives augmente ou diminue, le mouvement n'est pas uniforme.
- Il faut repérer la grandeur dont la valeur doit être calculée et celles dont les valeurs sont données, puis en déduire la formule à utiliser à l'aide du triangle de la relation. Ici, on utilisera d = v × t.
- On se rappelle que 1 km = 1 000 m et 1 h = 3 600 s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Corrigé
1. Le mouvement du deux-roues durant la phase est un mouvement rectiligne de direction horizontale, dont le sens est vers la droite et de vitesse constante car les positions successives sont régulièrement espacées. C'est donc un mouvement rectiligne uniforme.
2. Je connais la durée (0,5 s) et la vitesse (90 km/h). Pour connaitre la distance, j'utilise la formule : d = v × t, avec t en seconde et la distance d en m. Donc v doit être exprimée en m/s.
Convertissons 90 km/h en m/s :
Je peux appliquer la formule : la distance est donc 25 × 0,5 soit 12,5 m.
La distance parcourue durant la phase 1 est de 12,5 m.
2. Je connais la durée (0,5 s) et la vitesse (90 km/h). Pour connaitre la distance, j'utilise la formule : d = v × t, avec t en seconde et la distance d en m. Donc v doit être exprimée en m/s.
Convertissons 90 km/h en m/s :
- 90 km/h, signifie que l'on parcourt 90 km en 1 h ;
- soit 90 000 m en 1 h ;
- ou encore 90 000 m en 3 600 s.
Je peux appliquer la formule : la distance est donc 25 × 0,5 soit 12,5 m.
La distance parcourue durant la phase 1 est de 12,5 m.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice similaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Quelle distance pour réagir ?
Un obstacle apparait sur la trajectoire d'un motard. Le conducteur a besoin de 0,7 seconde pour actionner les freins.
1. Décris le plus précisément possible le mouvement de la moto durant la phase 2.
1. Décris le plus précisément possible le mouvement de la moto durant la phase 2.
2. Calcule la distance parcourue durant la phase 1 si le motard roule à 50 km/h.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
Au centre commercial.
Compétence
Produire et transformer des tableaux ou des documents graphiques
1. Complète le tableau suivant avec les termes « immobile » et « en mouvement ».
| Personnage | Amandine | le petit frère d'Amandine | la mère d'Amandine |
| Par rapport au sol |
|
|
|
| Par rapport à Amandine |
|
|
|
| Par rapport au petit frère d'Amandine |
|
|
|
| Par rapport à la mère d'Amandine |
|
|
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
Des records impressionnants.
Compétence
Présenter mon résultat avec l'unité adaptée
Le tableau ci-dessous présente les principaux records du monde d'athlétisme.
| Athlète ou équipe | Date | Distance | Temps |
| Usain Bolt | 2009 | 100 m | 9,58 s |
| Usain Bolt | 2009 | 200 m | 19,19 s |
| Michael Johnson | 1999 | 400 m | 43,18 s |
| Équipe de la Jamaïque | 2012 | relais 4 x 100 m | 36,84 s |
| Équipe de la Jamaïque | 2014 | relais 4 x 200 m | 1 min 18 s |
1. Classe ces records par vitesse moyenne croissante.
2. Calcule en km/h la vitesse moyenne d'Usain Bolt lors de son record sur 100 m.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
Décrire un mouvement.
Compétence
Comprendre et interpréter des tableaux ou des documents graphiques
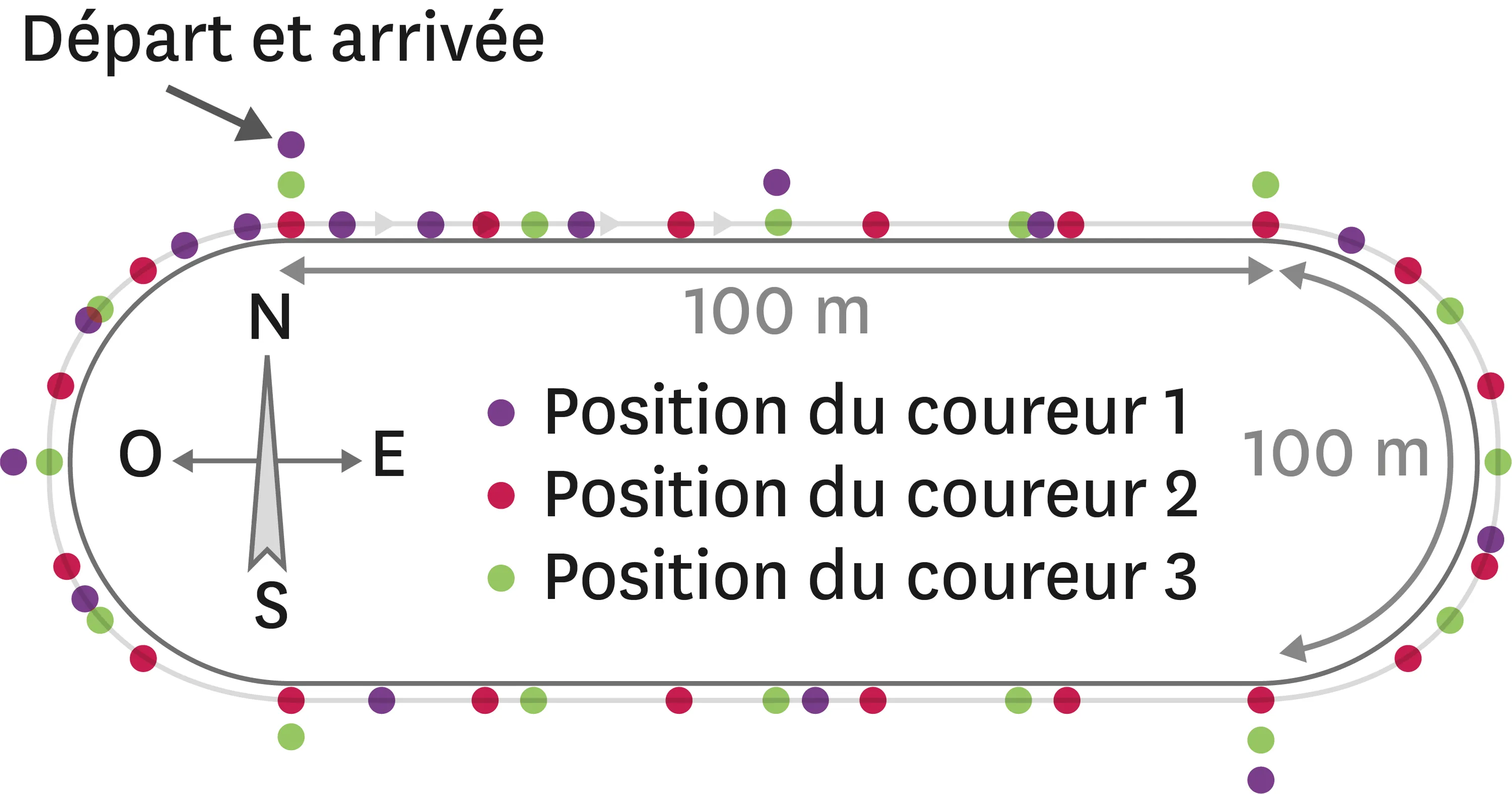
À partir des positions toutes les 10 secondes de trois élèves effectuant une course (voir l'image), complète les phrases suivantes.
1. Le mouvement de l'élève 1 de 0 à 50 s est un mouvement de direction, de sens vers et dont la valeur de la vitesse est .
2. Le mouvement de l'élève 2 de à s est un mouvement de direction Ouest-Est, de sens vers l'Est et dont la valeur de la vitesse est constante.
Le mouvement de l'élève 2 entre s et s est un mouvement dont la direction change mais la valeur de la vitesse reste la même.
1. Le mouvement de l'élève 1 de 0 à 50 s est un mouvement de direction
2. Le mouvement de l'élève 2 de
Le mouvement de l'élève 2 entre
3. Le mouvement de l'élève 3 entre s et s est un mouvement de direction Ouest-Est, de sens vers l'Ouest et dont la valeur de la vitesse ne change pas.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
La vitesse de différents véhicules.
Le tableau ci-dessous donne les vitesses maximales de différents véhicules. Mais les valeurs de la colonne de gauche ne correspondent pas à celles de droite.
1. Associe chaque vitesse maximale au véhicule correspondant.
2. Un véhicule est dit « supersonique » si sa vitesse dépasse la vitesse du son dans l'air. Quels véhicules peuvent être supersoniques ?
| Véhicule | Vitesse maximale |
| a. TGV | 1. 1 070 km/h |
| b. Fusée Ariane 5 | 2. 1 925 km/h |
| c. Avion de chasse Rafale | 3. 320 km/h |
| d. Avion de ligne Boeing 747 | 4. 17,2 km/s |
1. Associe chaque vitesse maximale au véhicule correspondant.
| Véhicule | Vitesse maximale |
| a. TGV | |
| b. Fusée Ariane 5 | |
| c. Avion de chasse Rafale | |
| d. Avion de ligne Boeing 747 |
2. Un véhicule est dit « supersonique » si sa vitesse dépasse la vitesse du son dans l'air. Quels véhicules peuvent être supersoniques ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
Un record de vitesse.
Compétence
Pratiquer le calcul numérique et le calcul littéral
1. Calcule les distances que cet escargot aurait parcourues en 20 min, puis en 1 h, s'il avait maintenu une vitesse constante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
Hyperloop.
Hyperloop est un projet de recherche sur un nouveau mode de transport, en plus des bateaux, des avions, des voitures et des trains. Il s'agit d'un tube reliant deux villes qui permettrait à des capsules de voyager à 1 102 km/h en moyenne. Le tube serait vidé d'une partie de l'air pour diminuer les frottements.
1. Calcule la durée du trajet en hyperloop entre Paris et Lyon (480 km).
2. Compare cette durée à celle du trajet effectué par un avion sur la même distance (vitesse moyenne 885 km/h).
1. Calcule la durée du trajet en hyperloop entre Paris et Lyon (480 km).
2. Compare cette durée à celle du trajet effectué par un avion sur la même distance (vitesse moyenne 885 km/h).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une notion, trois exercices
Différenciation
Compétence : Présenter mon résultat avec l'unité adaptée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16-AVous rouliez encore trop vite…
1. Donne la distance du trajet Paris-Rouen.
2. Rappelle la formule qui permet de calculer la durée d'un trajet en connaissant la distance du trajet et la vitesse v.
3. Calcule alors la durée en heures du trajet, connaissant la distance Paris-Rouen, pour une voiture roulant à 130 km/h.
4. Calcule la durée en heures du trajet Paris-Rouen pour un automobiliste roulant à 140 km/h.
5. Calcule l'écart entre les deux durées précédentes en heures.
6. Convertis cet écart en minutes.
2. Rappelle la formule qui permet de calculer la durée d'un trajet en connaissant la distance du trajet et la vitesse v.
3. Calcule alors la durée en heures du trajet, connaissant la distance Paris-Rouen, pour une voiture roulant à 130 km/h.
4. Calcule la durée en heures du trajet Paris-Rouen pour un automobiliste roulant à 140 km/h.
5. Calcule l'écart entre les deux durées précédentes en heures.
6. Convertis cet écart en minutes.
7. Recommence ces six étapes pour le trajet Paris-Nancy.
8. Explique en quelques phrases pourquoi l'image ci-contre permet de sensibiliser les automobilistes quant à leur décision de rouler plus vite.

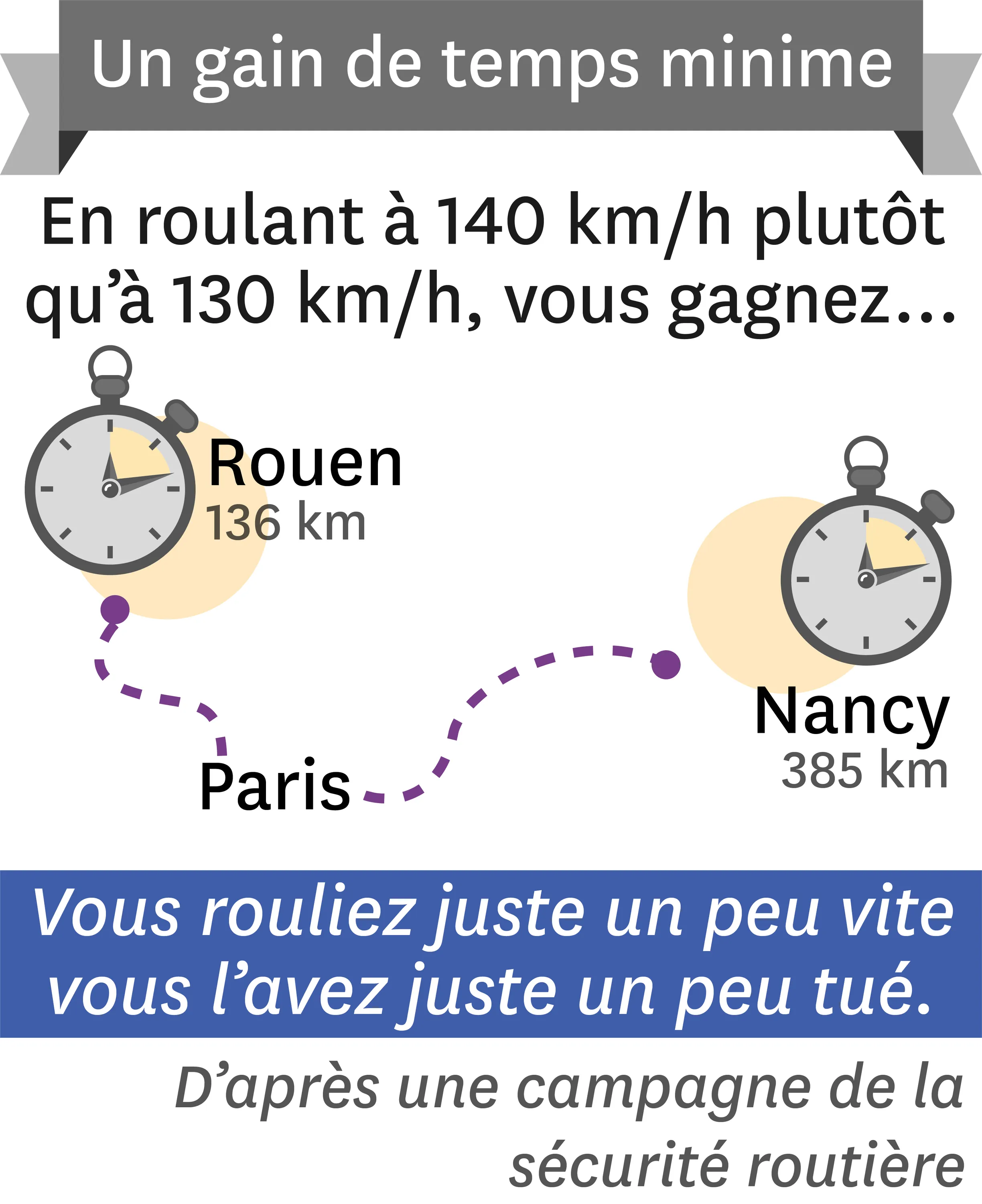
8. Explique en quelques phrases pourquoi l'image ci-contre permet de sensibiliser les automobilistes quant à leur décision de rouler plus vite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16-BVous rouliez toujours trop vite…
1. Calcule la durée en heures des trajets Paris-Le Mans et Paris-Besançon pour un automobiliste roulant à 130 km/h.
2. Calcule la durée en heures, minutes et secondes des trajets Paris-Le Mans et Paris-Besançon pour un automobiliste roulant à 140 km/h.
3. Calcule la différence de durée entre ces deux trajets en minutes.
4. Explique en quelques phrases pourquoi l'image permet de sensibiliser les automobilistes quant aux conséquences éventuelles de leur décision de rouler plus vite.

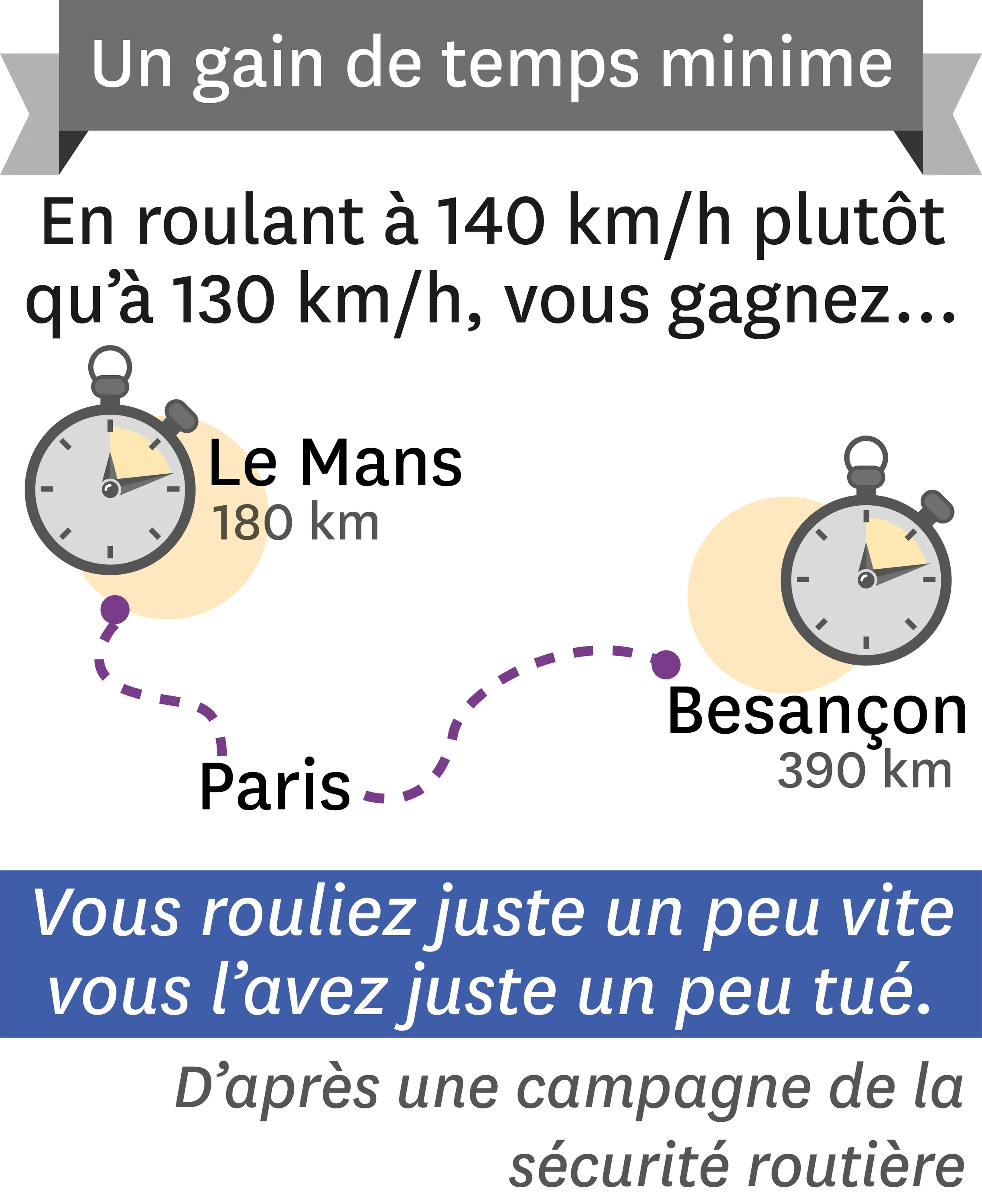
2. Calcule la durée en heures, minutes et secondes des trajets Paris-Le Mans et Paris-Besançon pour un automobiliste roulant à 140 km/h.
3. Calcule la différence de durée entre ces deux trajets en minutes.
4. Explique en quelques phrases pourquoi l'image permet de sensibiliser les automobilistes quant aux conséquences éventuelles de leur décision de rouler plus vite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16-CVous rouliez juste un peu vite…
Dans le but de sensibiliser les conducteurs au respect de la vitesse, une campagne d'affichage est mise en place.
1. Complète la première affiche en indiquant le nombre de minutes gagnées en roulant à 140 km/h au lieu de 130 km/h pour les deux trajets présentés.
2. Explique pourquoi l'image permet de sensibiliser les automobilistes vis-à-vis des excès de vitesse.

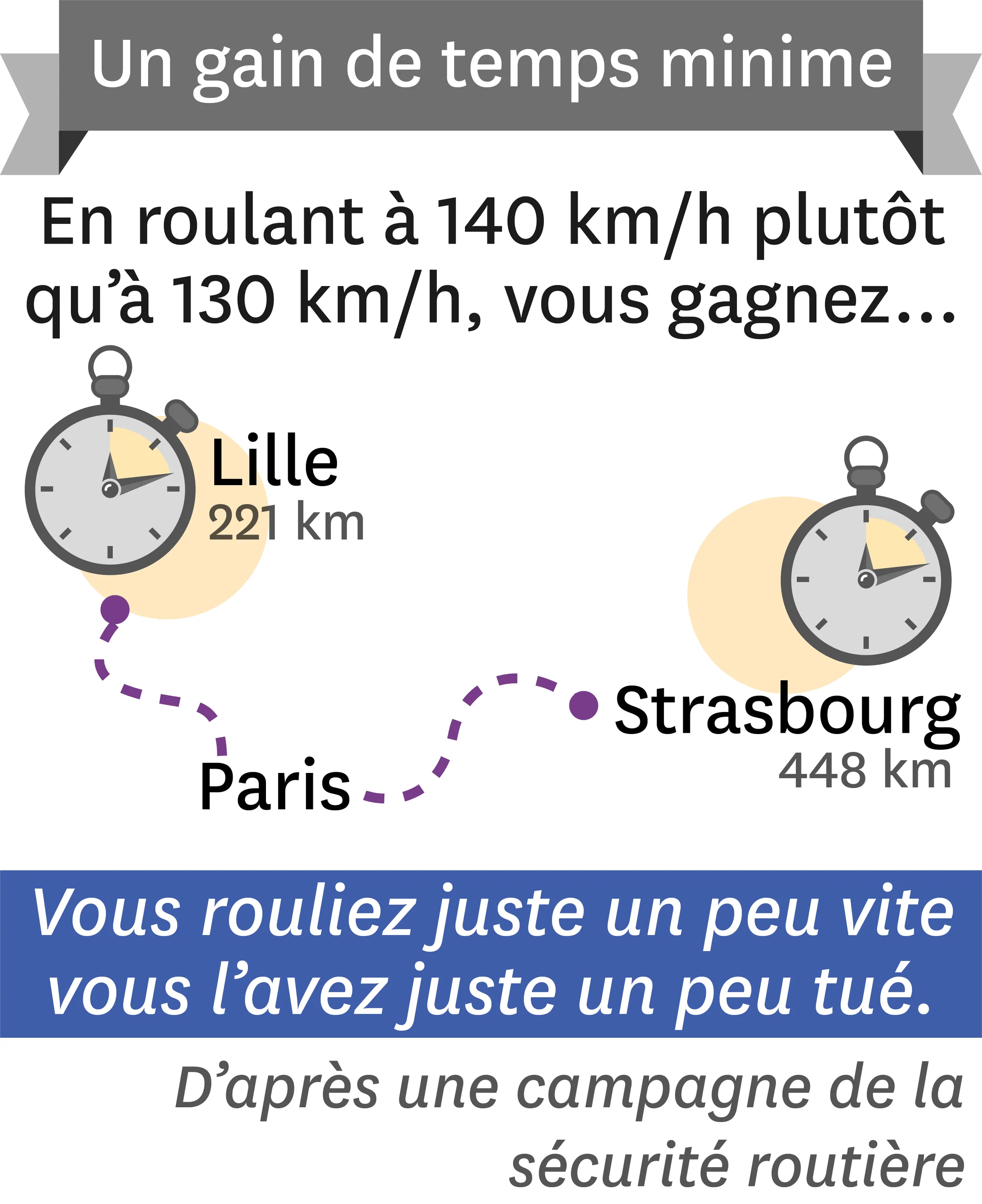
1. Complète la première affiche en indiquant le nombre de minutes gagnées en roulant à 140 km/h au lieu de 130 km/h pour les deux trajets présentés.
2. Explique pourquoi l'image permet de sensibiliser les automobilistes vis-à-vis des excès de vitesse.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Un challenge réussi.
Le 14 octobre 2012, l'Autrichien Felix Baumgartner atteint l'altitude de 39 376 m à l'aide d'un ballon d'hélium. À cette altitude, il se jette dans le vide et tombe vers le sol durant une chute libre de 4 min 19 s, parcourant ainsi 36 529 m. Durant cette phase, il atteint la vitesse de pointe de 1 357,6 km/h. Au bout d'un certain temps, il ouvre son parachute pour atterrir sain et sauf après une chute d'une durée totale de 9 min 3 s.
1. Rajoute sur l'image les légendes suivantes : « départ du saut », « mouvement rectiligne uniforme », « mouvement rectiligne dont la valeur de la vitesse augmente », « ouverture du parachute ».
2. Calcule la valeur de la vitesse moyenne de Felix Baumgartner en m/s durant la phase de chute libre.
3. Convertis la valeur de la vitesse de pointe en m/s. Explique la différence entre cette valeur et la valeur de vitesse moyenne calculée à la question 2.
1. Rajoute sur l'image les légendes suivantes : « départ du saut », « mouvement rectiligne uniforme », « mouvement rectiligne dont la valeur de la vitesse augmente », « ouverture du parachute ».
2. Calcule la valeur de la vitesse moyenne de Felix Baumgartner en m/s durant la phase de chute libre.
3. Convertis la valeur de la vitesse de pointe en m/s. Explique la différence entre cette valeur et la valeur de vitesse moyenne calculée à la question 2.
4. Calcule la valeur de la vitesse moyenne de Felix Baumgartner en m/s durant la phase où son parachute est ouvert.
5. Felix Baumgartner a-t-il dépassé la vitesse du son dans l'air ? Justifie ta réponse.


5. Felix Baumgartner a-t-il dépassé la vitesse du son dans l'air ? Justifie ta réponse.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Un lancer en pleine lumière.
L'image représente un lancer de ballon. Le soleil étant au zénith, l'ombre du ballon se projette sur le sol.

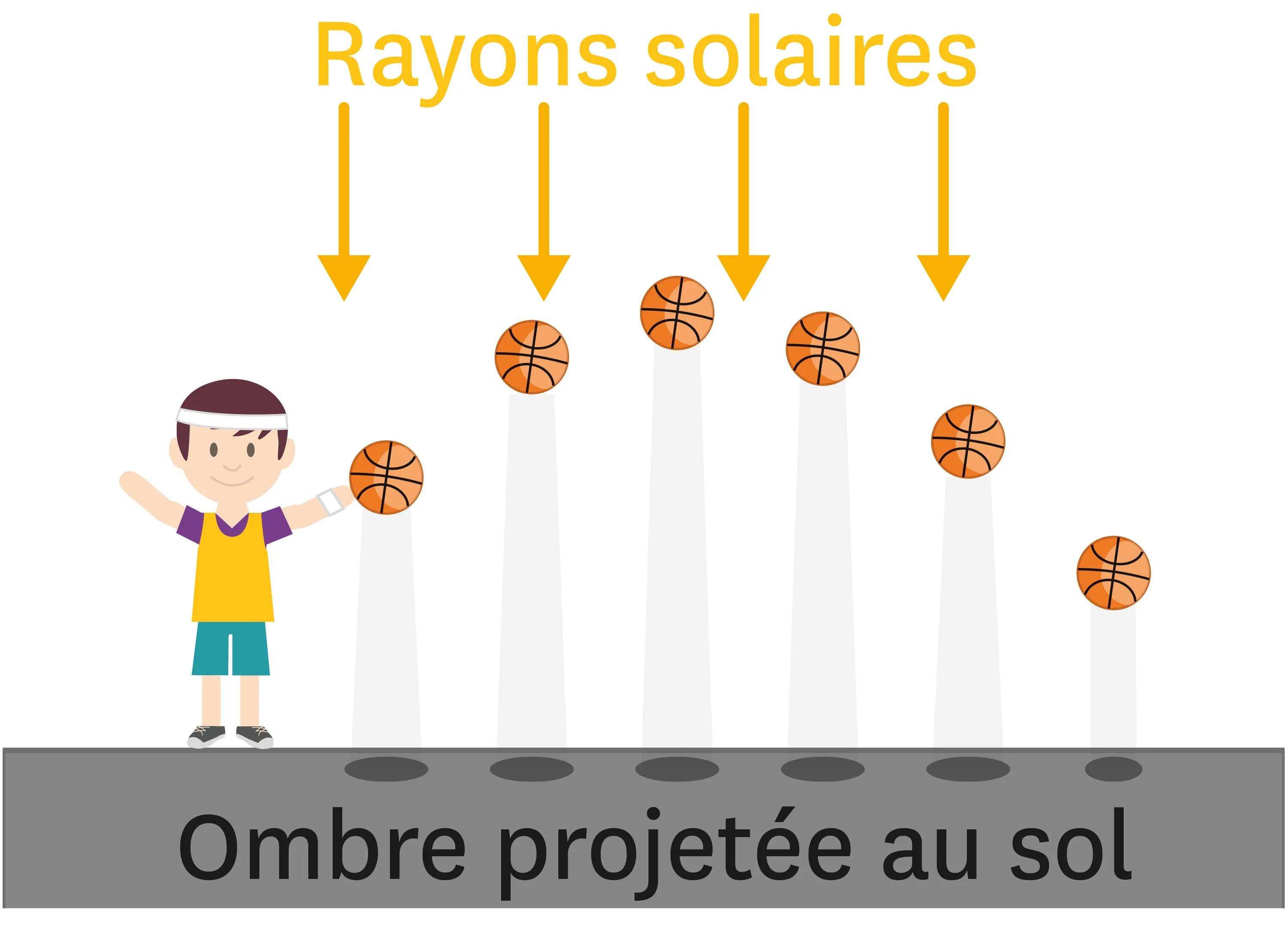
1. La direction du mouvement du ballon change-t-elle au cours du temps ?
2. Comment évolue la valeur de la vitesse du ballon au cours de ce lancer ?
3. Décris le mouvement de l'ombre du ballon durant le lancer.


1. La direction du mouvement du ballon change-t-elle au cours du temps ?
2. Comment évolue la valeur de la vitesse du ballon au cours de ce lancer ?
3. Décris le mouvement de l'ombre du ballon durant le lancer.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Une vitesse astronomique.
Le 14 juillet 2015, la sonde New Horizons survole la planète naine Pluton. L'infographie ci-dessous présente plusieurs informations relatives à ce survol.
1 Précise la direction et le sens du mouvement rectiligne de la sonde.
2 Le mouvement est-il uniforme ? Justifie ta réponse.
3 Pour quelles raisons peut-on dire que la vitesse moyenne de la sonde lors de ce survol est d'environ 13,8 km/s ? Observe bien les données numériques de l'infographie.
4 À l'aide de cette vitesse moyenne, calcule la distance parcourue en km par la sonde entre 11 h et 15 h ce 14 juillet 2015.

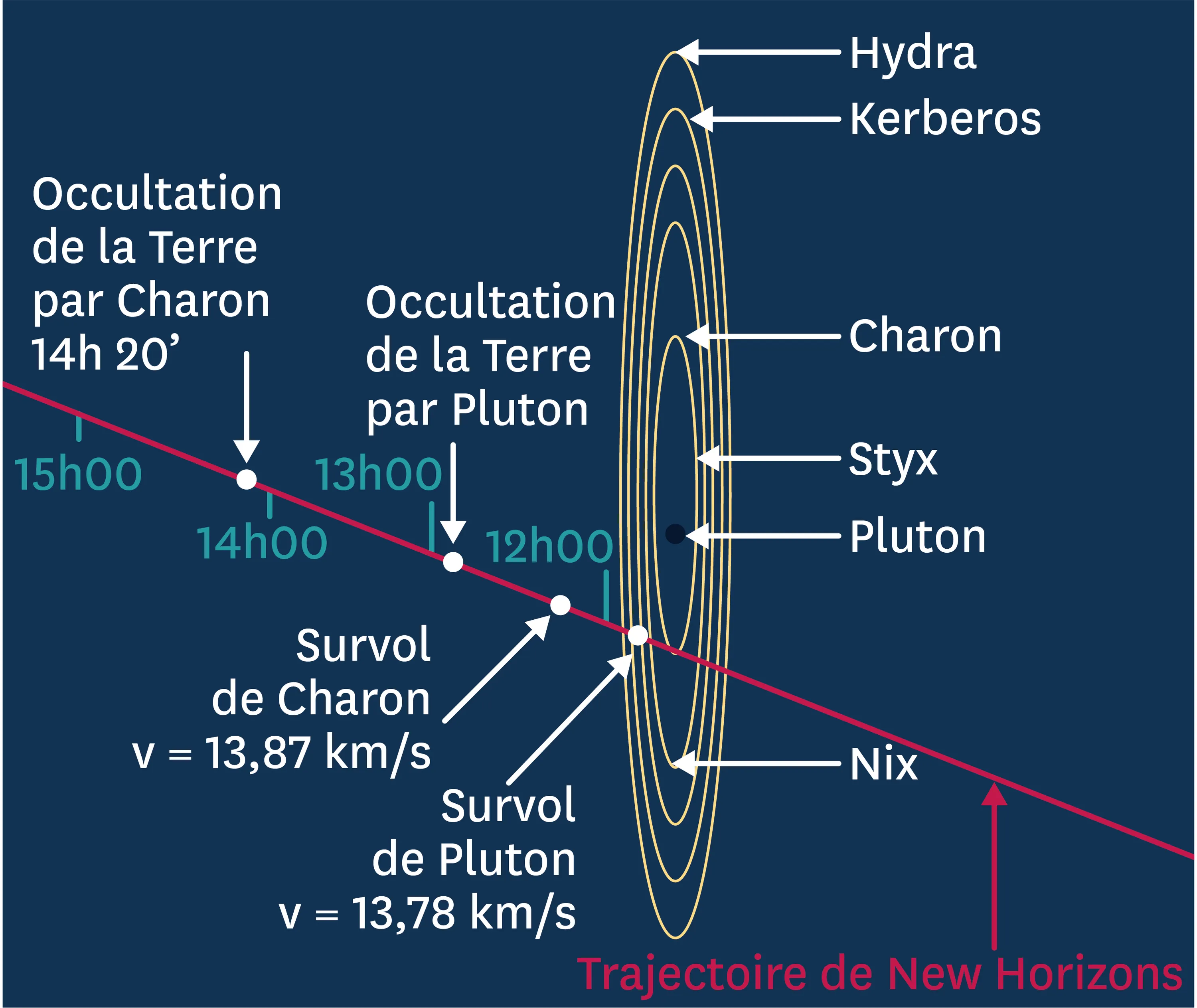
1 Précise la direction et le sens du mouvement rectiligne de la sonde.
2 Le mouvement est-il uniforme ? Justifie ta réponse.
3 Pour quelles raisons peut-on dire que la vitesse moyenne de la sonde lors de ce survol est d'environ 13,8 km/s ? Observe bien les données numériques de l'infographie.
4 À l'aide de cette vitesse moyenne, calcule la distance parcourue en km par la sonde entre 11 h et 15 h ce 14 juillet 2015.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Un satellite géostationnaire.
Le satellite Météosat est situé à 36 000 km du sol terrestre au-dessus de l'Europe. Il parcourt son orbite circulaire à vitesse constante en 24 h par rapport au centre de la Terre.
1. Sachant que le rayon de la Terre est de 6 400 km, quelle est la distance parcourue par le satellite en 24 h ?
2. Calcule la vitesse en km/h du satellite par rapport au centre de la Terre.
2. Calcule la vitesse en km/h du satellite par rapport au centre de la Terre.
3. Quel est le mouvement de ce satellite par rapport au sol européen ? Justifie ta réponse.
4. À partir de la réponse précédente, explique pourquoi Météosat est un satellite géostationnaire.
4. À partir de la réponse précédente, explique pourquoi Météosat est un satellite géostationnaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21Des trajectoires bien compliquées.

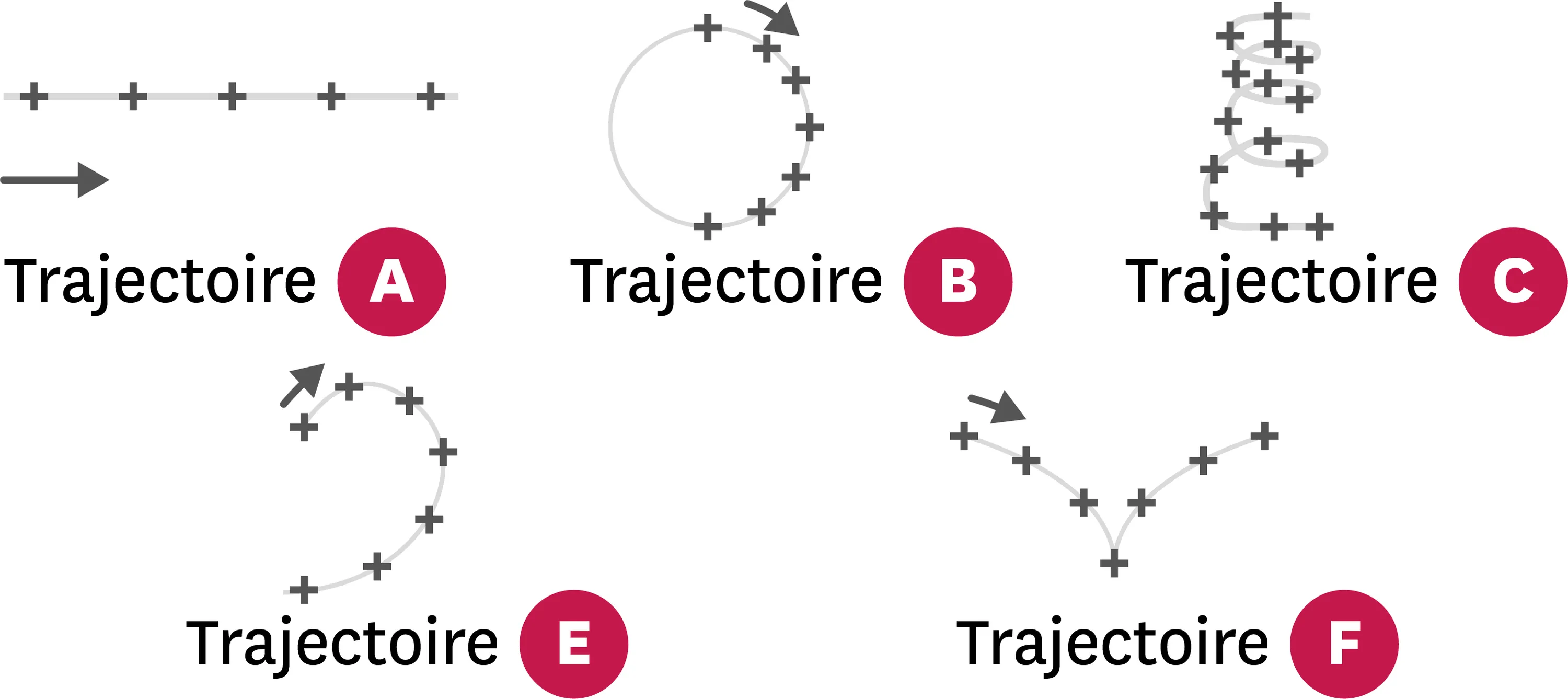
Les images suivantes présentent des trajectoires de différents points. Associe les trajectoires aux différents mouvements décrits :
| A | B | C | E | F |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
La collision aura-t-elle lieu ?
Compétence
Pratiquer le calcul numérique et le calcul littéral
Naomi roule à 50 km/h en voiture. Son temps de réaction est d'une seconde. Tout à coup, un chien surgit à 22 m devant elle.
1. Convertis la vitesse de la voiture en m/s.
2. La valeur de la vitesse change-t-elle avant que Naomi réagisse et actionne le frein ?
3. Calcule alors la distance parcourue durant le temps de réaction. La distance de freinage de sa voiture est de 3,5 m pour une vitesse de 25 km/h. Mais on sait que la distance de freinage d'un véhicule est multipliée par quatre si la vitesse est doublée.
4. Calcule la distance que mettra sa voiture pour freiner, distance appelée distance de freinage.
5. Va-t-elle percuter le chien ? Justifie ta réponse.

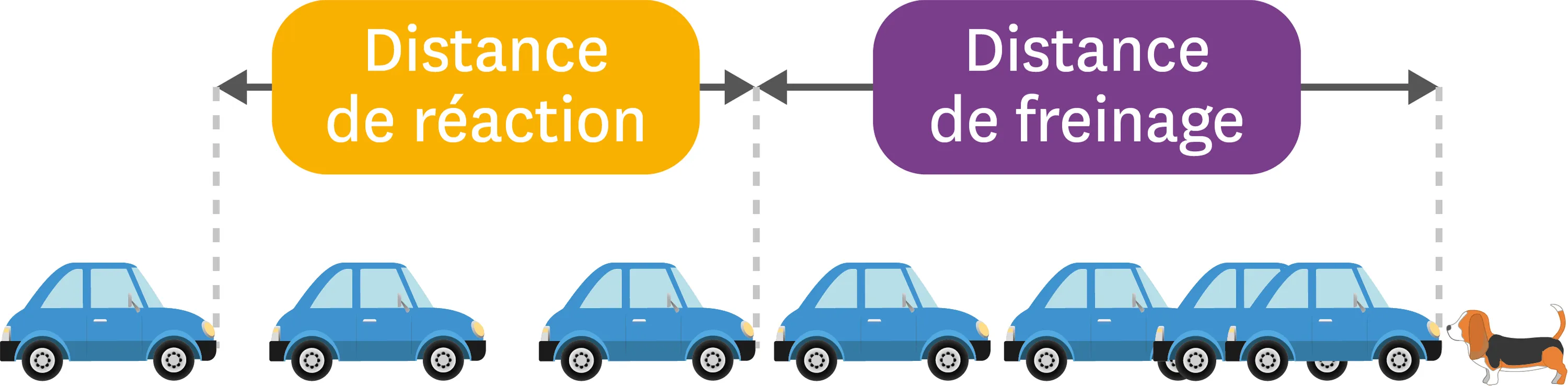
5. Va-t-elle percuter le chien ? Justifie ta réponse.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Parachute ascensionnel.
Compétence
Interpréter des résultats
Durant leurs vacances, Alissa expérimente le parachutisme ascensionnel. Première phase : au départ, elle est sur la plage. Puis le bateau démarre. Deuxième phase : au bout d'un certain temps la corde se tend et, Alissa voit son parachute se gonfler et elle quitte le sol. Troisième phase : Alissa reste à une altitude constante alors que le bateau continue son trajet en ligne droite à vitesse constante.
1. Durant la première phase, explique pourquoi le mouvement du bateau n'est pas uniforme par rapport à Alissa.
2. Durant la seconde phase, pour quel référentiel le mouvement d'Alissa est un mouvement circulaire ?
3. Durant la troisième phase, quel est le mouvement du bateau par rapport à Alissa ?
4. Durant la troisième phase, décris le mouvement du bateau par rapport au sol.
5. Durant quelle(s) phase(s) Alissa est-elle immobile par rapport au sac contenant son parachute ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Un hamster en liberté.
Compétence
Interpréter des résultats
Pour se défouler, les hamsters dans leur cage font régulièrement du sport en courant dans une roue. On peut aussi les sortir de leur cage et les mettre dans une balle translucide, pour qu'ils puissent explorer la maison en toute sécurité.
1. Quand il utilise la roue de sa cage, quel est le mouvement du hamster par rapport au sol ?
2. Quelle est la trajectoire d'un point situé sur le bord de la roue quand le hamster l'utilise dans sa cage ?
3. Quand il est dans sa balle translucide et court à vitesse constante, quel est le mouvement du hamster par rapport au sol ?
4. Dans ce cas, comment filmer ce hamster pour qu'il reste au centre de l'image ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je résous un problème
Compétence : Mettre en œuvre un raisonnement logique simple pour résoudre un problème.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La collision d'un choc d'une voiture roulant à une certaine vitesse contre un obstacle fixe est comparée au choc d'une personne tombant d'un immeuble.
À partir des documents suivants, complète les phrases suivantes :
À partir des documents suivants, complète les phrases suivantes :
- Une collision à 50 km/h revient à sauter du étage d'un immeuble.
- Une collision à 90 km/h revient à sauter du étage d'un immeuble.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Tableau donnant la hauteur h d'une chute libre en fonction de la durée t de la chute et de la vitesse v atteinte à cette hauteur.
| h en m | 4,5 | 9 | 10 | 19 | 31 |
| t en s | 0,95 | 1,34 | 1,4 | 1,94 | 2,5 |
| v en m/s | 9,5 | 13,4 | 14 | 19,4 | 25 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Indice.
La hauteur moyenne d'un étage est de 3 m.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices supplémentaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Au centre commercial.
Dans un centre commercial, deux rampes d'escalators parallèles fonctionnent en sens opposé. L'escalator A fait monter les clients au niveau supérieur, alors que l'escalator B les fait descendre. Amandine reste sur l'une des marches de l'escalator A, alors que son petit frère s'amuse à descendre les marches de cet escalator, tout en étant immobile par rapport au sol. Au même moment, elle aperçoit sa mère qui les attend au niveau supérieur. Sur l'escalator B, Bruno vit la même situation : Bruno reste sur l'une des marches, tandis que sa petite sœur s'amuse à les monter, tout en restant immobile par rapport au sol.
1. Remplis le tableau suivant avec les termes “immobile” et “en mouvement”.
2. Si l'escalator B faisait monter les clients à la même vitesse que l'escalator A, que devrait faire la petite sœur de Bruno pour être immobile par rapport au petit frère d'Amandine ?
1. Remplis le tableau suivant avec les termes “immobile” et “en mouvement”.
| Personnage | Amandine | Le petit frère d'Amandine | Bruno | La petite sœur de Bruno | La mère d'Amandine |
| Par rapport au sol |
|
|
|
|
|
| Par rapport à Amandine |
|
|
|
| |
| Par rapport au petit frère d'Amandine |
|
|
|
| |
| Par rapport à Bruno |
|
|
|
| |
| Par rapport à la sœur de Bruno |
|
|
|
| |
| Par rapport à la mère d'Amandine |
|
|
|
|
2. Si l'escalator B faisait monter les clients à la même vitesse que l'escalator A, que devrait faire la petite sœur de Bruno pour être immobile par rapport au petit frère d'Amandine ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Cela valait le déplacement ...
À la fin d'octobre 2014, l'ATV Georges Lemaître, accroché à la station spatiale internationale, est utilisé pour éloigner la station d'une zone possible de collision avec un débris du satellite russe Cosmos 2251 : à la vitesse de 1,8 km/h, il déplace les 420 tonnes de la station d'une distance de 1 000 m.
1. Calcule la durée du déplacement par l'ATV Georges Lemaître en minutes.
1. Calcule la durée du déplacement par l'ATV Georges Lemaître en minutes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Réfléchir à une méthode.
1. Associe les méthodes de calcul à mettre en œuvre aux différentes questions.
| Multiplier la valeur de la vitesse par 3 600 pour connaître la distance parcourue en une heure. | |
| Rechercher la distance parcourue dans l'énoncé et la durée du parcours, puis diviser la distance par cette durée. | |
| Convertir les vitesses dans une même unité. | |
| Multiplier la vitesse par 3 600 pour savoir la distance parcourue en 1 h, puis diviser par 1 000 pour la convertir. | |
| Diviser cette vitesse par 3 600 pour connaître la distance parcourue en 1 s, puis multiplier par 1 000 pour la convertir en m. |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Un entrainement.
Lors d'un entrainement, un élève effectue une course sur une piste en ligne droite. La distance qu'il parcourt est mesurée par une application à l'aide de son smartphone pour différentes durées. Les résultats sont collectés dans le tableau ci-dessous
1. Construis le graphique de la distance en fonction du temps pour ce coureur.
2. Combien de temps dure la phase de mouvement rectiligne uniforme ?
3. Calcule la vitesse en m/s de ce coureur durant cette phase. S'agit-il de sa vitesse maximale ou de sa vitesse de pointe ?
4. Compare cette valeur à sa vitesse moyenne.
5. Convertis la valeur de sa vitesse de pointe en km/h.
| Distance parcourue (en m) | 0 | 0,33 | 1,33 | 3 | 6 | 9 | 12 | 15 | 18 | 20,25 | 21 | 21 |
| Temps (en s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1. Construis le graphique de la distance en fonction du temps pour ce coureur.
2. Combien de temps dure la phase de mouvement rectiligne uniforme ?
3. Calcule la vitesse en m/s de ce coureur durant cette phase. S'agit-il de sa vitesse maximale ou de sa vitesse de pointe ?
4. Compare cette valeur à sa vitesse moyenne.
5. Convertis la valeur de sa vitesse de pointe en km/h.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29La course.
Trois élèves font une course sur une ligne droite. Thibault démarre lentement puis dépasse Yazid. Mais tous les deux n'arrivent pas à rattraper Gina avec laquelle l'écart n'a fait qu'augmenter tout au long de la course. Dans quel référentiel, Thibault peut-il dire...
1. qu'il est immobile ?
2. qu'il avance ?
3. qu'il recule ?
1. qu'il est immobile ?
2. qu'il avance ?
3. qu'il recule ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parcours de compétences
Compétence : Comprendre et interpréter des tableaux ou des documents graphiques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
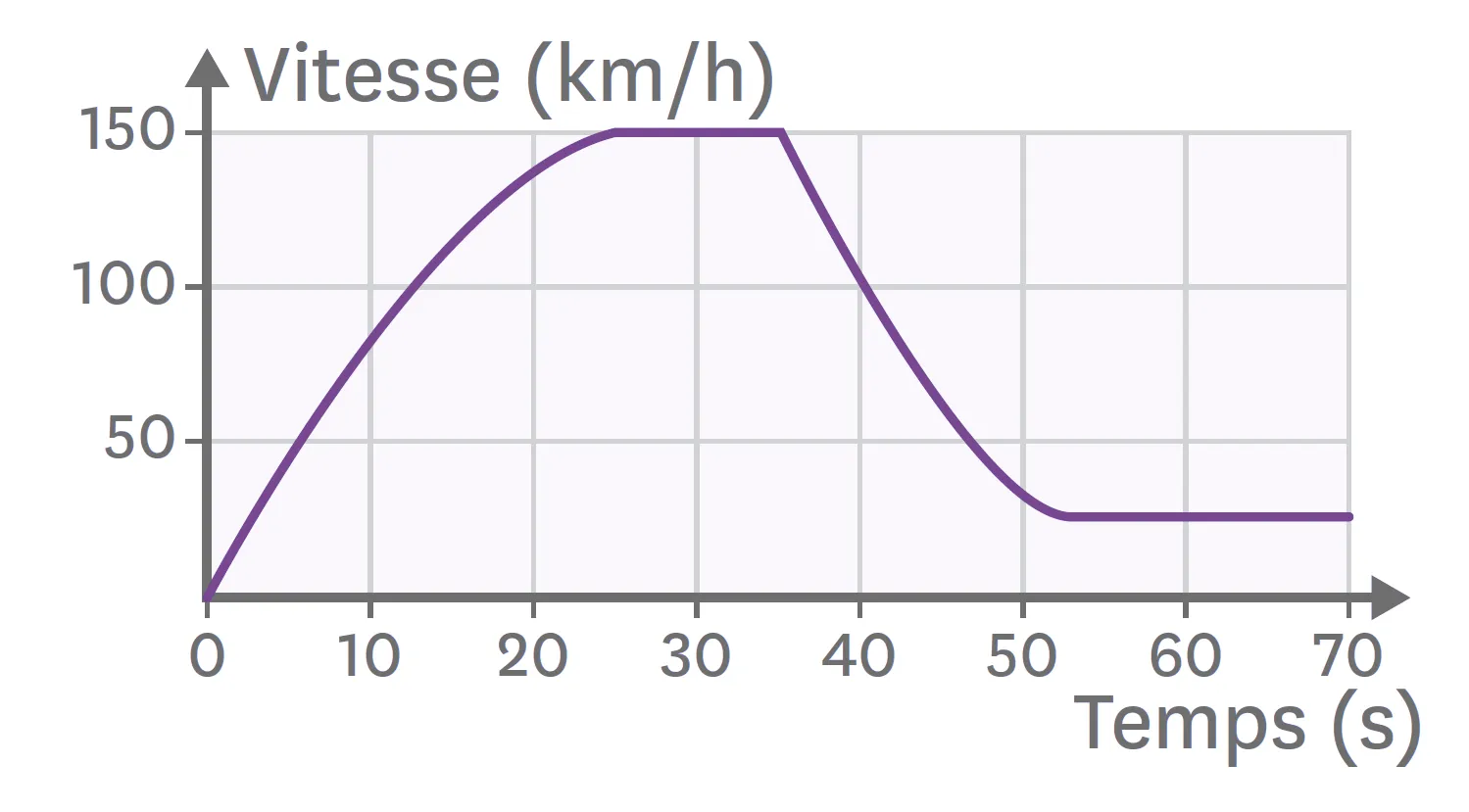
Le graphe ci-contre représente l'évolution de la vitesse d'un parachutiste au cours du temps lors du saut, depuis l'avion.
1. À l'aide du graphique, que peux-tu dire sur la première partie du saut ? À quel instant le parachutiste ouvre-t-il son parachute ? Justifie ta réponse.
1. À l'aide du graphique, que peux-tu dire sur la première partie du saut ? À quel instant le parachutiste ouvre-t-il son parachute ? Justifie ta réponse.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 1
Je repère les éléments en lien avec le thème étudié dans un tableau, un graphique, un diagramme ou un schéma.
Coup de pouce
Quelles sont les grandeurs et les unités de l'axe des abscisses et des ordonnées ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 2
J'extrais une donnée d'un tableau, d'un graphique, d'un diagramme ou d'un schéma.
Coup de pouce
Quelle est la valeur de la vitesse à t = 10 s ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 3
Je relie entre elles les informations extraites d'un tableau, d'un graphique ou d'un schéma.
Coup de pouce
Comment évolue la vitesse entre 0 s et 25 s ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 4
J'interprète des tableaux, des graphiques, des diagrammes ou des schémas, en structurant mes arguments.
Coup de pouce
Lorsque le sauteur ouvre son parachute, explique comment sa vitesse évolue.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

