Mathématiques Cycle 4
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et g éométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 1
Les maths autrement
Le crible d'Ératosthène
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Présentation
Ératosthène
Ératosthène (276-194 av. J.-C.) est un astronome, géographe, philosophe et mathématicien grec de l'Antiquité. En mathématiques, il établit le crible d'Ératosthène qui permet de déterminer tous les nombres premiers inférieurs à un nombre entier fixé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- J'utilise des cas particuliers pour orienter ma démarche de résolution.
- Je comprends la modélisation numérique ou géométrique d'une situation.
- J'écris et j'exécute un programme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étape 1Le crible
Dans un tableau de 10 cases par 10, retrouvez lʼensemble des nombres de 1 à 100.
1. Barrez les nombres non premiers.
- Barrez le 1.
- 2 est premier, entourez-le puis barrez tous les multiples de 2.
- Le premier nombre non barré après 2 est 3, c'est un nombre premier. Entourez-le et rayez tous les multiples de 3, sauf 3.
2. Pourquoi, à chaque étape, le premier nombre non barré est-il premier ?
3. Que pouvez-vous dire du premier multiple à barrer par rapport au dernier nombre premier entouré ?
4. Pourquoi peut-on sʼarrêter après avoir barré les multiples de 7 autres que 7 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étape 2Un programme à créer en groupe
En groupe, utilisez les blocs suivants (qui sont dans le désordre) pour créer un programme qui demande à lʼutilisateur de donner un nombre et teste si ce nombre est premier.
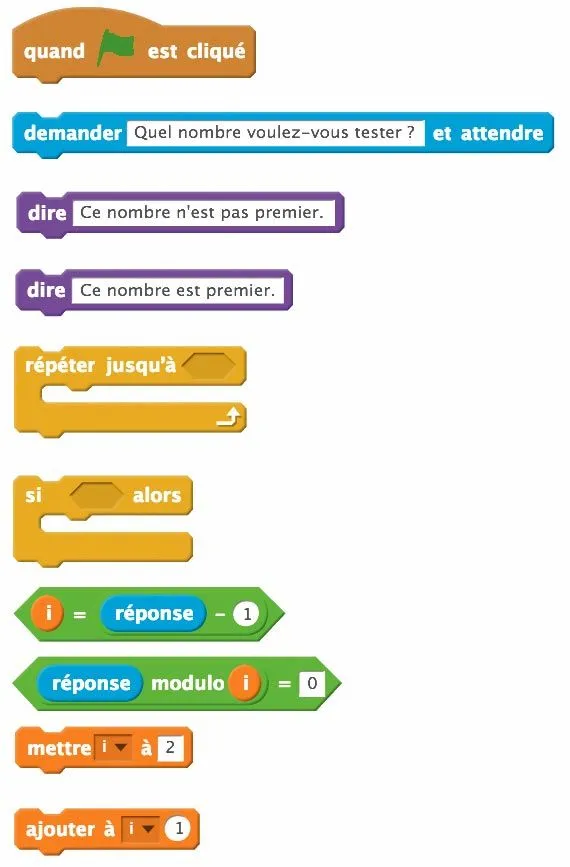
On appelle n le nombre entré par lʼutilisateur. Il faut créer une variable, qui ira de 2 à n-1 et tester si cette variable est un diviseur de n.
Si lʼune des valeurs données à la variable divise n, le lutin dit que le nombre nʼest pas premier et lʼalgorithme est stoppé. Sinon, après lʼensemble des tests, il indique que le nombre est premier.
Si lʼune des valeurs données à la variable divise n, le lutin dit que le nombre nʼest pas premier et lʼalgorithme est stoppé. Sinon, après lʼensemble des tests, il indique que le nombre est premier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Envie d'en savoir plus ? Découvrez :
- une ;
- une par Ératosthène.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
