Sommaire
Mes pages
N° Page
Ouverture
p. 1-12
Thème 1 : Nombres et calculs
Testez le chapitre 100 % débloqué
Thème 2 : Organisation et gestion de données
Thème 3 : Grandeurs et mesures
Thème 4 : Espace et géométrie
Annexes
Nos dossiers d'actualité
Dossier d'actualité
/ 443
Vue papier
Animation montrant le basculement entre la vue numérique et la vue papier
Découvrez la vue papier en cliquant ici
Page précédente
Chapitre 1
Exercices

Exercices numériques

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
Tableur
Une première approche de la division euclidienne

Nous allons mettre en place une manière très simple de calculer les divisions euclidiennes à lʼaide dʼun tableur.
Aide
Sur le tableur, la fonction ENT(X) donne la partie entière du nombre X, cʼest-à-dire la partie de ce nombre qui est avant la virgule. Téléchargez le fichier ressource de l'exercice.
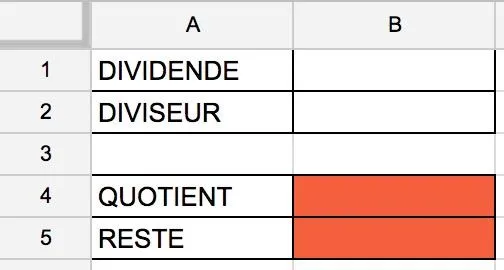
Placeholder pour Tableau illustrant une opération de division : dividende, diviseur, quotient et reste sont indiqués dans un tableau.Tableau illustrant une opération de division : dividende, diviseur, quotient et reste sont indiqués dans un tableau.
1. Sur le tableur, la fonction ENT(X) donne la partie entière du nombre X. a. Vérifiez à l'aide du tableur que ENT(1,23) = 1

b. Dans la cellule B4, entrez la formule qui permet dʼobtenir la partie entière de la division du dividende par le diviseur.

2. a. Si on connait le dividende, le diviseur et le quotient, comment trouver le reste dʼune division euclidienne ?

b. Dans la cellule B5, rentrez la formule qui permet dʼobtenir le reste de la division euclidienne du dividende par le diviseur.
3. À lʼaide du tableur, effectuez la division euclidienne de 24 par 7 et vérifiez que le quotient vaut 3 et le reste 3.

4. Trouvez le reste et le quotient dans la division euclidienne :
a. de 25 789 par 127 ;
b. de 114 536 par 834 ;
c. de 25 478 354 877 par 11 213.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

61
Scratch
Une nouvelle approche de la division euclidienne

Ici, nous allons mettre en place le véritable programme utilisé par les informaticiens pour connaitre le résultat dʼune division euclidienne. Téléchargez le fichier ressource de l'exercice.
1. Effectuez la division euclidienne de 126 par 14 à la main. Comment vous y prenez-vous ?
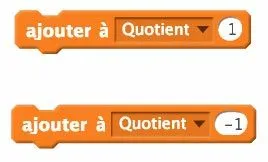
2. La première étape est de construire une boucle pour regarder si le quotient vaut 0 ; 1 ; 2… Parmi les deux propositions ci-dessous, laquelle vous semble la plus pertinente comme condition dʼarrêt de la boucle ? Placez-la dans le programme.
Placeholder pour Schéma: illustration de la division. Deux lignes montrent la relation entre le diviseur, le quotient et le dividende, avec les symboles > et <.Schéma: illustration de la division. Deux lignes montrent la relation entre le diviseur, le quotient et le dividende, avec les symboles > et <.
3. Vous pouvez remarquer quʼil y a un espace libre dans la boucle, et un autre après la boucle. Dans quel ordre faut-il placer les deux propositions ci-dessous pour que le programme fonctionne ? Quel est lʼintérêt de la seconde instruction ?
Placeholder pour Capture d'écran de deux blocs de code : incrémenter et décrémenter une variable nommée Quotient.Capture d'écran de deux blocs de code : incrémenter et décrémenter une variable nommée Quotient.
4. Testez votre programme sur les nombres suivants et comparez vos résultats avec ceux obtenus dans le premier exercice :
a. de 24 par 7 ;
b. de 25 789 par 127 ;
c. de 114 536 par 834 ;
d. de 25 478 354 877 par 11 213.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Version antérieure

Scratch : Une nouvelle approche de la division euclidienne
Placeholder pour Capture d'écran de deux blocs Scratch orange : l'un ajoute 1, l'autre soustrait 1 à la variable 'Quotient'.Capture d'écran de deux blocs Scratch orange : l'un ajoute 1, l'autre soustrait 1 à la variable 'Quotient'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Version antérieure

Scratch : Une nouvelle approche de la division euclidienne
Placeholder pour Capture d'écran Scratch : blocs comparant le produit du diviseur et du quotient au diviseur pour illustrer la division euclidienne.Capture d'écran Scratch : blocs comparant le produit du diviseur et du quotient au diviseur pour illustrer la division euclidienne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Exercice numérique

Amélie a écrit le programme ci-dessous en langage Scratch.
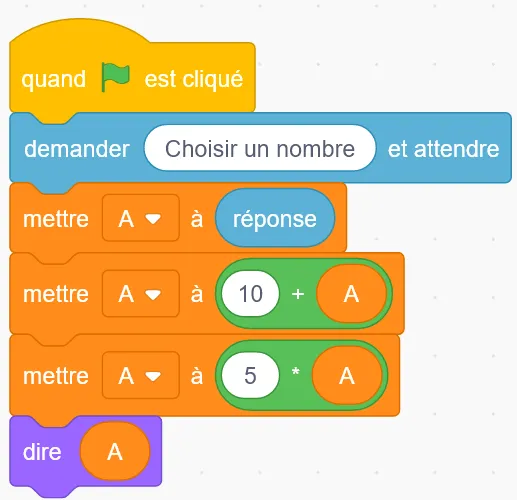
Placeholder pour Capture d'écran de code Scratch : script calculant un nombre saisi par l'utilisateur. Ce nombre est additionné à 10, puis multiplié par 5 avant affichage du résultat final.Capture d'écran de code Scratch : script calculant un nombre saisi par l'utilisateur. Ce nombre est additionné à 10, puis multiplié par 5 avant affichage du résultat final.

1. Elle souhaite réduire le nombre d'instructions. Proposer une solution.

2. Tester le programme avec les nombres 4 et 0,1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Exercice numérique

Julien a effectué des achats pour sa future rentrée scolaire.
Voici le bon de commande qu'il a obtenu :

Code de l'article Désignation Prix à l'unité Quantité Prix
37 123 Stylo 4 couleurs 1,95 3
58 787 24 crayons de couleur 3,85 1
24 478 24 feutres 5,99 2
12 589 Stylo plume 7,32 2
23 333 Gomme 0,31 4
Total

1. Reproduire le bon de commande dans une feuille de calcul.

2. Quelle formule faut-il entrer dans la cellule E3 pour permettre d'automatiser le calcul du prix jusqu'à la cellule E7 ?

3. Quelle formule faut-il entrer dans la cellule E8 ?

4. Compléter le tableur ci-dessus et donner le prix total.

Page suivante