Calcul
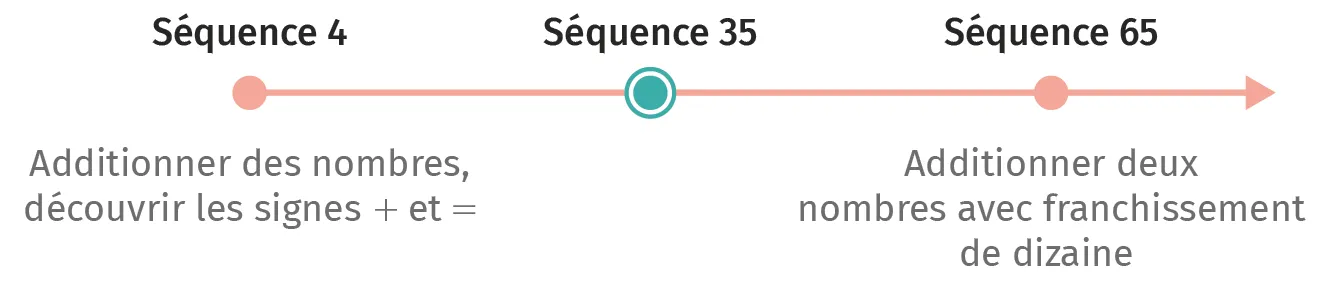
Séquence 35
Additionner deux nombres sans franchissement de dizaine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Calculer la somme de deux nombres
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans cette séquence, les élèves vont utiliser leurs connaissances en numération pour comprendre comment additionner deux nombres à deux chiffres qui ne nécessitent pas de créer une nouvelle dizaine. Utiliser les décompositions des nombres en dizaines et en unités permet de donner du sens aux procédures de calcul afin que les élèves les comprennent avant de pouvoir les automatiser.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
SÉANCE 1
60 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problèmes additifs : recherche d'une partie
Problème 1Lily a 20 rubans. 12 sont bleus et les autres sont jaunes.
Combien de rubans jaunes Lily a-t-elle ?
Retrouvez ce problème au format .
Problème 2
Kaïs et Lina ont 20 jouets à eux deux.
11 sont à Kaïs, combien sont à Lina ?
Retrouvez ce problème au format .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compléments à la dizaine supérieure
Énoncer un nombre. Les élèves écrivent sur leur ardoise le complément à la dizaine supérieure de ce nombre. Valider en faisant répéter aux élèves la décomposition et en dessinant les cubes au tableau. Répéter dix fois.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectifs de la séance
- Savoir calculer la somme de deux nombres à deux chiffres en utilisant du matériel
- Découvrir les arbres de calculs
Matériel
- Fichier élève p. 75
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Présentation de l'apprentissage de la séance
Collectif
2 min
Collectif
2 min
« Aujourd'hui, nous allons continuer notre travail pour apprendre à ajouter des nombres. Nous allons apprendre à additionner deux nombres qui s'écrivent avec deux chiffres. »


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Ajouter deux nombres : recherche à deux
Individuel puis en binômes
10 min
Écrire « 23 + 14 » au tableau et demander aux élèves d'essayer d'effectuer individuellement ce calcul sur leur ardoise, puis de comparer leur procédure et leur résultat avec leur voisin, et de se mettre d'accord sur une réponse.
Individuel puis en binômes
10 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Mise en commun des procédures des élèves
Collectif
10 min
Organiser une mise en commun au cours de laquelle les élèves présentent leurs procédures. Ils pourraient dire : Collectif
10 min
Nous avons compté 14 à partir de 23 sur la droite graduée. Nous sommes arrivés à 37.
Nous savons que 14, c'est 10 + 4. Nous avons fait 23 + 10 = 33, puis 33 + 4 = 37.
Il y a 2 dizaines dans 23 et 1 dizaine dans 14, cela fait donc 3 dizaines. Il y a 3 + 4 unités restantes, ce qui fait 7.
Le résultat a 3 dizaines et 7 unités : c'est 37.
Le résultat a 3 dizaines et 7 unités : c'est 37.
Lors de cette mise en commun, il est important d'aider les élèves à verbaliser leur procédure en prenant appui sur leur ardoise, et de reformuler pour permettre à tous de comprendre le calcul effectué.
Expliquer aux élèves que surcompter sur la droite graduée permet de trouver le résultat correct, mais que cette procédure prend de plus en plus de temps à mesure qu'on travaille avec des grands nombres et qu'il y a un risque d'erreur.
Utiliser les décompositions des nombres pour effectuer l'addition.

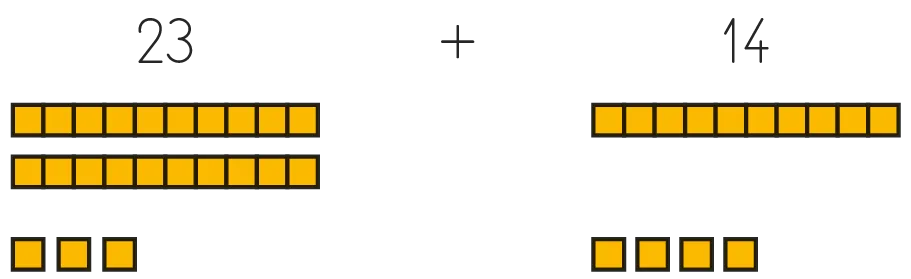
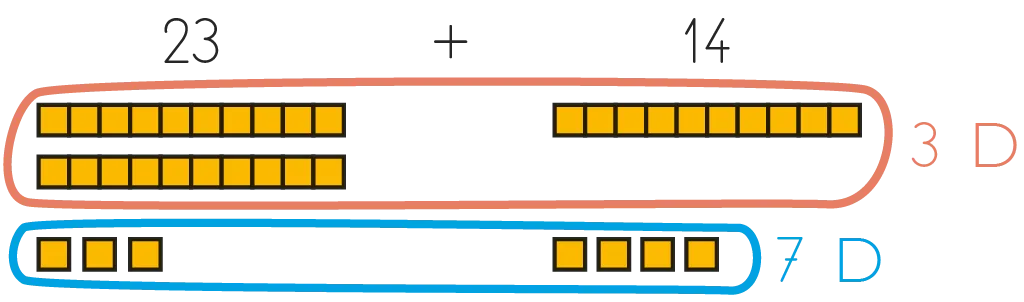
« Dans 23, il y a 3 unités, et dans 14, il y en a 4. Cela fait donc 7 unités en tout : il n'y a pas de nouvelle dizaine à constituer. Il y a 2 dizaines dans 23 et 1 dans 14 : le résultat comporte alors 3 dizaines. 23 + 14, cela fait donc 3 dizaines et 7 unités, c'est-à-dire 37. En nous appuyant sur les dizaines et les unités, on peut trouver le résultat de ce calcul. »

Expliquer ensuite aux élèves que l'on peut aussi présenter son calcul sous la forme d'un « arbre ».
« Quand j'ai calculé, j'ai regroupé les dizaines avec les dizaines et les unités avec les unités. Je peux le faire sans dessiner les cubes. Je calcule d'abord combien il y a d'unités pour être sûr qu'il n'y a pas de nouvelle dizaine à constituer. Pour écrire mon résultat, je trace des traits qui partent des unités et qui se rejoignent en dessous. 3 + 4 = 7. J'écris 7 là où les traits se rejoignent.

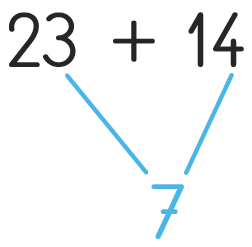

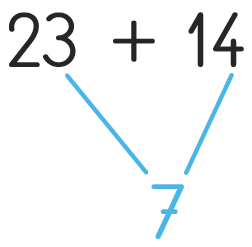
Ensuite, je cherche combien il y a de dizaines et je l'écris de la même façon. 2 + 1 = 3.

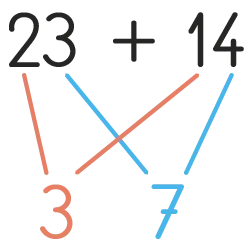 3 dizaines et 7 unités, c'est 37. »
3 dizaines et 7 unités, c'est 37. »

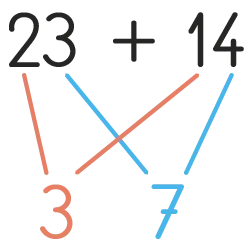
Proposer aux élèves de chercher collectivement le résultat de 32 + 24 en s'appuyant sur les dizaines et les unités. Représenter les nombres à l'aide des dizaines et des unités, puis écrire le calcul sous la forme d'un arbre, et indiquer le résultat.
Organiser un temps d'entrainement en binômes en demandant aux élèves d'effectuer les calculs suivants : 26 + 23 ; 31 + 14 et 35 + 24.
Différenciation
• Laisser les élèves qui en éprouvent le besoin utiliser librement le matériel de numération.
• Proposer aux élèves à l'aise d'inventer un calcul et de l'effectuer. Leur demander de faire valider leur calcul au préalable afin qu'ils n'aient pas de retenue.
• Proposer aux élèves à l'aise d'inventer un calcul et de l'effectuer. Leur demander de faire valider leur calcul au préalable afin qu'ils n'aient pas de retenue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4 Entrainement individuel sur le fichier
Individuel15 min
Projeter la page 75 du fichier et donner les consignes.
Individuel
15 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Bilan
Collectif3 min
Collectif
3 min
- Bilan de l'activité « Si vous avez réussi à ajouter deux nombres qui s'écrivent avec deux chiffres, levez le pouce sur le cœur. »
- Bilan mathématique Écrire « 45 + 32 » et demander aux élèves de montrer avec leurs doigts combien le résultat aura d'unités restantes. « 45 a 5 unités restantes et 32 en a 2. 5 + 2 = 7, il y aura donc 7 unités non groupées dans le résultat. »
- Bilan métacognitif Demander aux élèves d'échanger à deux sur ce qu'ils ont appris.
- Synthèse en revenant à la cible « Vous savez maintenant ajouter deux nombres en utilisant leur décomposition en dizaines et en unités. »
Procéder de la même manière avec les dizaines. Conclure en énonçant le résultat du calcul.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

