Nos classiques

Guide CP-Maths

I
Présentation
II
Liaison grande section - CP
Période 1
Période 2
Période 3
27- Découvrir les euros
Grandeurs et mesuresp. 132-133
28- Suite orale des nombres jusqu'à 59
Numérationp. 134-136
29- Table d'addition : les doubles
Calculp. 137-139
30- Découvrir les mètres et les centimètres, mesurer des segments
Grandeurs et mesuresp. 140-142
31- Dizaines-unités : commander des collections jusqu’à 99
Numérationp. 143-146
32- Construire et décrire le cube et le pavé
Géométriep. 147-149
33- Les compléments à la dizaine supérieure
Calculp. 150-152
34- Utiliser la monnaie pour comprendre la relation dizaines-unités
Grandeurs et mesuresp. 153-154
35- Additionner deux nombres sans franchissement de dizaine
Calculp. 155-156
36- Suite écrite des nombres jusqu’à 100
Numérationp. 157-158
37- Comparer et ordonner des nombres jusqu’à 100
Numérationp. 159-160
38- Coder un déplacement dans la classe
Géométriep. 161-163
39- Soustraire un nombre inférieur à 10
Calculp. 164-166
40- La grande enquête : le tableau de données
Organisation et gestion de donnéesp. 167-169
Problèmes additifs à deux étapes
Problèmesp. 170-172
Problèmes multiplicatifs : recherche du produit
Problèmesp. 173-175
Problèmes en plein air
Problèmesp. 176-177
Période 4
Période 5
Annexes
Calcul
39

Soustraire un nombre inférieur à 10

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour Schéma linéaire : apprentissage de la soustraction. Découverte (séquence 15), soustraction de nombres (23), étape finale (39).Schéma linéaire : apprentissage de la soustraction. Découverte (séquence 15), soustraction de nombres (23), étape finale (39).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Objectif de la séquence

  • Mettre en œuvre des procédures pour soustraire un nombre inférieur à 10 à un nombre inférieur à 20
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Conseil didactique

Dans les séquences précédentes, les élèves ont découvert différents sens de la soustraction et effectué des soustractions avec des nombres inférieurs à 10. Dans cette séquence, ils vont soustraire des nombres inférieurs à 10 à des nombres jusqu'à 20. Bien qu'ils aient déjà travaillé sur des calculs tels que ceux-ci en résolution de problème, cette séquence a pour but de fixer les procédures de calcul efficaces qui peuvent être réutilisables dans des calculs plus complexes. Les élèves vont ainsi commencer à raisonner sur les nombres pour utiliser la procédure de calcul la plus adaptée en fonction des nombres en jeu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 1
60 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Rituel de numération
Collectif
10 min

Combien de dizaines, combien d'unités ?

Utiliser l'outil « Dizaines-unités ». Présenter de façon aléatoire des collections avec une ou deux dizaines cachées. Les élèves écrivent sur leur ardoise combien il y a de dizaines et d'unités. Répéter cinq fois.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Rituel de calcul
Collectif
10 min

Additions sans franchissement de dizaine

Énoncer une addition qui ne fait pas intervenir de franchissement de dizaine. Les élèves écrivent le calcul et son résultat sur leur ardoise. Valider en écrivant l'addition au tableau. Répéter dix fois.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Apprentissage
40 min

Objectif de la séance
  • Soustraire en utilisant le passage par 10
Matériel
  • Fichier élève p. 79
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Rappel du travail déjà effectué sur la soustraction
Collectif
2 min

Demander aux élèves de rappeler le travail réalisé avec les tours de cubes sur la soustraction.
« Aujourd'hui, nous allons poursuivre notre travail sur la soustraction. Nous allons apprendre à effectuer des soustractions en utilisant les décompositions des nombres. »
Placeholder pour Illustration : étoile jaune souriante tenant une cible avec une flèche au centre.Illustration : étoile jaune souriante tenant une cible avec une flèche au centre.
Effectuer des soustractions en utilisant les décompositions des nombres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Problème soustractif
Individuel
10 min

Poser le problème suivant aux élèves : « Il y avait 17 oiseaux dans l'arbre. 5 se sont envolés. Combien reste-t-il d'oiseaux dans l'arbre ? »
Faire reformuler le problème par un ou plusieurs élèves pour s'assurer de la compréhension du problème par tous.
Différenciation
Proposer si besoin une décomposition chronologique de l'histoire pour aider les élèves à reformuler : avant, ensuite, à la fin.
Proposer une situation déjà rencontrée par les élèves permet de s'assurer de la compréhension du problème par tous. Les élèves peuvent ainsi se concentrer sur les procédures de calcul.
Demander aux élèves de réfléchir quelques minutes individuellement, puis de résoudre ce problème à deux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Soustraire en utilisant les décompositions des nombres
Collectif
10 min

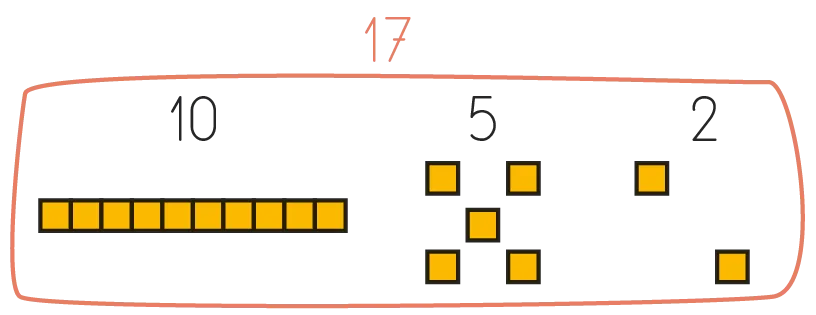
Mettre en commun les réponses des élèves et se mettre d'accord sur le calcul « 17-5 ».
Demander aux élèves d'expliquer comment ils ont trouvé le résultat. Les élèves pourraient dire :
Nous avons placé 17 sur la droite graduée et nous avons reculé de 5. Nous sommes arrivés sur 12.

Nous avons utilisé nos doigts : 16 ; 15 ; 14 ; 13 ; 12.

Nous avons dessiné 17 ronds et nous en avons barré 5. Il en restait 12.

Expliquer aux élèves que l'on peut utiliser nos connaissances sur les nombres pour effectuer des soustractions.
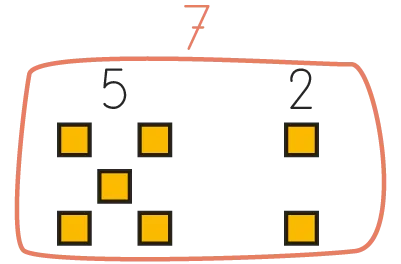
« Ici, nous cherchons à calculer 17 - 5. Nous savons que 7 - 5 = 2. Nous allons utiliser cette décomposition pour effectuer notre soustraction. »
Représenter au tableau la relation entre 5, 2 et 7 avec les cubes.
Placeholder pour Schéma: sept carrés jaunes, cinq à gauche et deux à droite, totalisant 7.Schéma: sept carrés jaunes, cinq à gauche et deux à droite, totalisant 7.
« Nous ajoutons une dizaine à 7 pour obtenir 17.
Placeholder pour Illustration du nombre 17 décomposé : 10 carrés jaunes alignés et 7 carrés jaunes en quinconce.Illustration du nombre 17 décomposé : 10 carrés jaunes alignés et 7 carrés jaunes en quinconce.
17, c'est 10 + 7. Comme nous savons que 7 - 5 = 2, nous pouvons comprendre que 17 - 5 = 12. Nous enlevons des unités mais la dizaine reste entière. »
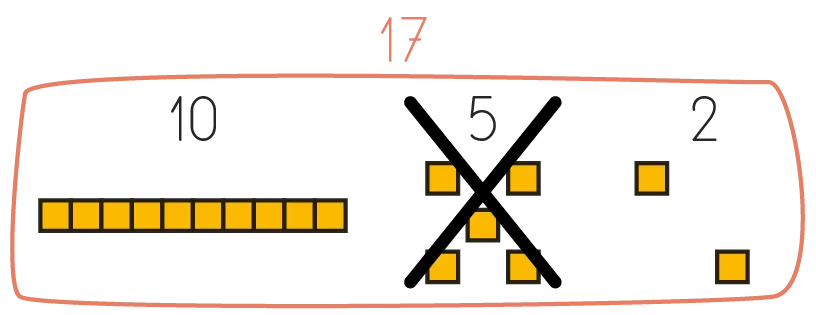
Barrer 5 unités sur le schéma et écrire « 17 - 5 = 12 ».
Placeholder pour Illustration: calcul de soustraction 17 - 5 = 12. Représentation visuelle avec des carrés jaunes.Illustration: calcul de soustraction 17 - 5 = 12. Représentation visuelle avec des carrés jaunes.
Écrire « 18 - 4 » au tableau et demander aux élèves de chercher le résultat sur leur ardoise.
Mettre en commun en verbalisant la procédure consistant à utiliser les décompositions des nombres.
« J'utilise les relations que je connais entre les nombres pour calculer 18 - 4. 4 + 4 = 8, donc 8 - 4 = 4. Cela veut dire que 18 - 4 = 14. »
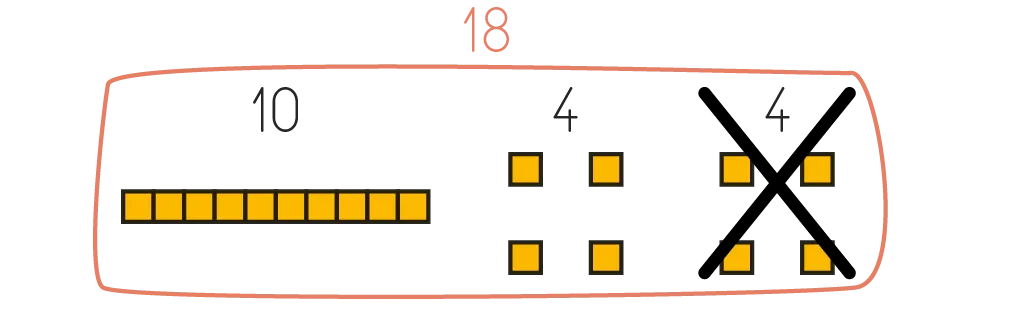
Placeholder pour Schéma de soustraction : 18 - 4 = 14. Illustration avec des carrés jaunes.Schéma de soustraction : 18 - 4 = 14. Illustration avec des carrés jaunes.
Proposer ensuite aux élèves de calculer 16 - 3 puis 18 - 5 et procéder de la même manière.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Entrainement individuel sur le fichier
Individuel
15 min

Projeter la page 79 du fichier et donner les consignes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Bilan
Collectif
3 min

  • Bilan de l'activité
    « Si vous avez réussi à utiliser les décompositions des nombres pour effectuer des soustractions, levez le pouce sur le cœur. »

  • Bilan mathématique
    Écrire « 16 - 4 » au tableau et demander aux élèves de trouver quelle décomposition utiliser pour trouver le résultat. « Nous savons que 4 + 2 = 6, donc 6 - 4 = 2. Nous ajoutons une dizaine à 6 pour obtenir 16 : 16-4 = 12. On met la dizaine de côté, et on soustrait 4 aux unités. »
    Représenter la soustraction avec des cubes
  • Bilan métacognitif
    Demander aux élèves d'échanger à deux sur ce qu'ils ont appris.
  • Synthèse en revenant à la cible
    « Nous avons appris à utiliser nos connaissances sur les nombres pour effectuer des soustractions. Nous avons utilisé les décompositions des nombres pour trouver le résultat des soustractions. »

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.