Les moitiés des nombres inférieurs à 20

• Comprendre la notion de moitié
• Découvrir les moitiés des nombres inférieurs à 20

Les élèves ont découvert les doubles dans la séquence 29. Dans cette séquence, ils vont découvrir les moitiés des nombres jusqu'à 20 grâce à la notion de partage équitable, et faire le lien avec les doubles.

Additions sans franchissement de dizaine

Énoncer une addition qui ne fait pas intervenir de franchissement de dizaine. Les élèves écrivent le calcul et son résultat sur leur ardoise. Valider en explicitant les étapes au tableau. Répéter cinq fois.

1

Rappel sur les doubles

Collectif

2 min

Demander aux élèves de rappeler ce que sont les doubles.
« Nous avons travaillé sur les doubles. Chercher le double d'un nombre, c'est faire la somme des deux mêmes nombres. Aujourd'hui, nous allons découvrir les moitiés. »

2

Découverte des moitiés

En binômes

5 min

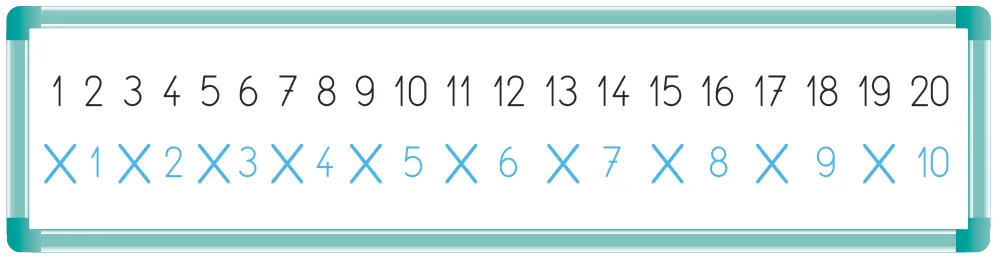
Écrire les nombres jusqu'à 20 en haut du tableau. « Je vais donner 20 jetons à chaque binôme : vous allez les partager entre vous pour que chacun ait le même nombre de jetons. »
Distribuer 20 jetons par binôme et les laisser les partager. Organiser une mise en commun en demandant aux élèves s'ils ont réussi à partager les jetons en deux parts égales. Expliquer : « Vous avez partagé 20 jetons entre vous et chacun a eu 10 jetons. On dit que 10, c'est la moitié de 20. »
Écrire « 10 » sous le nombre 20. Procéder de la même manière avec 19 jetons.
Lors de la mise en commun, montrer aux élèves qu'ils ne peuvent pas partager tous les jetons : chaque élève a 9 jetons, et il reste 1 jeton. « On ne peut pas partager 19 jetons en deux parts égales sans casser de jeton. »
Dessiner une croix sous le nombre 19.

3

Recherche à deux

En binômes

10 min

Demander aux élèves de chercher les quantités que l'on peut partager en deux de façon équitable, c'est-à-dire en ayant chacun une moitié.
Pour cela, les élèves piochent une carte, préparent la collection de jetons correspondante et essaient de la partager. Puis, ils écrivent le résultat sur leur cahier de recherche, comme au tableau : le nombre de jetons, la moitié si le partage équitable en deux est possible, ou dessinent une croix si ce n'est pas possible.

4

Mise en commun

Collectif

5 min

Mettre en commun les résultats trouvés par les élèves en écrivant les moitiés trouvées ou non au tableau.
Expliquer que lorsqu'on peut partager une quantité en deux quantités égales, chaque quantité est la moitié de la quantité initiale. « La moitié de 10, c'est 5, car quand on partage 10 en deux quantités égales, on trouve 5. »
Dessiner deux constellations de 5 jetons et dire : « 5 + 5 = 10 : 10 est le double de 5, et 5 est la moitié de 10. »

5

Entrainement individuel sur le fichier

Individuel

15 min

Projeter la page 90 du fichier et donner les consignes.

6

Bilan

Collectif

3 min

• Bilan de l'activité
« Si vous avez réussi à trouver des moitiés, levez le pouce sur le cœur. »


• Bilan mathématique
Dessiner 16 jetons au tableau et demander aux élèves de montrer la moitié avec leurs doigts. Faire venir deux élèves montrant chacun 8 doigts et dire « Chaque élève lève 8 doigts : 8, c'est la moitié de 16. 8+ 8 = 16. »


• Bilan métacognitif
Demander aux élèves d'échanger à deux sur ce qu'ils ont appris.


• Synthèse en revenant à la cible
« Nous avons découvert les moitiés : chercher la moitié, c'est partager une quantité en deux quantités égales. On dit que la moitié de 10, c'est 5. Nous savons déjà que 5+ 5 = 10. On peut donc dire que 10 est le double de 5 et que 5 est la moitié de 10. »