Les doubles et les moitiés des dizaines entières

• Calculer les doubles des dizaines entières et les moitiés de 20, 40, 60, 80 et 100

Les élèves ont découvert la notion de double et de moitié, et ils se sont entrai-nés à mémoriser les doubles des nombres jusqu'à 10 et des moitiés des nombres inférieurs à 20. Dans cette séquence, il s'agit de travailler les procédures de calcul et de permettre aux élèves de faire le lien avec leurs connaissances en numération. Ainsi, on fera comprendre aux élèves que pour trouver le double ou la moitié de dizaines entières, on utilise les faits numé-riques mémorisés que sont les doubles et les moitiés.

Problèmes additifs : recherche d'une partie

Problème 1
Il y avait 9 pommes sur la table. Nous en avons mangé 3.
Combien de pommes y a-t-il maintenant ?
Retrouvez ce problème au format

numérique

.

Problème 2
Antoine a donné 9 de ses 20 images d'animaux à sa sœur.
Combien lui reste-t-il d'images ?
Retrouvez ce problème au format

numérique

.

Procédures de calculs du CP : test de fluence n ° 6 p. 157

Ce test de fluence porte sur les procédures de calcul apprises jusqu'ici.
Les élèves ont 3 minutes pour réaliser le plus de calculs possible, l'objectif de fin d'année étant de neuf. Pour ce test, procéder de la même manière que pour les précédents (explications p. 56).

1

Rappel : les doubles et les moitiés

Collectif

2 min

Demander aux élèves d'écrire sur leur ardoise le double de 10 puis la moitié de 20. Représenter 20 au tableau pour donner à voir aux élèves le lien entre double et moitié. Une trace de ce type pourra être conservée en affichage de référence pour la classe.
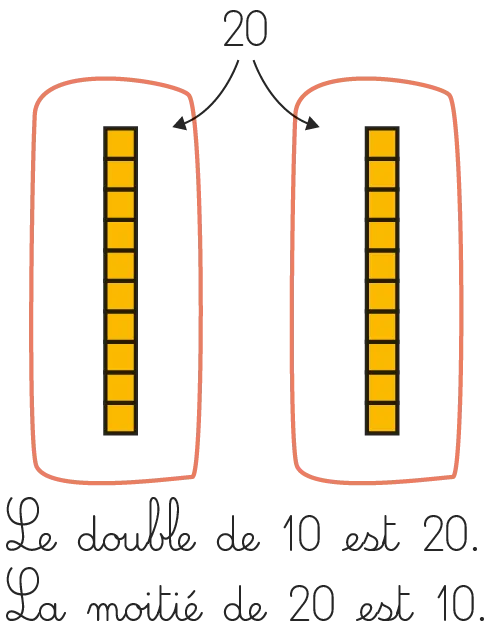
« Nous avons découvert les doubles et les moitiés. Aujourd'hui, nous allons apprendre à calculer les doubles et les moitiés des dizaines entières.  »

2

Les doubles des dizaines entières

En binômes puis collectif

10 min

Demander aux élèves de chercher le double de 30, en utilisant le matériel de numération s'ils le souhaitent. Après quelques minutes, organiser une mise en commun : « Calculer le double d'un nombre, c'est faire la somme des deux mêmes nombres. Ici, chercher le double de 30, c'est chercher le résultat de 30 + 30, c'est-à-dire 3 dizaines et encore 3 dizaines. »
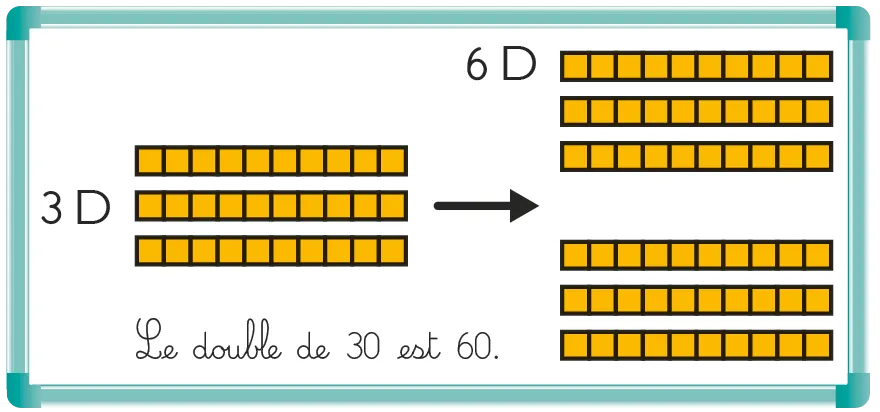
Écrire les dizaines entières au tableau sous la forme de … D et demander aux élèves de chercher en binômes les doubles de ces dizaines avec leurs dizaines détachables et d'écrire les résultats trouvés dans leur cahier de recherche.


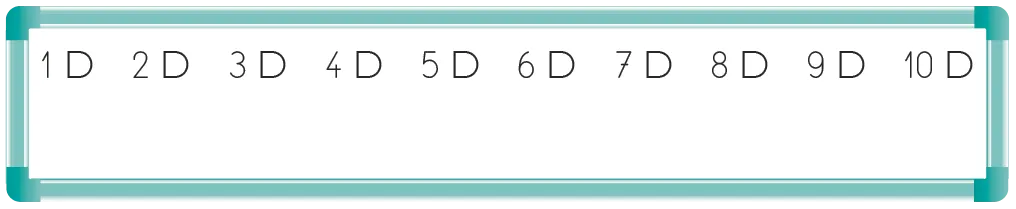
À l'issue de la phase de recherche, écrire au tableau les résultats trouvés par les élèves.


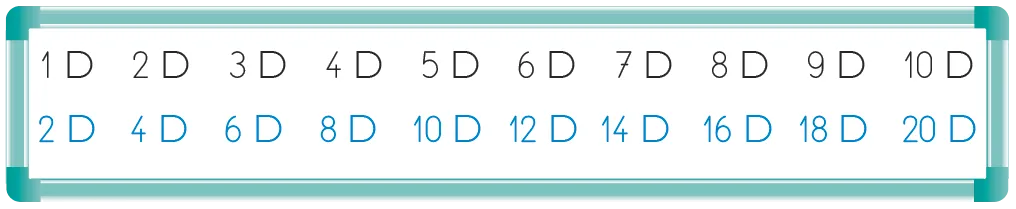
Expliciter collectivement  : « Pour trouver le double d'un nombre entier de dizaines, on s'appuie sur nos connaissances des doubles jusqu'à 10. Je cherche par exemple le double de 2 dizaines. Je sais que le double de 2, c'est 4 : le double de 2 dizaines, c'est alors 4 dizaines. Le double de 20, c'est donc 40.  »

3

Les moitiés

En binômes puis collectif

10 min

Effacer le bas du tableau mais conserver les résultats trouvés lors de l'étape précédente. Expliquer aux élèves : « Nous allons maintenant travailler sur les moitiés. Avec votre voisin, vous allez constituer les nombres écrits au tableau avec vos dizaines, puis vous allez les partager entre vous de façon équitable pour trouver la moitié. Vous écrirez sur votre cahier de recherche le nombre de départ, puis la moitié de ce nombre. S'il n'est pas possible de partager en deux parts équitables, vous tracez une croix sur votre cahier de recherche.  »
Mettre en commun les résultats trouvés et montrer aux élèves que les résultats étaient déjà disponibles au tableau Dessiner des flèches et écrire « moitié » pour montrer aux élèves le lien entre double et moitié.


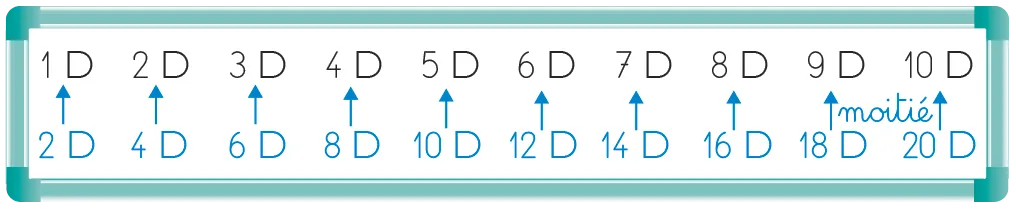
Expliquer  : « Chercher la moitié d'un nombre entier de dizaines, c'est partager en deux parts égales ce nombre de dizaines. À nouveau, on s'appuie sur nos connaissances. Je cherche par exemple la moitié de 4 dizaines. La moitié de 4 dizaines, c'est 2 dizaines. En effet, je sais que 2 + 2 = 4. Donc la moitié de 40, c'est 20.  »

4

Entrainement individuel sur le fichier

Individuel

15 min

Projeter la page 91 du fichier et donner les consignes.

5

Bilan

Collectif

3 min

• Bilan de l'activité
« Si vous avez réussi à trouver les doubles et les moitiés des dizaines entières, levez le pouce sur le cœur. »


• Bilan mathématique
Utiliser l'outil « Décomposition » pour afficher 6 dizaines au tableau et demander aux élèves de trouver la moitié. Puis, leur demander d'indiquer le double de 30. « Je sais que 60, c'est 6 dizaines. Pour trouver la moitié de 60, je cherche donc la moitié de 6 dizaines : la moitié de 6, c'est 3. En effet, 3 + 3 = 6. La moitié de 60, c'est donc 3 dizaines, c'est-à-dire 30. »


• Bilan métacognitif
Demander aux élèves d'échanger à deux sur ce qu'ils ont appris.


• Synthèse en revenant à la cible
« Nous avons appris à trouver les doubles et les moitiés des dizaines entières. Pour cela, nous utilisons nos connaissances en numération et nos connaissances sur les doubles et les moitiés. »