Calcul
Séquence 51
Les moitiés des nombres pairs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Calculer les moitiés des nombres pairs
- Connaitre la notion de nombre pair
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les élèves ont découvert et mémorisé les doubles et les moitiés des nombres inférieurs à 20. Ils ont également appris à trouver la moitié des dizaines entières. Dans cette séquence, ils vont découvrir les nombres pairs et impairs grâce à la notion de partage équitable et vont étendre leurs connaissances à la recherche de la moitié des nombres pairs. Cette procédure de calcul étant complexe pour des élèves de CP, les nombres proposés comportent tous un nombre pair de dizaines, afin de permettre aux élèves d'utiliser les moitiés qu'ils ont déjà mémorisées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
SÉANCE 1
60 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problèmes multiplicatifs : recherche de la valeur d'une part
Problème 1Justine distribue les 21 cartes d'un jeu à 3 joueurs. Combien de cartes chaque joueur aura-t-il ?
Retrouvez ce problème aux formats et .
Problème 2
Sasha a 20 cubes identiques et souhaite faire 2 tours de cubes de même hauteur en utilisant tous ses cubes.
Combien de cubes y aura-t-il dans chaque tour ?
Retrouvez ce problème au format .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Moitiés des nombres pairs jusqu'à 20
Écrire un nombre pair inférieur à 20 au tableau. Les élèves écrivent sa moitié sur leur ardoise. Vérifier collectivement avec le matériel de numération. Répéter dix fois.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectifs de la séance
- Calculer les moitiés des nombres pairs
- Comprendre la notion de nombre pair
Matériel de la séance
- Des cubes emboitables, à disposition
- 10 dizaines et 10 unités par binôme (matériel détachable)
- Fichier élève p. 99
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Entrée dans l'activité
Collectif
2 min
Demander aux élèves d'expliquer ce que sont les moitiés. Collectif
2 min
« Trouver la moitié d'un nombre, c'est partager la quantité en deux parties égales. Nous avons appris à calculer les moitiés des nombres jusqu'à 20 et de certaines dizaines entières. Aujourd'hui, nous allons apprendre à calculer les moitiés de plus de nombres. »


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Chercher la moitié d'un nombre
En binômes puis Collectif
10 min
Proposer aux élèves de revoir les moitiés des nombres jusqu'à 20 en s'entrainant en binômes : « Un élève écrit sur son ardoise un nombre entre 1 et 20 et son voisin doit trouver la moitié de ce nombre. Si on ne peut pas partager la quantité en deux parts équitables, on trace une croix. Puis on change les rôles. »En binômes puis Collectif
10 min
Après quelques minutes, organiser une mise en commun en listant au tableau avec les élèves les nombres compris entre 1 et 20 dont on peut trouver la moitié.








Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Chercher la moitié d'un nombre
Collectif
10 min
Expliquer aux élèves qu'ils vont devoir chercher la moitié de 24 en s'aidant des dizaines et des unités. Les laisser chercher puis organiser une mise en commun au tableau. Collectif
10 min
« On cherche la moitié de 24. 24, c'est 2 dizaines et 4 unités. Je partage les 2 dizaines : ça fait 1 dizaine chacun. Puis je partage les 4 unités : cela fait 2 unités chacun. Chaque élève a donc 12 cubes. On peut vérifier en faisant 12 + 12 = 24. 12 est la moitié de 24 et 24 est le double de 12. »

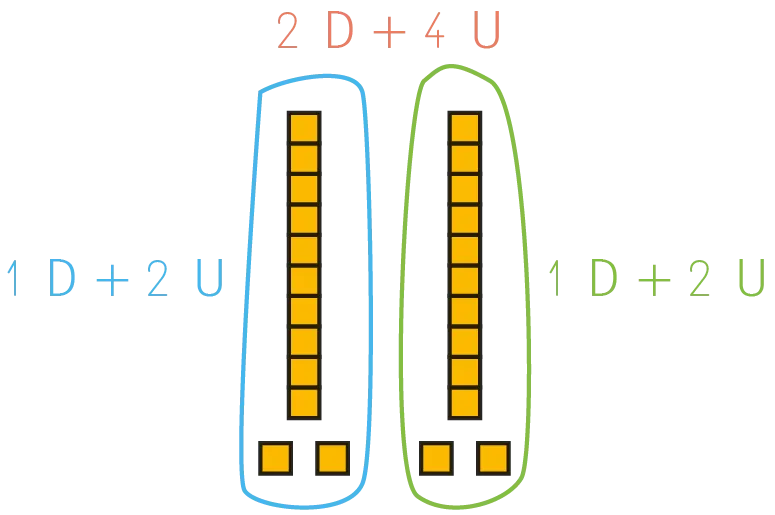
Expliquer que l'on peut trouver la moitié de 64 sans utiliser les cubes, en décomposant 64 puis en cherchant la moitié des dizaines et la moitié des unités.

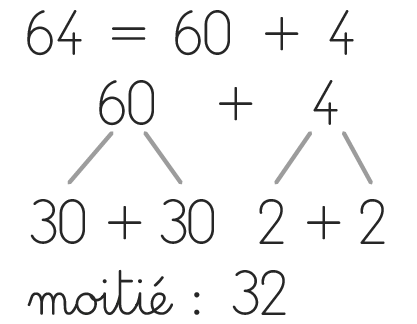

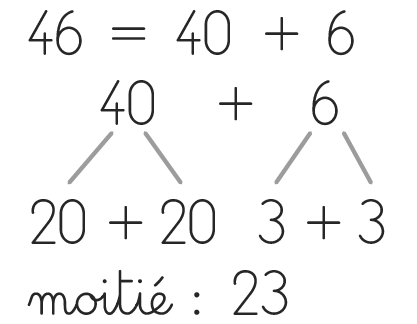
Organiser une mise en commun : « On ne peut pas partager 25 en deux parties égales sans casser de cube : chacun a 12 cubes et il reste 1 cube. 12 + 12 + 1 = 25.

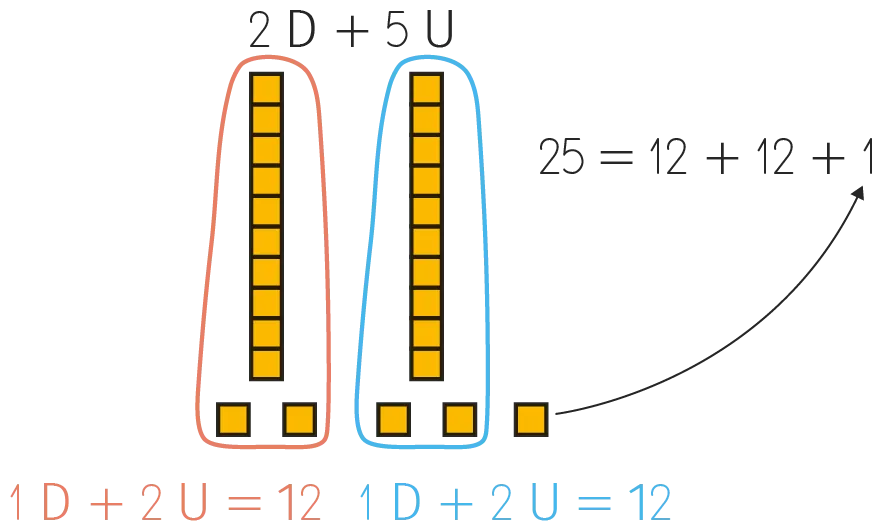
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4 Entrainement individuel sur le fichier
Individuel15 min
Projeter la page 99 du fichier et donner les consignes.
Individuel
15 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Bilan
Collectif3 min
Collectif
3 min
- Bilan de l'activité « Si vous avez réussi à trouver des moitiés, levez le pouce sur le cœur. »
- Bilan mathématique Demander aux élèves de trouver la moitié de 28. Valider en utilisant un arbre de calcul. « Ce nombre est pair car il a 8 unités restantes : on sait donc calculer sa moitié. 14 + 14 = 28. 14 est la moitié de 28 et 28 est le double de 14. »
- Bilan métacognitif Demander aux élèves d'échanger à deux sur ce qu'ils ont appris.
- Synthèse en revenant à la cible « Nous avons appris à trouver la moitié des nombres pairs. Les nombres pairs sont les nombres que l'on peut partager en deux parties égales, sans avoir de reste. Ce sont les nombres qui ont 0, 2, 4, 6 ou 8 unités restantes. »

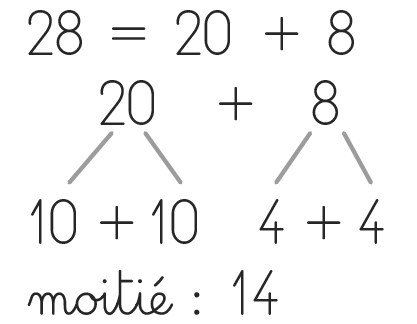
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

