Calcul
Séquence 56
Table d'addition : les presque doubles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Savoir reconnaitre les presque doubles
- Utiliser les doubles pour effectuer des calculs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Depuis la séquence 33, les élèves apprennent qu'ils peuvent utiliser les résultats mémorisés pour mettre en œuvre des procédures de calcul moins coûteuses. C'est à nouveau le cas dans cette séquence : les élèves vont être amenés à « chercher des doubles » , c'est-à-dire transformer des calculs pour les effectuer rapidement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Séance 1
55 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Représenter des nombres
Énoncer un nombre. Les élèves doivent le représenter de différentes manières sur leur ardoise. Mettre en commun les propositions des élèves au tableau pour obtenir des représentations variées.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ajouter 9
Énoncer un calcul du type « 9+... » ou « ... + 9 ». Les élèves écrivent le calcul et son résultat sur leur ardoise. Valider collectivement et modéliser sur la droite graduée. Répéter cinq fois.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif de la séance
- Découvrir les presque doubles
Matériel
- Fichier élève p. 110
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Entrée dans l'activité
Collectif
2 min
« Aujourd'hui, nous allons découvrir les presque doubles. Ce sont des calculs qui sont très proches des doubles. »
Collectif
2 min


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Découverte du problème
Collectif
5 min
« Des enfants ont joué au jeu du lancer. Vous allez calculer
leur score. »Collectif
5 min
Projeter l'image « Jeu du lancer » et placer deux aimants sur la case 6.


Valider collectivement : « 6+ 6 = 12. Nous avons utilisé nos connaissances sur les doubles. »
Proposer un nouveau score à calculer en plaçant les aimants sur le 7.

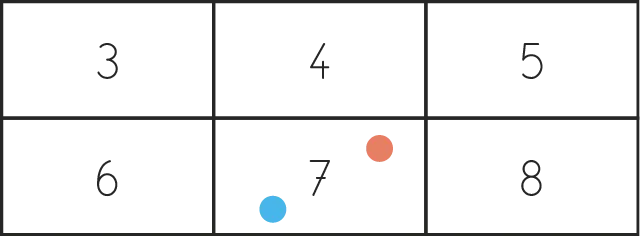
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Les presque doubles
Collectif
10 min
Proposer un nouveau score à calculer en plaçant un aimant sur 6 et un autre sur 7.
Collectif
10 min


Les élèves pourraient dire :
- Nous avons utilisé la droite graduée : nous sommes partis de 7 et nous avons avancé de 6. Nous sommes arrivés sur 13.
- Nous avons utilisé les doigts de nos quatre mains : 6 doigts et 7 doigts, ça fait 13 doigts.
- Nous avons dessiné des points : il y en a 13.
Projeter le diaporama « Constellations de points ».

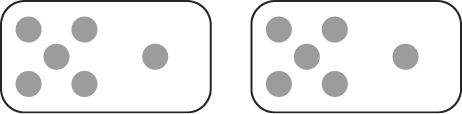
Afficher la seconde image du diaporama : 6 + 7.

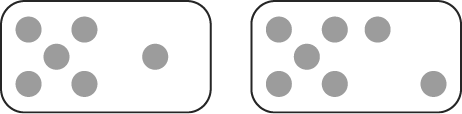


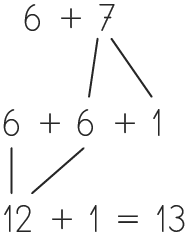
Utiliser la même méthode en s'appuyant sur 7 + 7 et en retranchant 1. Proposer aux élèves de calculer 7 + 8 en utilisant les doubles connus, puis mettre en commun de la même manière, à partir de 7 + 7 + 1 ou 8 + 8 - 1 en utilisant les constellations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4 Entrainement individuel sur le fichier
Individuel15 min
Projeter la page 110 du fichier et donner les consignes.
Individuel
15 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Bilan
Collectif3 min
Collectif
3 min
- Bilan de l'activité « Si vous avez réussi à trouver les doubles cachés, levez le pouce sur le cœur. »
- Bilan mathématique Demander aux élèves quels doubles on peut utiliser pour trouver le résultat de 4 + 5.
- Bilan métacognitif Demander aux élèves d'échanger à deux sur ce qu'ils ont appris.
- Synthèse en revenant à la cible « Nous avons appris à utiliser les doubles pour trouver le résultat des presque doubles. Nous allons poursuivre notre entrainement la prochaine fois pour essayer de trouver très vite les résultats des presque doubles. »
« 4 + 5, c'est presque comme 4 + 4. On utilise donc le double de 4, auquel on ajoute 1, car 5 c'est 1 de plus que 4. 4 + 4 + 1 = 9. On peut aussi utiliser 5 + 5 et retrancher 1 : 5 + 5 - 1 = 9. »
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

