D'après bac STD2A, Polynésie, juin 2019
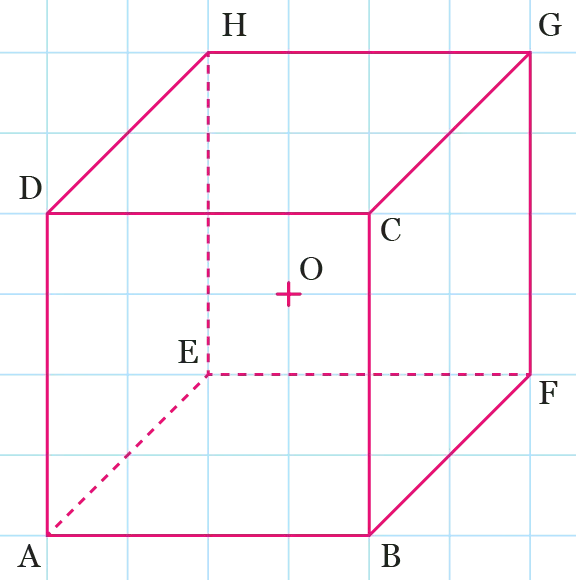
En 1982, l'architecte danois Johann Otto von Spreckelsen conçoit les plans de l'Arche de la Défense. Le monument parisien est représentée de manière simplifiée par un grand cube \text{A}'\text{B}'\text{C}'\text{D}'\text{E}'\text{F}'\text{G}'\text{H}' et un petit cube \text{ABCDEFGH} de même centre \text{O}, tels que le petit cube est une réduction de coefficient \dfrac{1}{2} du grand cube.

Reproduire au centre de la page le cube \text{ABCDEFGH} de côté 4 cm. On note \text{O} le centre du cube. Prévoir de la place autour du cube pour poursuivre la figure.

a) Placer le point \text{A}' tel que \overrightarrow{\mathrm{OA}'}=2 \overrightarrow{\mathrm{OA}}.
b) Placer le point \text{G'} tel que \overrightarrow{\mathrm{OG}'}=2 \overrightarrow{\mathrm{OG}}.
c) Justifier que les points \text{A}, \text{A}', \text{O}, \text{G} et \text{G}' sont alignés.

Construire de même les points \text{B}', \text{C}', \text{D}', \text{E}', \text{F}' et \text{H}'.

4

Soit \text{I}' le point défini par \overrightarrow{\mathrm{AI}'}=\frac{1}{4} \overrightarrow{\mathrm{A}' \mathrm{F}'}.
En considérant le triangle \text{A}'\text{G}'\text{F}', démontrer que \text{A}, \text{I}' et \text{D} sont alignés.

Aide

Penser au théorème de Thalès.

Soit t la translation de vecteur \overrightarrow{\text{AI}'}.
Construire les images respectives \text{J}, \text{K} et \text{L} de \text{B}, \text{F} et \text{E} par la translation t.

Plan de l'espace
a) Sélectionner l'icône Tétraèdre puis placer deux points non confondus dans le plan : le logiciel les nomme \text{A} et \text{B} et construit automatiquement le reste du tétraèdre \text{ABCD}.
b) Faire tourner la figure pour observer les différentes faces du tétraèdre.
c) Construire le point \text{E}, milieu de \text{[AB]}.
d) Construire le plan passant par les trois points \text{C}, \text{D} et \text{E}.

Droites de l'espace
a) Construire un point \text{F} appartenant à la face \text{ACD} du tétraèdre, puis la droite \text{(BF)}.
b) D'après la construction, quelle semble être la position relative (sécantes, parallèles, coplanaires, confondues, etc.) des droites \text{(BF)} et \text{(DE)} ?

Partie B

Ouvrir une nouvelle figure avec le logiciel GeoGebra et construire un cube \text{ABCDEFGH}.

a) Quelle semble être la position relative des plans \text{(ABC)} et \text{(EFG)} ?

b) Quelle semble être la position relative des plans \text{(EHD)} et \text{(EAD)} ?

a) Construire le plan \text{(FHD)}.
b) Que peut-on conjecturer sur la position des plans \text{(FHD)} et \text{(EFG)} ?

Partie C

On travaille sur la figure précédente.

Construire la droite \text{(EG)}.

2

a) Quelle semble être l'intersection de la droite \text{(EG)} et du plan \text{(FHD)} ?

b) Quelle semble être l'intersection de la droite \text{(EG)} et du plan \text{(EFG)} ?

c) Quelle semble être l'intersection de la droite \text{(EG)} et du plan \text{(ABC)} ?

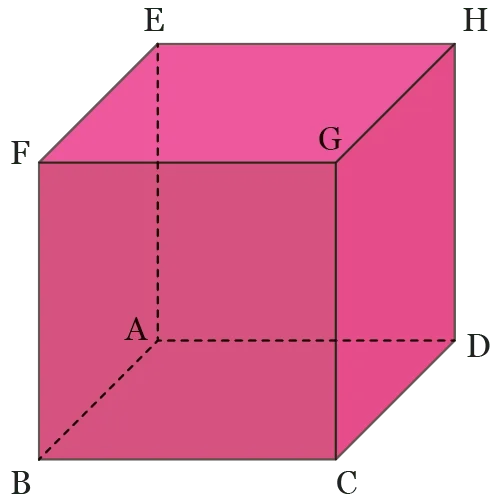
Soit \text{ABCDEFGH} le cube représenté ci-dessous.

Partie A : Coordonnées de vecteurs

1

Justifier que \text{A}, \text{B}, \text{D} et \text{E} ne sont pas coplanaires.

On dit alors que (\overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ) est une base de l'espace.

2

Déterminer les réels a, b et c tels que \overrightarrow{\mathrm{AC}}=a \overrightarrow{\mathrm{AB}}+b \overrightarrow{\mathrm{AD}}+c \overrightarrow{\mathrm{AE}}.

a, b et c sont les coordonnées du vecteur \overrightarrow{\text{AC}} dans la base (\overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ) et on les note \begin{pmatrix}a \\b \\c \end{pmatrix} ou ( a \ ; \ b \ ; \ c).

3

Déterminer les coordonnées des vecteurs \overrightarrow{\text{AF}}, \overrightarrow{\text{AG}}, \overrightarrow{\text{AH}} dans la base (\overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ).

Partie B : Coordonnées de points

On associe maintenant le point \text{A} à la base (\overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ) pour créer le repère de l'espace (\text{A} \ ; \ \overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ) défini par l'origine \text{A} et la base (\overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ).
On a \overrightarrow{\mathrm{AB}}=1 \overrightarrow{\mathrm{AB}}+0 \overrightarrow{\mathrm{AD}}+0 \overrightarrow{\mathrm{AE}} donc les coordonnées du point \text{B} sont (1 \ ; \ 0 \ ; \ 0) dans le repère (\text{A} \ ; \ \overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ).

1

Donner les coordonnées des points \text{A}, \text{D}, \text{E}, \text{C}, \text{F}, \text{G} et \text{H} dans le repère (\text{A} \ ; \ \overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ).

2

Soit \text{I} le milieu de \text{[CG]}. Exprimer \overrightarrow{\text{AI}} en fonction des vecteurs de la base puis en déduire les coordonnées de \text{I} dans la base (\text{A} \ ; \ \overrightarrow{\text{AB}} \ , \ \overrightarrow{\text{AD}} \ , \ \overrightarrow{\text{AE}} ).