Chapitre 2
Vecteurs, droites et plans de l'espace
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Capacités attendues
1. Représenter des combinaisons linéaires de vecteurs. 2. Décrire la position relative de droites et de plans.
3. Déterminer une base d'un plan ou de l'espace.
4. Lire sur une figure la décomposition de vecteurs dans une base.
5. Étudier des problèmes de configurations dans l'espace (alignement, parallélisme, coplanarité).
6. Déterminer une représentation paramétrique d'une droite.
7. Reconnaître une droite donnée par une représentation paramétrique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La Philharmonie de l'Elbe, qui se trouve à Hambourg en Allemagne, est une salle de concert conçue par les architectes Jacques Herzog et Pierre de Meuron.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Avant de commencer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Prérequis
1. Connaître les solides usuels.
2. Construire l'image d'un point par une translation.
3. Savoir utiliser les vecteurs du plan.
4. Démontrer que deux droites sont parallèles.
5. Déterminer les coordonnées d'un point défini par une relation vectorielle.
6. Démontrer que des points sont alignés.
7. Résoudre un système linéaire.
2. Construire l'image d'un point par une translation.
3. Savoir utiliser les vecteurs du plan.
4. Démontrer que deux droites sont parallèles.
5. Déterminer les coordonnées d'un point défini par une relation vectorielle.
6. Démontrer que des points sont alignés.
7. Résoudre un système linéaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Le philosophe et
mathématicien René
Descartes (1596-1650) est
l'un des fondateurs de
la géométrie analytique.
D'après ce qu'il rapporte
lui-même, il aurait trouvé les fondements
essentiels de son système philosophique et
scientifique le 10 novembre 1619, pendant la
guerre de trente ans mais dans la solitude
d'une pièce isolée. La partie mathématique
de ses découvertes est évoquée dans le
Discours de la Méthode (1637) et exposée
dans une de ses annexes, la Géométrie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Représenter des solides
Représenter ces solides en perspective cavalière : un cube ; un pavé droit ; un tétraèdre régulier.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Utiliser une translation
Soient \text{ABCD} un parallélogramme et \text{E} un point du plan.

2. Reproduire la figure et construire \text{B}', \text{C}' et \text{D}' les images respectives de \text{B}, \text{C} et \text{D} par t.
3. Quelle est la nature du quadrilatère \text{EB}'\text{C}'\text{D}' ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Utiliser les coordonnées
Le plan est rapporté à un repère (\text{O} \ ; \ \vec{i} \ , \ \vec{j}).On donne les points \text{A}(1\ ; \ 3), \text{B}(-3\ ; \ 1) et \text{C}(0 \ ; \ -2). Déterminer les coordonnées de \text{D} telles que \text{ABCD} soit un parallélogramme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Démontrer à l'aide de vecteurs
Soit \text{ABC} un triangle quelconque. On définit les points \text{R} et \text{S} par \overrightarrow{\mathrm{AR}}=\frac{3}{2} \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{BS}}=\frac{1}{2} \overrightarrow{\mathrm{CB}}. Démontrer que (\mathrm{AC}) / /(\mathrm{SR}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Résoudre un système
Résoudre dans \R ^3 les systèmes d'équations suivants d'inconnue (x \ ; \ y \ ; \ z).
1. \left\{\begin{aligned}
x+y+z &=0 \\
x+y &=0 \\
2 x+y &=0
\end{aligned}\right.
2. \left\{\begin{aligned} x+y+z &=1 \\ 2 x-y &=2 \\ x-y+z &=3 \end{aligned}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Démontrer un alignement
Le plan est rapporté à un repère (\text{O} \ ; \ \vec{i} \ , \ \vec{j}).On donne les points \text{A}(1\ ; \ \dfrac{1}{2}) et \text{B}(-2\ ; \ -1). Les points \text{O}, \text{A} et \text{B} sont-ils alignés ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Problème
Soit \text{ABC} un triangle. On notre \text{I}, \text{J} et \text{K} les milieux respectifs des segments [\text{AB}], [\text{BC}] et [\text{AC}].
On veut démontrer que les trois médianes du triangle \text{ABC} sont concourantes.
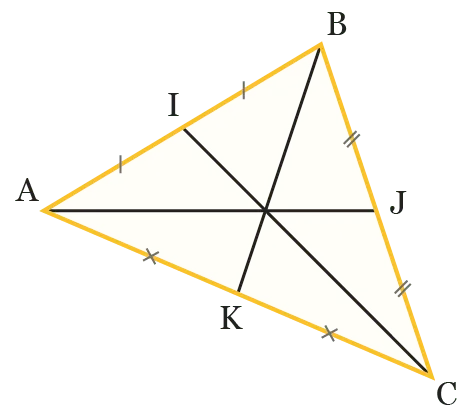
Le plan est rapporté au repère ( \text{A} \ ; \ \overrightarrow{\text{AC}} \ ; \ \overrightarrow{\text{AB}}).
1. Déterminer les coordonnée des points \text{A}, \text{B}, \text{C}, \text{I}, \text{J} et \text{K }dans ce repère.
2. Déterminer une équation de la droite \text{(AJ)}.
2. Déterminer une équation de la droite \text{(AJ)}.
3. Déterminer une équation de la droite \text{(CI)}.
4. Déterminer une équation de la droite \text{(BK)}.
5. Démontrer que les trois droites \text{(AJ)}, \text{(CI)} et \text{(BK)} sont concourantes.
4. Déterminer une équation de la droite \text{(BK)}.
5. Démontrer que les trois droites \text{(AJ)}, \text{(CI)} et \text{(BK)} sont concourantes.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

