Chapitre 9
Cours
Proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Proportionnalité
Définitions
Deux grandeurs sont proportionnelles lorsque l'on peut passer des valeurs de l'une aux valeurs de l'autre en multipliant par un même nombre non nul, appelé coefficient de proportionnalité. Pour les représenter, on utilise un tableau de proportionnalité.
Exemple :
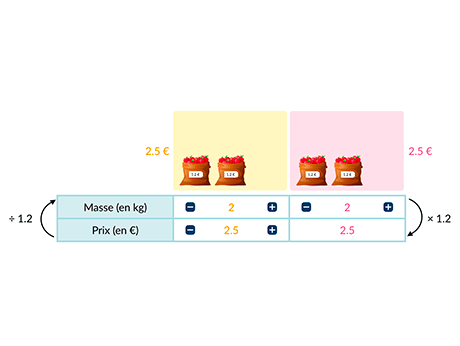
Des pommes sont vendues à 2,50~€/\mathrm{kg} (euro par kg). Le prix payé (en euro) est proportionnel à la masse de pomme achetée (en kilogramme).
2,5 est le coefficient de proportionnalité. On le trouve en calculant le quotient de n'importe quel prix par la masse correspondante.
Des pommes sont vendues à 2,50~€/\mathrm{kg} (euro par kg). Le prix payé (en euro) est proportionnel à la masse de pomme achetée (en kilogramme).
 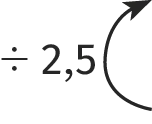 |
Masse (en kg)
|
1
|
2
|
6
|
8,1
|  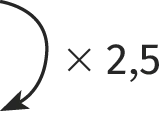 |
|---|---|---|---|---|---|---|
Prix (en €)
|
2,50
|
5
|
15
|
20,25
|
2,5 est le coefficient de proportionnalité. On le trouve en calculant le quotient de n'importe quel prix par la masse correspondante.
Définition
La proportion d'une partie d'un ensemble est définie par le quotient :
\mathrm{Proportion}=\frac{\mathrm{Nombre~d'éléments~de~la~partie}}{\mathrm{Nombre~total~d'éléments}}.
Exemple :
Dans un sac, il y a deux boules blanches et huit boules noires. La proportion de boules blanches dans le sac est donc \frac{2}{10}=0,2=20~\%.
Dans un sac, il y a deux boules blanches et huit boules noires. La proportion de boules blanches dans le sac est donc \frac{2}{10}=0,2=20~\%.
- Remarque : Une proportion est toujours inférieure ou égale à 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Utiliser une échelle
Définition
L'échelle d'un plan est le coefficient de proportionnalité entre les distances représentées sur un plan et les distances réelles, exprimées dans la même unité.
\mathrm{Échelle}=\frac{\mathrm{Distance~sur~le~plan}}{\mathrm{Distance ~réelle}}
Exemple :
6,5~\mathrm{cm} sur la carte correspondent alors à 650~000~\mathrm{cm} dans la réalité, soit 6,5~\mathrm{km}.
6,5~\mathrm{cm} sur la carte correspondent alors à 650~000~\mathrm{cm} dans la réalité, soit 6,5~\mathrm{km}.
 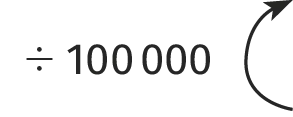 |
Distance sur la carte (en \mathrm{cm})
|
1
|
6,5
|  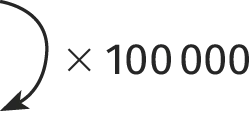 |
|---|---|---|---|---|
Distance dans la réalité (en \mathrm{cm})
|
100~000
|
650~000
|
- Remarque : Une échelle peut se noter de manière graphique en mesurant la longueur du segment donné.
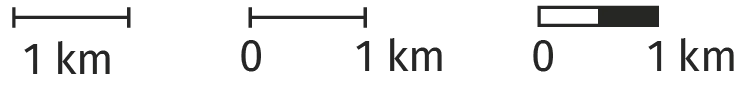
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Résoudre des problèmes
Méthode 1 : Passage à l'unité
Dans un magasin, on vend des crayons à l'unité. Pour trois crayons, on paie 3,60~€. Combien paiera-t-on pour cinq crayons ?
Pour résoudre ce problème, on peut chercher le prix d'un seul crayon : c'est le passage à l'unité.

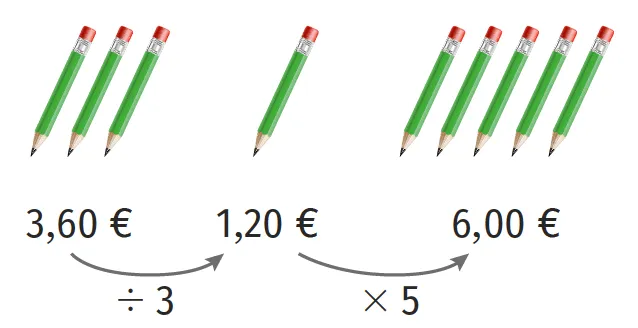
- 3,60 ÷ 3 = 1,20 : un crayon coûte 1,20~€.
- 1,20 × 5 = 6 : cinq crayons coûtent au total 6~€.
Méthode 2 : Appliquer un pourcentage avec un schéma en barres
Dans un village de 800 personnes, 20~\% sont des enfants. Combien y a-t-il d'enfants ?
On partage le schéma en barres en 10. 100~\%÷ 10 = 10~\% donc chaque rectangle représente 10~\%.
800 ÷ 10 = 80 donc chaque rectangle représente aussi 80 personnes.
Ainsi, 10~\% représentent 80 personnes.


On en déduit que 20~\% représentent 160 personnes. Il y a 160 enfants dans ce village.
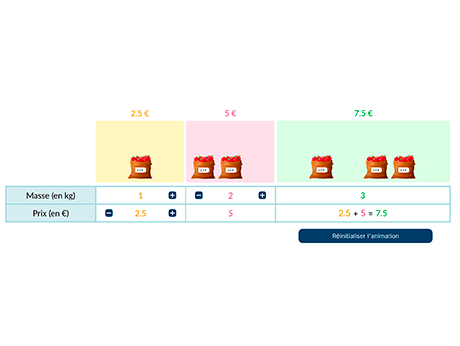
Méthode 3 : Opérations sur les colonnes
Zélie participe à une session de karting. En faisant trois tours de piste, elle parcourt une distance totale de 4,95~\mathrm{km}. Aujourd'hui, elle décide de faire douze tours de piste. Quelle distance va-t-elle parcourir ? Quelle distance parcourrait-elle en quinze tours ?
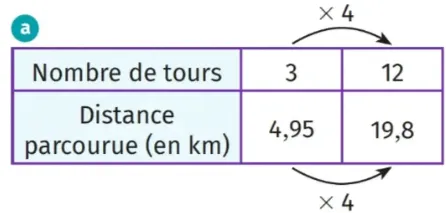
Douze tours : si Zélie fait quatre fois plus de tours, elle parcourra quatre fois plus de distance. 4,95 × 4 = 19,8. Zélie parcourra 19,8~\mathrm{km} en douze tours (tableau (a)).
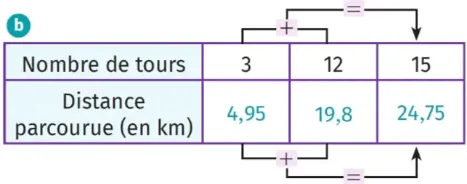
Quinze tours : pour réaliser quinze tours, Zélie fait d'abord douze tours (par exemple) puis trois tours. Ce qui fait donc 19,8~\mathrm{km} suivis de 4,95~\mathrm{km}. 19,8 + 4,95 = 24,75. Zélie parcourra 24,75~\mathrm{km} en quinze tours (tableau (b)).
Dans un tableau de proportionnalité, on peut déterminer les valeurs d'une colonne en :
- multipliant ou divisant les valeurs d'une colonne par un même nombre non nul ;
- ajoutant ou soustrayant les valeurs de deux colonnes.


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille