Chapitre 10
Entrée en matière
Durées
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLa division du temps
Pour mesurer les grandeurs, nous utilisons aujourd'hui un
système d'unité dit « décimal ». Par exemple, pour passer
d'une unité de longueur à une autre, on multiplie par 10 :
1 \mathrm{~m}=10 \mathrm{~dm}=100 \mathrm{~cm}, etc.
La mesure du temps est l'une des seules exceptions. En effet, une heure comprend 60 minutes et chaque minute contient 60 secondes. Pourquoi ? Il s'agit d'un héritage de la Mésopotamie. À partir du IIIe millénaire avant notre ère, le système numérique en base 60 était utilisé : il y avait des symboles jusqu'à 60 qui pouvaient être combinés pour compter au-delà.
60 étant divisible par 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 et 60, cela est très avantageux pour diviser le temps sans avoir de nombre à virgule.
Cette division du temps est restée jusqu'à aujourd'hui, malgré une tentative après la Révolution française de changer pour des journées de 10 heures, chacune de 100 minutes, elles-mêmes comportant 100 secondes.
La mesure du temps est l'une des seules exceptions. En effet, une heure comprend 60 minutes et chaque minute contient 60 secondes. Pourquoi ? Il s'agit d'un héritage de la Mésopotamie. À partir du IIIe millénaire avant notre ère, le système numérique en base 60 était utilisé : il y avait des symboles jusqu'à 60 qui pouvaient être combinés pour compter au-delà.
60 étant divisible par 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 et 60, cela est très avantageux pour diviser le temps sans avoir de nombre à virgule.
Cette division du temps est restée jusqu'à aujourd'hui, malgré une tentative après la Révolution française de changer pour des journées de 10 heures, chacune de 100 minutes, elles-mêmes comportant 100 secondes.
Horloge révolutionnaire.
Comparer le nombre de secondes dans un jour défini par la Révolution française
avec le nombre de secondes dans nos jours actuels.
Supplément numérique
Retrouvez cette histoire en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
La Terre est ronde et tourne sur elle-même.
Par conséquent, à un même instant,
l'ensoleillement n'est pas le même dans
deux zones géographiques distinctes.
Pour organiser la vie quotidienne, de sorte qu'il fasse nuit à minuit et jour à midi, le globe terrestre est divisé en fuseaux horaires. Quand deux villes se trouvent sur le même fuseau horaire, il est la même heure au même instant.
Selon ces fuseaux horaires, quand il est 11\text{ h} à Paris, il est 5\text{ h} à Montréal au Canada.
Pour organiser la vie quotidienne, de sorte qu'il fasse nuit à minuit et jour à midi, le globe terrestre est divisé en fuseaux horaires. Quand deux villes se trouvent sur le même fuseau horaire, il est la même heure au même instant.
Selon ces fuseaux horaires, quand il est 11\text{ h} à Paris, il est 5\text{ h} à Montréal au Canada.
1. Quelle heure est-il à Montréal lorsqu'il est 14\text{ h} à Paris ?
2. Quelle heure est-il à Paris lorsqu'il est 17\text{ h} à Montréal ?
2. Quelle heure est-il à Paris lorsqu'il est 17\text{ h} à Montréal ?
Supplément numérique
Visualisez
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ActivitéComprendre un planning
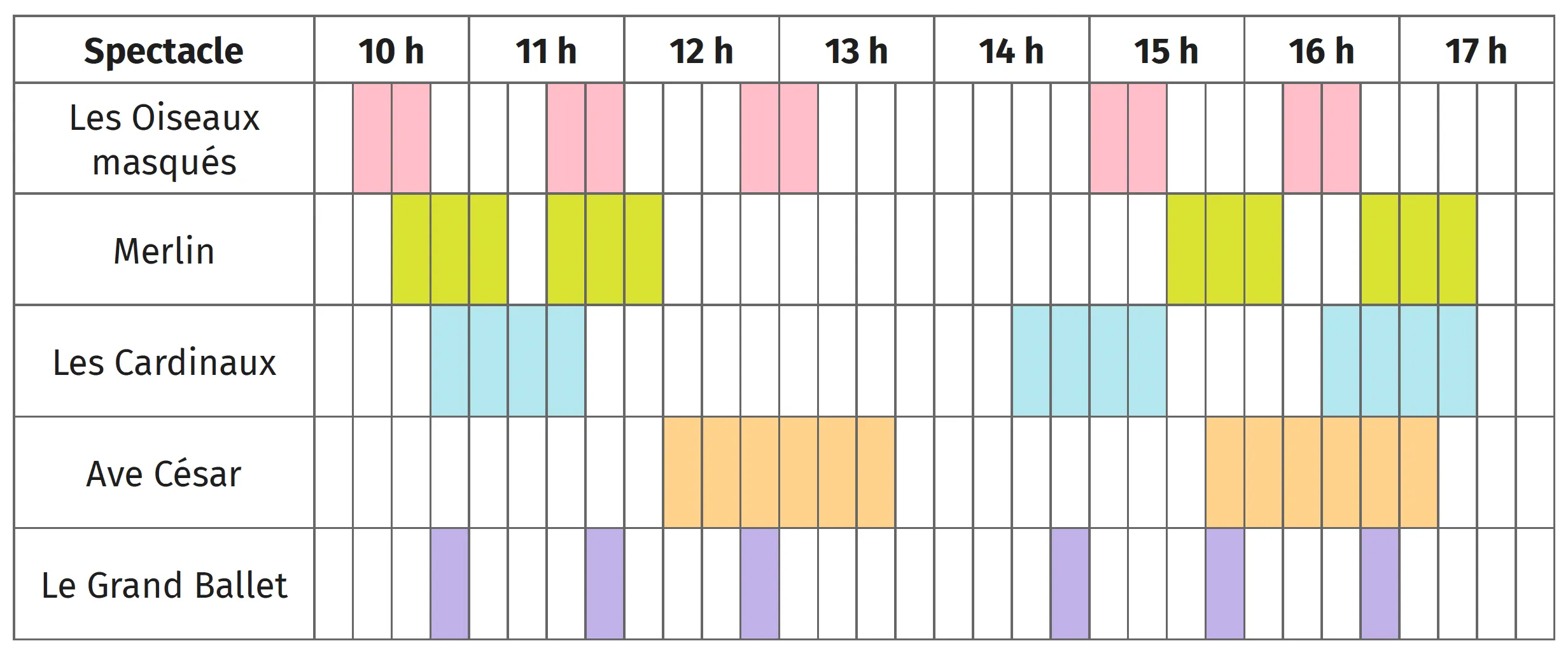
Voici les horaires des spectacles du jour dans un parc à thème. Chaque case correspond à une
plage horaire de 15 minutes ; les cases colorées consécutives correspondent à la durée du
spectacle.
1.
Déterminer la durée en minute de chaque spectacle.
2.
Selon ce tableau, combien de représentations a le spectacle « Les Oiseaux masqués » ?
Indiquer l'horaire de début et de fin de chacune des représentations de ce spectacle.
3.
Sébastien et Karine veulent voir tous les spectacles au cours de la même journée. Établir
un planning afin qu'ils assistent à chaque spectacle une fois, en leur prévoyant au moins
15 minutes de trajet entre deux spectacles.
Expliquer la différence entre un horaire et une durée.
Bilan
Expliquer la différence entre un horaire et une durée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationFabriquer et utiliser une horloge
Pour réaliser cette activité, télécharger cette .
1. Pour chaque question, positionner les aiguilles sur l'heure de départ donnée puis appliquer les durées demandées pour lire l'heure finale obtenue.
a. Il est 9 \text{h} 15. Ajouter 30 \text{min}, puis 15 \text{min}, puis 1 \text{h}, et enfin 8 \text{min}. Quelle heure est-il ?
b. Il est 22 \text{h} 38. Ajouter 40 \text{min}, retirer 5 \text{min}, ajouter 21 \text{min}, retirer 7 \text{min}. Quelle heure est-il ?
c. Il est 13 \text{h} 25. Il s'écoule 72 minutes. Quelle heure est-il ?
1. Pour chaque question, positionner les aiguilles sur l'heure de départ donnée puis appliquer les durées demandées pour lire l'heure finale obtenue.
a. Il est 9 \text{h} 15. Ajouter 30 \text{min}, puis 15 \text{min}, puis 1 \text{h}, et enfin 8 \text{min}. Quelle heure est-il ?
2. Toujours à l'aide de l'horloge, positionner les aiguilles sur l'heure de départ indiquée
et déterminer la durée qui s'est écoulée entre les deux horaires donnés.
a. Heure de départ : 15 \text{h} 03 ; heure d'arrivée : 15 \text{h} 27.
b. Heure de départ : 16 \text{h} 47 ; heure d'arrivée : 17 \text{h} 29.
c. Heure de départ : 11 \text{h} 53 ; heure d'arrivée : 13 \text{h} 28.
Rédiger une méthode pour additionner des durées, notamment lorsque celles-ci dépassent 60 minutes.
Bilan
Rédiger une méthode pour additionner des durées, notamment lorsque celles-ci dépassent 60 minutes.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
