Chapitre 11
Savoir-faire
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
MéthodeCalculer des probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Énoncé
On tire au hasard une des boules ci-contre. Calculer la probabilité :1. d'obtenir une boule verte ;
2. d'obtenir une boule avec un nombre (seul ou avec une lettre) ;
3. d'obtenir une boule qui contient à la fois une lettre et un nombre ;
4. d'obtenir une boule noire.


Solution commentée
Dans chaque cas, on compte le nombre de boules parmi les six qui respectent la
condition donnée.1. Il y a une seule boule verte sur un total de six boules.
La probabilité d'obtenir une boule verte est égale à \frac{1}{6}.
2. Il y a quatre boules avec un nombre sur un total de six boules.
La probabilité d'obtenir une boule avec un nombre est égale à \frac{4}{6}.
3. Il y a deux boules avec à la fois un nombre et une lettre.
La probabilité d'obtenir une boule qui contient à la fois un lettre et un nombre est égale à \frac{2}{6}.
4. Il n'y a pas de boule noire.
C'est un événement impossible. Sa probabilité est égale à 0.
Supplément numérique
La méthode .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À mon tour
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour les exercices 7 à 11, on considère
l'expérience aléatoire suivante : on choisit au
hasard une lettre de l'alphabet français.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Quelle est la probabilité d'obtenir \mathrm{M} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Quelle est la probabilité d'obtenir une
voyelle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Quelle est la probabilité d'obtenir l'une
des dix premières lettres de l'alphabet ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
Quelle est la probabilité d'obtenir \mathrm{3} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
Quelle est la probabilité d'obtenir une
lettre du mot « maman » ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
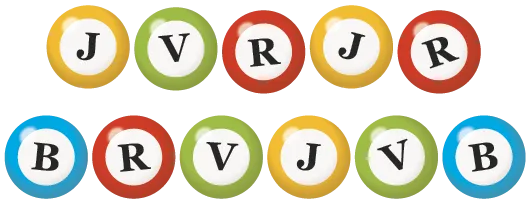
Pour les exercices
12 à 14, on tire au
hasard une des
boules ci-contre.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Générateur d'exercices
Générateur d'exercices
Quelle est la probabilité de tirer une boule jaune ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
Quelle est la probabilité de tirer une
boule verte ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
Quelle est la probabilité de tirer une
boule rouge ou verte ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

