Chapitre 11
Entraînement
Probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Généralités sur les probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15À l'oral
À l'oral
Pour chacune des situations ci-dessous, donner les issues possibles.
1. On lance une pièce de monnaie.
2. On choisit au hasard un jour de la semaine.
3. On choisit au hasard un nombre pair entre 1 et 19.
1. On lance une pièce de monnaie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16À l'oral
À l'oral
Compléter les phrases suivantes.
1. Un événement a 4 chances sur 11 de se réaliser. Sa probabilité est égale à.
2. Un événement a 7 chances sur 7 de se réaliser. Sa probabilité est égale à.
3. Un événement a 99 chances sur 100 de se réaliser. Sa probabilité est égale à.
4. Un événement a 2 chances sur 3 de se réaliser. Sa probabilité est égale à.
1. Un événement a 4 chances sur 11 de se réaliser. Sa probabilité est égale à
2. Un événement a 7 chances sur 7 de se réaliser. Sa probabilité est égale à
3. Un événement a 99 chances sur 100 de se réaliser. Sa probabilité est égale à
4. Un événement a 2 chances sur 3 de se réaliser. Sa probabilité est égale à
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17À l'oral
À l'oral
Pour chacun des nombres suivants,
donner son écriture décimale.
1.
\dfrac{1}{2}
2.
\dfrac{4}{4}
3.
\dfrac{3}{4}
4.
\dfrac{7}{10}
5.
45 \; \%
6.
0 \; \%
7.
12 \; \%
8.
30,4 \; \%
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
1. Parmi les nombres suivants, donner
ceux qui ne peuvent pas représenter une
probabilité.
2. Parmi les nombres restants, quel est celui qui est égal à la probabilité d'un événement très probable ?
2. Parmi les nombres restants, quel est celui qui est égal à la probabilité d'un événement très probable ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
1. Parmi les nombres suivants, donner
ceux qui ne peuvent pas représenter une
probabilité.
2. Parmi les nombres restants, quel est celui
qui est égal à la probabilité de l'événement
certain ? De l'événement impossible ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
On lance un dé équilibré à
huit faces numérotées de 1 à 8.
On s'intéresse au résultat du
lancer.


- \mathrm{A} : « Obtenir le nombre 5. »
- \mathrm{B} : « Obtenir un nombre pair. »
- \mathrm{C} : « Obtenir un multiple de 3. »
- \mathrm{D} : « Obtenir un nombre strictement inférieur à 4. »
- \mathrm{E} : « Obtenir un nombre supérieur à 10. »
- \mathrm{F} : « Obtenir un nombre à la fois multiple de
2 et de 3. »
- \mathrm{G} : « Obtenir un nombre impair multiple de 4. »
- \mathrm{H} : « Obtenir un nombre multiple de 4
supérieur à 6. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
1. Le segment ci-dessous mesure 8 \text{ cm} et représente une échelle de probabilité.
2. Placer approximativement les lettres correspondant aux événements suivants sur le segment à la position appropriée par rapport à leur probabilité.
\mathrm{A} : « Lancer une pièce équilibrée et obtenir
FACE. »
\mathrm{B} : « Piocher une boule bleue dans un sac contenant trois boules bleues et une boule rouge. »
\mathrm{C} : « Lancer un dé équilibré à six faces et obtenir le nombre 2. »
\mathrm{D} : « Choisir au hasard une lettre de l'alphabet et obtenir une voyelle ou une consonne. »
\mathrm{E} : « Gagner au loto trois semaines consécutives. »
2. Placer approximativement les lettres correspondant aux événements suivants sur le segment à la position appropriée par rapport à leur probabilité.
\mathrm{B} : « Piocher une boule bleue dans un sac contenant trois boules bleues et une boule rouge. »
\mathrm{C} : « Lancer un dé équilibré à six faces et obtenir le nombre 2. »
\mathrm{D} : « Choisir au hasard une lettre de l'alphabet et obtenir une voyelle ou une consonne. »
\mathrm{E} : « Gagner au loto trois semaines consécutives. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer des probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
À l'oral
À l'oral
Dans une classe de sixième, il y a douze filles et treize garçons. On choisit
au hasard un élève dans cette classe.
Quelle est la probabilité de choisir un
garçon ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23À l'oral
À l'oral
On choisit au hasard un élève de la classe. Quelle est la probabilité qu'il ait dix-neuf ans ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
On lance un dé non truqué à vingt
faces numérotées de 1 à 20. Quelle est la
probabilité d'obtenir un nombre pair ?
Donner le résultat sous la forme d'une
fraction, puis d'un nombre décimal et d'un
pourcentage.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
On lance un dé non truqué à six faces
numérotées de 1 à 6.
1. Quelle est la probabilité d'obtenir 4 ?
2. Quelle est la probabilité d'obtenir 8 ?
3. Quelle est la probabilité d'obtenir un nombre impair ?
1. Quelle est la probabilité d'obtenir 4 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
On choisit au
hasard une boule
parmi celles-ci.

 1. Quelle est la probabilité d'obtenir une
boule avec le nombre 4 ?
2. Quelle est la probabilité d'obtenir une
boule avec un nombre pair ?
3. Donner un événement certain et un
événement impossible.
1. Quelle est la probabilité d'obtenir une
boule avec le nombre 4 ?
2. Quelle est la probabilité d'obtenir une
boule avec un nombre pair ?
3. Donner un événement certain et un
événement impossible.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Dans un sac, on dispose des jetons
suivants.


On tire un jeton de ce sac au hasard et on s'intéresse au caractère obtenu.
1. Calculer la probabilité d'obtenir la lettre \mathrm{A}.
2. Calculer la probabilité d'obtenir le chiffre 9.
3. Calculer la probabilité d'avoir une voyelle.
4. La probabilité d'obtenir une lettre est-elle
égale à la probabilité d'obtenir un chiffre ?


On tire un jeton de ce sac au hasard et on s'intéresse au caractère obtenu.
1. Calculer la probabilité d'obtenir la lettre \mathrm{A}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
On tire au hasard une pelote de laine
parmi celles ci-dessous.

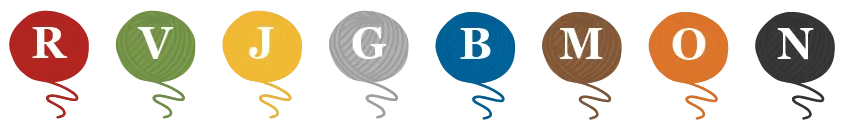 1.
Quelle est la probabilité d'obtenir la
pelote jaune ?
2.
Donner un événement de probabilité \frac{1}{4}.
1.
Quelle est la probabilité d'obtenir la
pelote jaune ?
2.
Donner un événement de probabilité \frac{1}{4}.

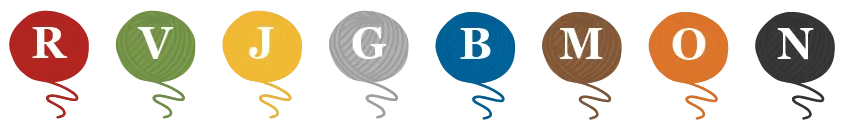
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Copie d'élève
Copie d'élève
On écrit les lettres du mot \mathrm{CALCUL} sur
un dé à six faces et on souhaite calculer la
probabilité d'obtenir la lettre \mathrm{C}.
Donner la bonne réponse à ce problème et
expliquer les erreurs faites par les élèves
ci-dessous.
Copie de Camélia :
Copie de Morgan :
Copie de Camélia :
On peut obtenir les lettres \mathrm{C}, \mathrm{A}, \mathrm{L} et
\mathrm{U} donc on a une chance sur quatre
d'obtenir le \mathrm{C}. La probabilité d'obtenir \mathrm{C}
est égale à \frac{1}{4}.
Copie de Morgan :
Il y a 2 fois la lettre \mathrm{C} et 4 lettres qui ne
sont pas un \mathrm{C}. La probabilité est donc \frac{2}{4}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

