Mathématiques 6e - 2025
Mes Pages
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Aires et volumes
Outils numériques
Résolution de problèmes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Modélisation en barres
Le schéma en barres permet de modéliser un problème en illustrant les différentes relations entre les données de l'énoncé.
Exemple 1 : Modèle additif
Pedro a dépensé 50~€ pour s'acheter un pantalon à 30~€ et une chemise.
Combien coûte la chemise ?
Combien coûte la chemise ?
Même pour un problème simple comme celui-ci, on peut
modéliser la situation à l'aide de barres. La longueur
des barres n'est pas nécessairement proportionnelle à
la valeur qu'elle représente mais il peut être utile de les
faire de longueurs différentes si elles représentent des valeurs différentes.
Finalement, on voit à l'aide des barres que le prix de la chemise est le complément qu'il faut ajouter à 30~€ pour obtenir 50~€. La chemise coûte 50~€-30~€ soit 20~€.
Finalement, on voit à l'aide des barres que le prix de la chemise est le complément qu'il faut ajouter à 30~€ pour obtenir 50~€. La chemise coûte 50~€-30~€ soit 20~€.
Exemple 2 : Modèle multiplicatif
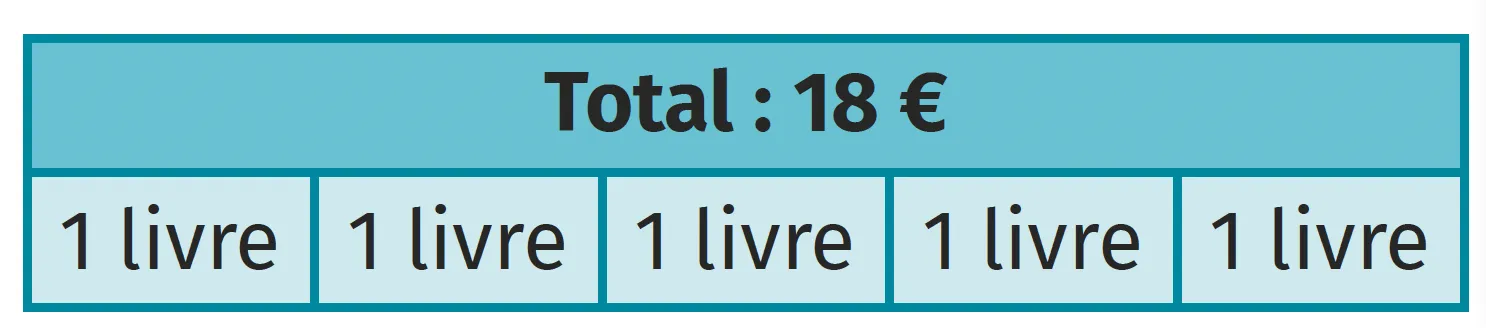
Djema vient d'acheter cinq livres identiques pour un coût total de 18~€.
Combien coûte chaque livre ?
Combien coûte chaque livre ?
Ce problème est de type multiplicatif car on doit
multiplier le prix d'un livre par 5 pour obtenir 18~€.
Ainsi, chaque livre coûte 18~€ ÷ 5 soit 3,60~€.
C'est un exemple de résolution de problème mettant en oeuvre de la proportionnalité.
C'est un exemple de résolution de problème mettant en oeuvre de la proportionnalité.
Exemple 3 : Avec des fractions
Pour aller jouer avec mes amis, j'ai pris toutes mes billes. Durant
la partie, j'en ai perdu les trois septièmes et maintenant, il m'en
reste 20.
Combien avais-je de billes au départ ?
Combien avais-je de billes au départ ?
Les billes perdues représentent
trois septièmes de ce que j'avais au
départ. Je peux donc diviser le total
des billes en sept parts identiques.
On constate que les 20 billes qui restent correspondent à quatre parts. 20 \div 4=5. Chaque part représente donc cinq billes.
J'ai perdu trois parts, ce qui représente 15 billes (3 \times 5).
15+20=35. Au total, j'avais donc 35 billes.
On constate que les 20 billes qui restent correspondent à quatre parts. 20 \div 4=5. Chaque part représente donc cinq billes.
J'ai perdu trois parts, ce qui représente 15 billes (3 \times 5).
15+20=35. Au total, j'avais donc 35 billes.
Exemple 4 : Une situation plus complexe
Pour réaliser un schéma en barres, on peut décider d'une barre unité : par exemple, le montant reçu par l'enfant le plus jeune sera le montant unité. Voilà ce qu'on obtient.
À partir de là, on peut imaginer une nouvelle modélisation car on constate que le total de 75~€ est obtenu en prenant trois fois le montant unité du benjamin ajouté à trois fois 10~€.
Par conséquent, trois unités ensemble valent
15+25+35=75. Le total est bien égal à 75~€.
Une mère distribue 75~€ à ses trois enfants en
fonction de leur âge : l'aîné aura 10~€ de plus que le
cadet et le benjamin aura 10~€ de moins que le cadet.
Combien donne-t-elle à chacun de ses enfants ?
Combien donne-t-elle à chacun de ses enfants ?
Pour réaliser un schéma en barres, on peut décider d'une barre unité : par exemple, le montant reçu par l'enfant le plus jeune sera le montant unité. Voilà ce qu'on obtient.
À partir de là, on peut imaginer une nouvelle modélisation car on constate que le total de 75~€ est obtenu en prenant trois fois le montant unité du benjamin ajouté à trois fois 10~€.
Par conséquent, trois unités ensemble valent
75~€-30~€ = 45~€
et ainsi une unité vaut
45~€ \div 3 soit 15~€. Le benjamin aura 15~€, le cadet 25~€ et l'aîné 35~€.15+25+35=75. Le total est bien égal à 75~€.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'entraîner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Résoudre les exercices suivants en utilisant des schémas en barres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Anna a joué trois matchs au volley cette semaine. Elle a marqué 12 points lors du premier et 17 lors du deuxième.
Sachant qu'elle a marqué 48 points au total, calculer son nombre de points marqués lors du dernier match.
Sachant qu'elle a marqué 48 points au total, calculer son nombre de points marqués lors du dernier match.
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Kaytline a organisé son temps de
travail pour réviser son prochain contrôle
de maths. Elle décide d'apprendre son
cours pendant les quatre neuvièmes du
temps imparti et elle prend les 30 minutes
restantes pour refaire des exercices.
Pendant combien de temps va-t-elle réviser son contrôle ?
Pendant combien de temps va-t-elle réviser son contrôle ?
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Dans une compétition sportive, une
récompense totale de 470~€ est distribuée
aux trois premiers. Le premier gagne 50~€
de plus que le deuxième et le troisième
gagne 30~€ de moins que le deuxième.
Quelle est la somme d'argent attribuée à chaque place ?
Quelle est la somme d'argent attribuée à chaque place ?
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
On observe un bloc de glace de
2~\mathrm{kg} en train de fondre. Lors des deux
premières minutes, il perd \frac{3}{7}~\mathrm{kg}. Les deux
minutes suivantes, il perd \frac{5}{7}~\mathrm{kg}.
Quelle masse exacte reste-t-il ?
Quelle masse exacte reste-t-il ?
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez des
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
