Chapitre 13
Cours
Angles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Angles particuliers
Définitions
Deux demi-droites de même origine peuvent former :
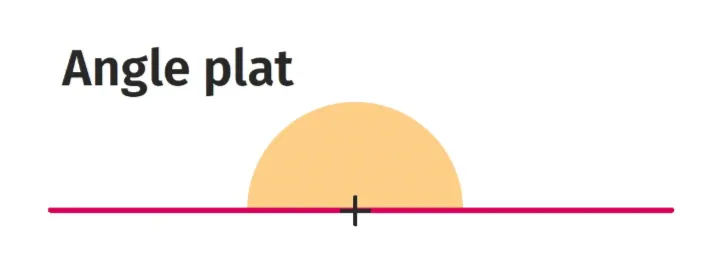
- une droite : l'angle en leur origine est alors appelé angle plat ;
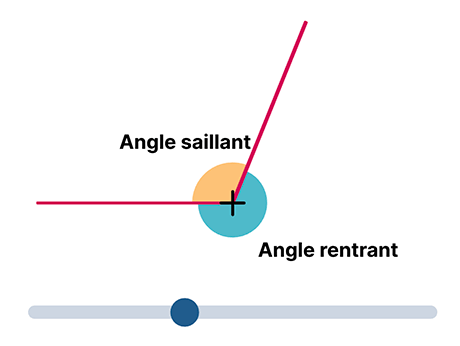
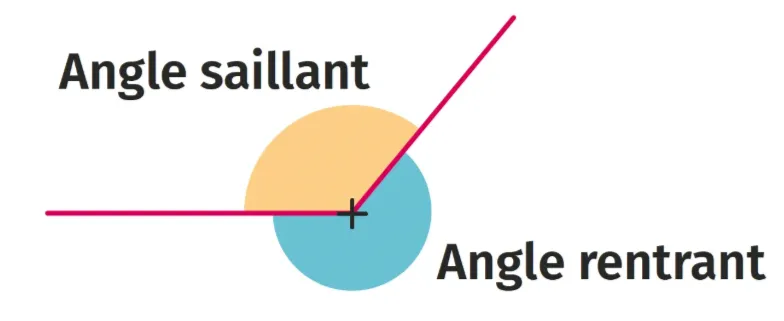
- un angle plus petit que l'angle plat, appelé angle saillant, et un angle plus grand que l'angle plat, appelé angle rentrant ;
- une seule demi-droite si elles sont confondues : l'angle formé à l'origine est, d'une part, l'angle nul, et d'autre part l'angle plein.



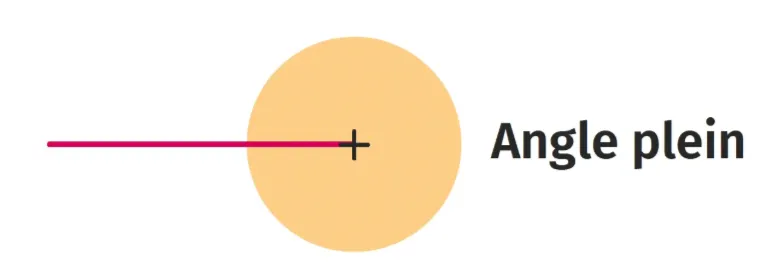
Version interactive
Définition
Lorsque deux droites sécantes se coupent en formant quatre angles égaux, alors chacun des angles obtenus est un angle droit.

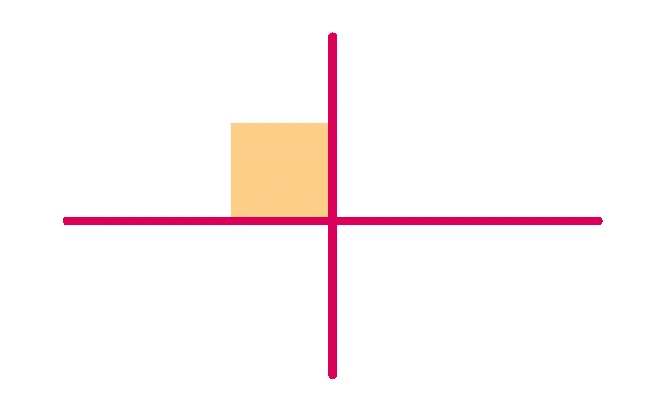
Définitions
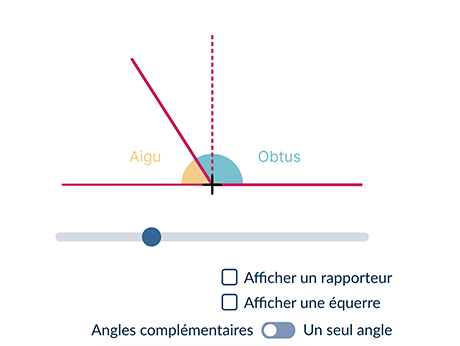
- Un angle aigu est un angle plus petit que l'angle droit.
- Un angle obtus est un angle saillant plus grand que l'angle droit.

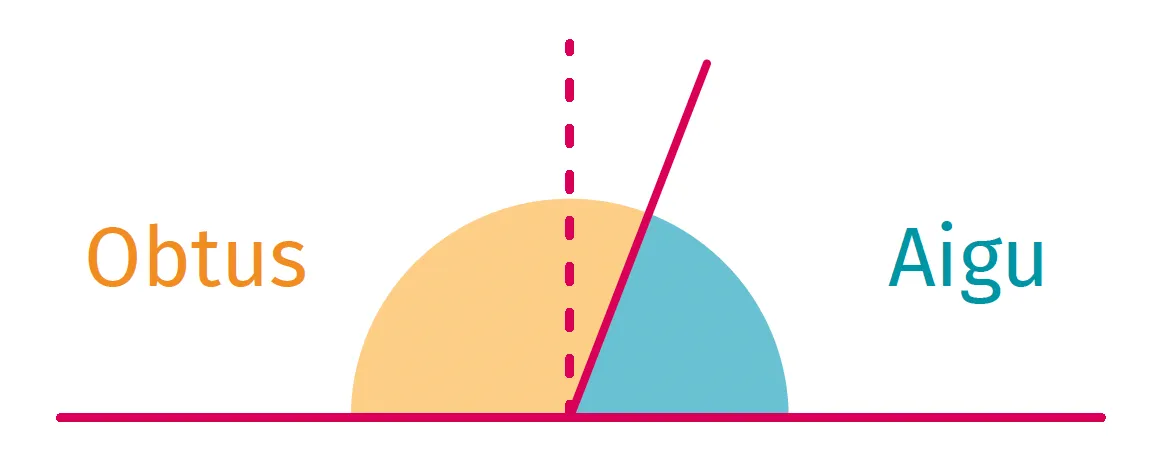
Version interactive
Exemple :
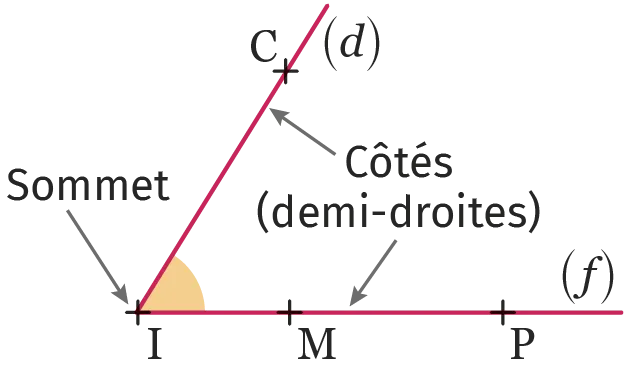
L'angle en orange ci-contre peut être désigné
par \widehat{\text {CIM}}, mais aussi \widehat{\text {MIC}}, \widehat{\text {CIP}} ou même \widehat{d\text {I}f}.
Lorsqu'il n'y a pas d'ambiguïté possible,
on peut simplement écrire \widehat{\text {I}}.

Version interactive
Définitions
Deux angles sont dits :
- supplémentaires lorsqu'ils forment à eux deux un angle plat ;
- adjacents lorsqu'ils ont le même sommet et un côté commun ; opposés par le sommet lorsqu'ils ont le même sommet et les côtés de l'un sont le prolongement de ceux de l'autre.
Exemple : \widehat{\text {AOB}} et \widehat{\text {BOC}} sont adjacents et supplémentaires.
\widehat{\text {AOB}} et \widehat{\text {DOC}} sont des angles opposés par le sommet.
\widehat{\text {AOB}} et \widehat{\text {DOC}} sont des angles opposés par le sommet.


• Remarque : Deux angles supplémentaires ne sont pas forcément adjacents.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Mesure en degré d'un angle
Définition
Le degré d'angle, noté « ^{\circ} », est une des unités de mesure d'un angle. Il correspond au partage d'un angle plat en 180 angles égaux mesurant chacun 1^{\circ}.
Propriété
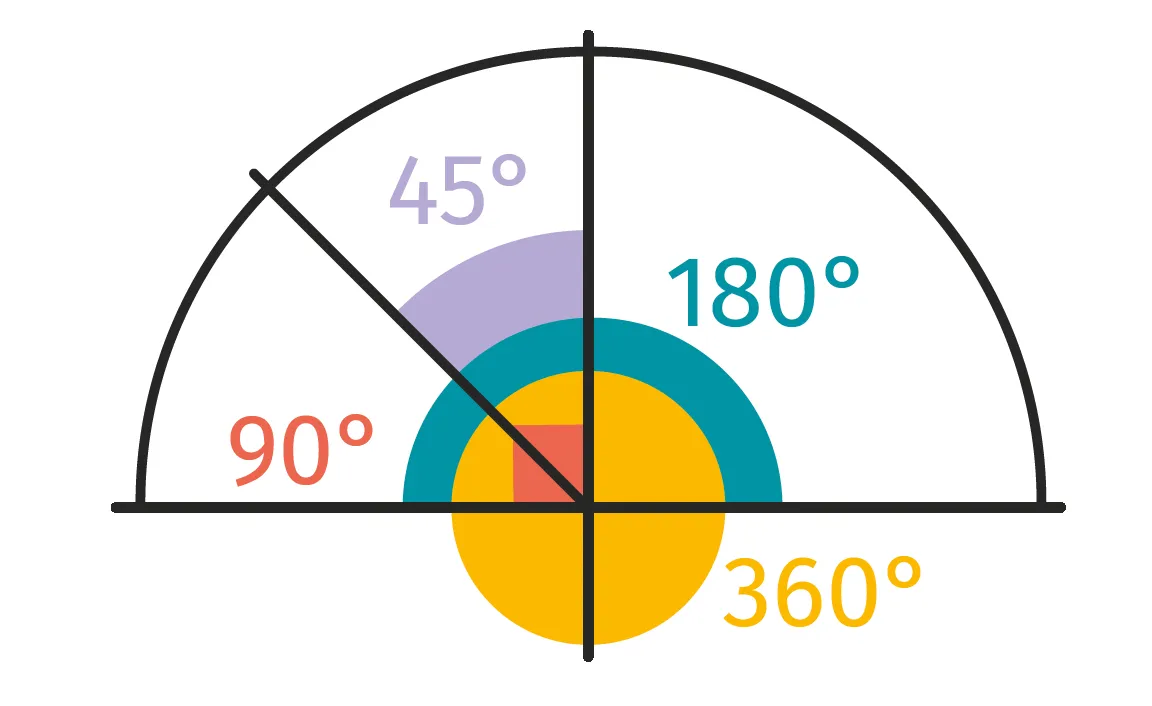
- Un angle plein correspond à un tour complet. Il mesure 360^{\circ}.
- Un angle plat correspond à un demi-tour. Il mesure 180^{\circ}.
- Un angle droit correspond à un quart de tour. Il mesure 90^{\circ}.
- Un angle nul mesure 0^{\circ}.

• Remarque : La somme des mesures d'angles supplémentaires est donc égale à 180^{\circ}.
Exemple :
On fait tourner une roue d'un quart de tour dans un sens, puis d'un demi-tour dans le même sens. On a donc fait tourner la roue de 90^{\circ} puis de 180^{\circ}, soit un total de 270^{\circ}.
On fait tourner une roue d'un quart de tour dans un sens, puis d'un demi-tour dans le même sens. On a donc fait tourner la roue de 90^{\circ} puis de 180^{\circ}, soit un total de 270^{\circ}.
Propriété
Deux angles opposés par le sommet ont la même mesure.
Définition
La bissectrice d'un angle est la demi-droite qui partage cet angle en deux angles adjacents égaux.
Exemple :
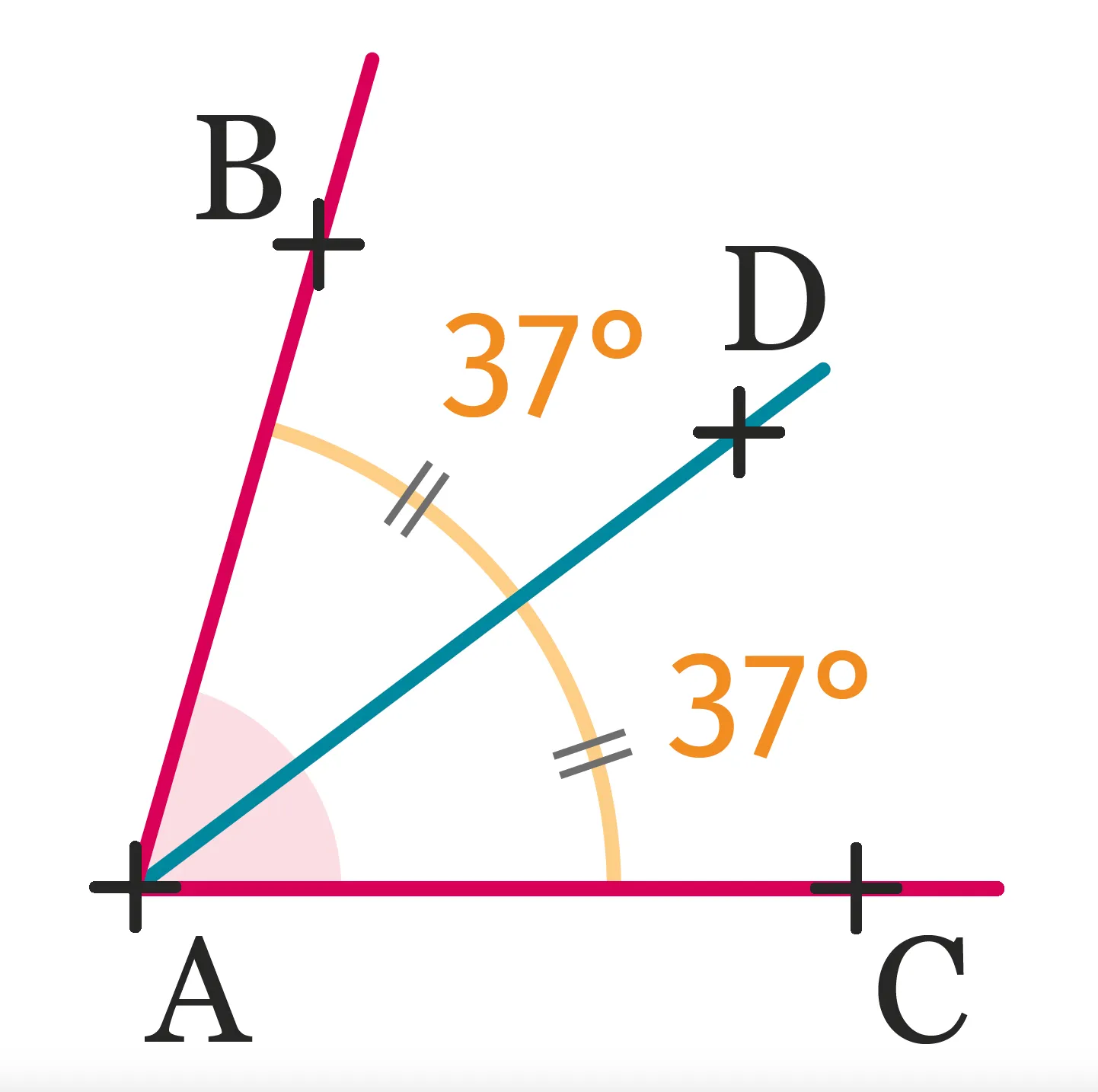
La demi-droite \mathrm{[AD)} est la bissectrice de l'angle \widehat{\mathrm{BAC}} puisque :
1. \widehat{\mathrm{BAD}} et \widehat{\mathrm{DAC}} sont adjacents.
2. \widehat{\mathrm{BAD}}=\widehat{\mathrm{DAC}}=37^{\circ}.
La demi-droite \mathrm{[AD)} est la bissectrice de l'angle \widehat{\mathrm{BAC}} puisque :
1. \widehat{\mathrm{BAD}} et \widehat{\mathrm{DAC}} sont adjacents.
2. \widehat{\mathrm{BAD}}=\widehat{\mathrm{DAC}}=37^{\circ}.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille