Chapitre 16
Entraînement
Symétrie axiale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Médiatrice
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18À l'oral
À l'oral
Pour chaque affirmation, dire si elle
est vraie ou fausse. Justifier.
1. La médiatrice d'un segment passe par le milieu de ce segment.
2. Si \mathrm{EF}=\mathrm{EG}, alors \text {E} est le milieu
de \text {[FG]}.
3. Si une droite passe par le milieu d'un
segment, alors elle est la médiatrice de
ce segment.
1. La médiatrice d'un segment passe par le milieu de ce segment.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19À l'oral
À l'oral
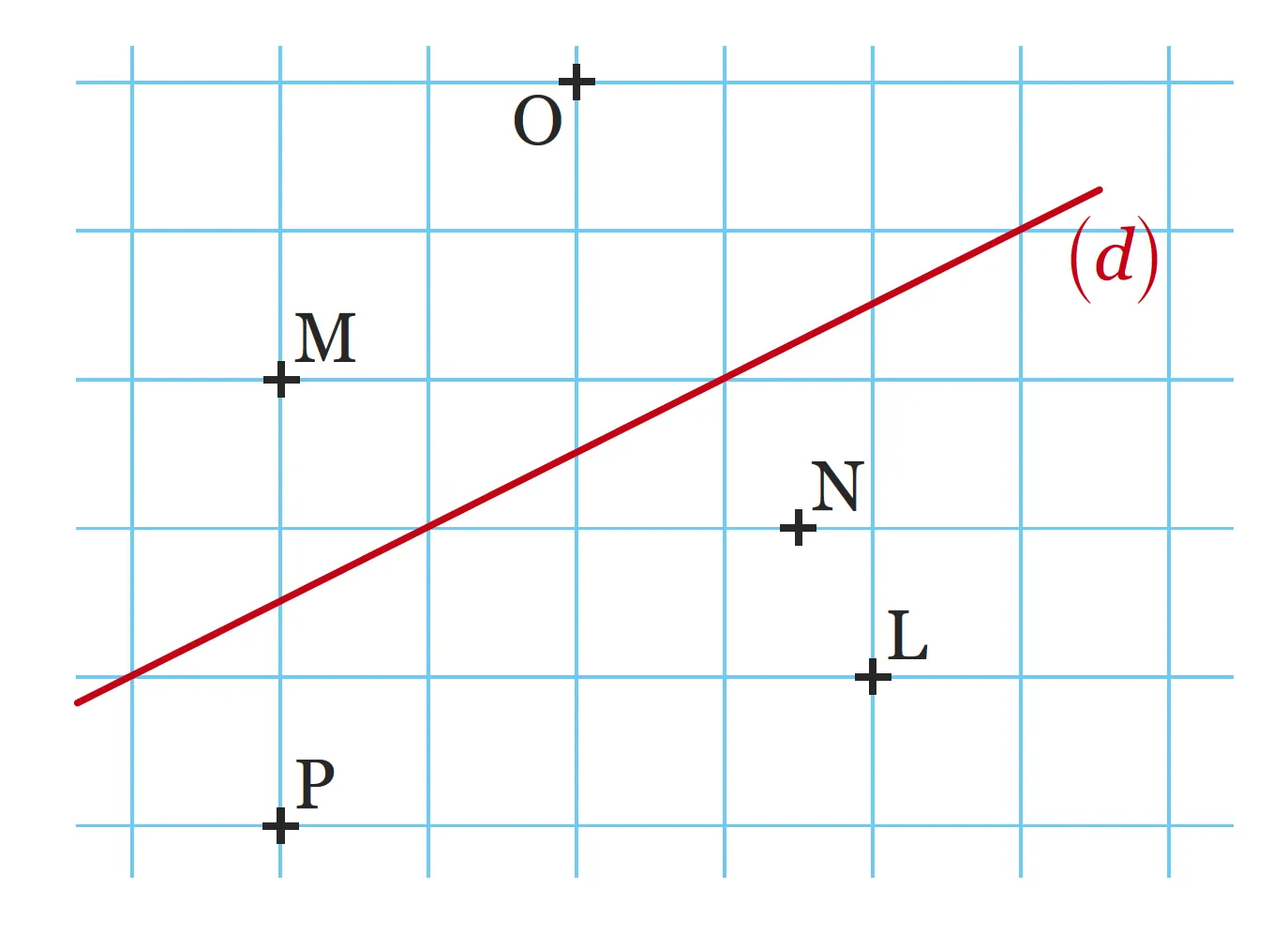
De quel segment la droite (d) est-elle la médiatrice ? Justifier en utilisant
le quadrillage.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20À l'oral
À l'oral
Expliquer comment tracer la médiatrice d'un segment à l'aide d'une règle graduée et d'une équerre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21À l'oral
À l'oral
Expliquer comment tracer la
médiatrice d'un segment en utilisant la
règle et le compas.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
On considère trois points \text {K}, \text {L} et \text {M} alignés dans cet ordre.
Où doit-on placer le point \text {L} pour qu'il appartienne à la médiatrice de \text {[KM]} ?
Où doit-on placer le point \text {L} pour qu'il appartienne à la médiatrice de \text {[KM]} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Générateur d'exercices
Générateur d'exercices
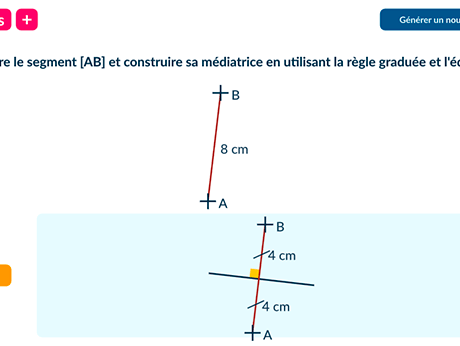
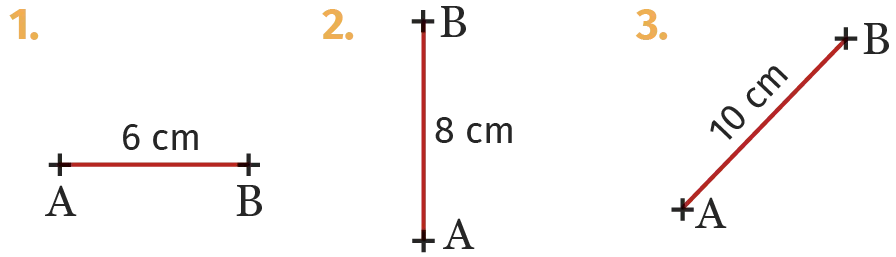
Dans chaque cas, reproduire le segment
\text {[AB]} et construire sa médiatrice en utilisant
la règle graduée et l'équerre.



Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
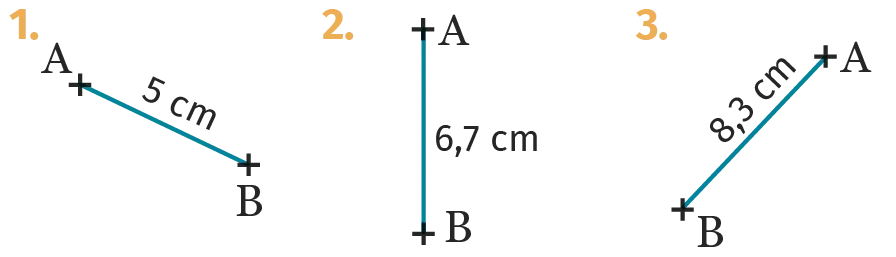
Dans chaque cas, reproduire le segment
\text {[AB]} et construire sa médiatrice en utilisant
la règle et le compas.



Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Tracer un segment \text {[MN]} sur un petit
morceau de papier blanc, puis construire sa
médiatrice par pliage, sans équerre ni compas.
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Tracer un segment \text {[CD]} de longueur
7 \mathrm{~cm}. Construire exactement trois points
équidistants de \text {C} et de \text {D}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Placer deux points \text {S} et \text {T} distincts.
Construire l'ensemble des points
équidistants de \text {S} et de \text {T}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
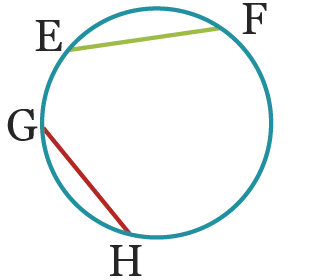
Reproduire
approximativement la
figure suivante dans
laquelle le cercle a un
rayon de 4,2 \mathrm{~cm}.

Cliquez pour accéder à GeoGebra


1. Tracer les médiatrices des cordes \text {[EF]} et \text {[GH]}. On note \text{A} leur point d'intersection.
2. Que dire du point \text {A} par rapport au cercle ?
3. Le point \text{A} appartient-il à la médiatrice de \text {[EG]} ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
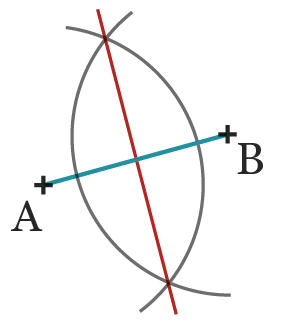
Quelle propriété de la médiatrice permet de justifier sa construction à l'aide d'un compas et d'une règle non graduée.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
Réaliser le programme de construction
suivant.
1. Tracer un cercle de centre \text {K} et de rayon 4,1~\mathrm{cm}.
2. Tracer une corde \text {[GH]}.
3. Construire la médiatrice de \text {[GH]}.
4. Placer un point \text {M} sur le cercle, tel que \text {M} soit équidistant de \text {G} et de \text {H}.
1. Tracer un cercle de centre \text {K} et de rayon 4,1~\mathrm{cm}.
2. Tracer une corde \text {[GH]}.
3. Construire la médiatrice de \text {[GH]}.
4. Placer un point \text {M} sur le cercle, tel que \text {M} soit équidistant de \text {G} et de \text {H}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
Remettre dans l'ordre la définition
suivante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
Remettre dans l'ordre la propriété suivante.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
À l'aide de l'équerre, identifier
les prénoms des personnes qui sont
respectivement :

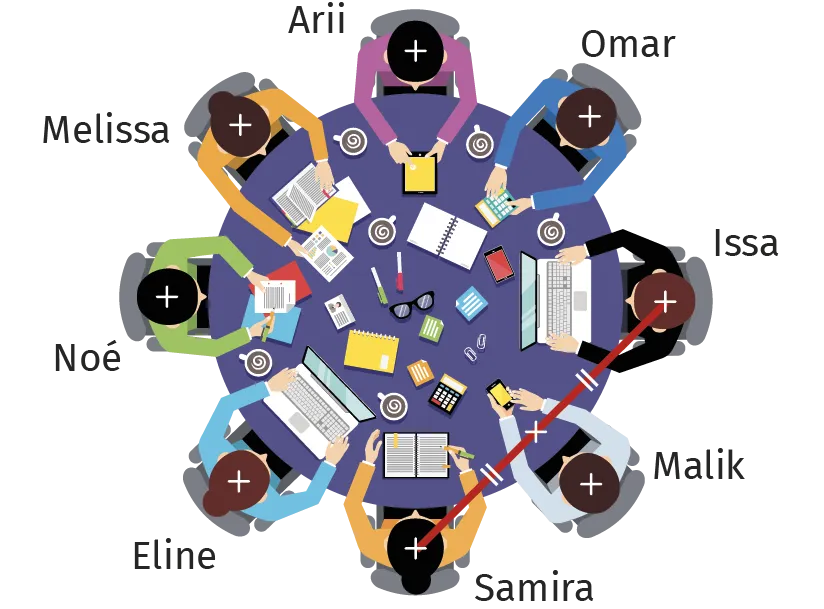


1. équidistantes d'Issa et de Samira ;
2 situées plus près d'Issa que de Samira ;
3. situées plus près de Samira que d'Issa.
2 situées plus près d'Issa que de Samira ;
3. situées plus près de Samira que d'Issa.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
La est à télécharger.

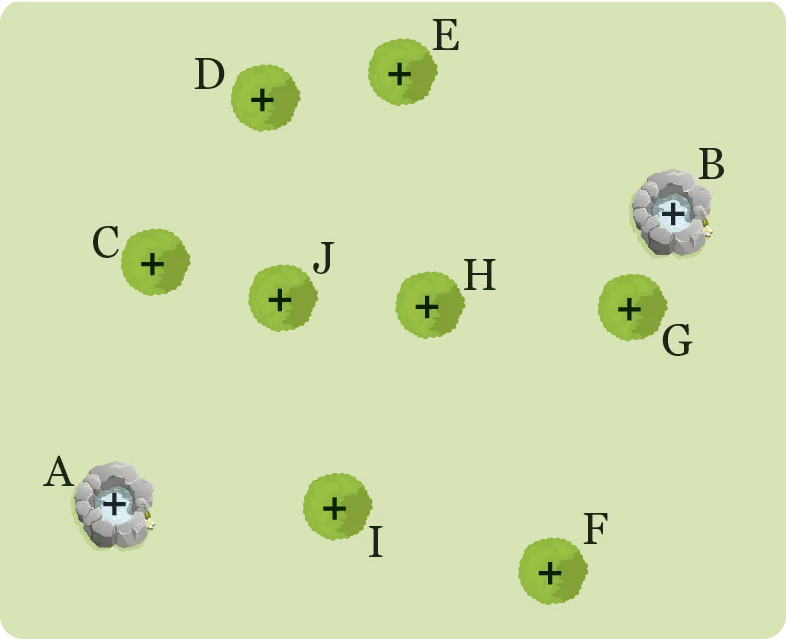
Dans le jardin schématisé ici, il y
a deux points d'eau notées \text {A} et \text {B}. Pour
arroser un arbre, il est préférable d'utiliser
le point d'eau le plus proche. Quel point
d'eau est-il préférable d'utiliser pour arroser
chacun des arbres ? Justifier.


Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Exercice inversé
Exercice inversé
Écrire l'énoncé d'un exercice
dont la réponse serait : « La droite
\text {(AM)} est la médiatrice du segment
\text {[BC]}. »
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Copie d'élève
Copie d'élève
Une professeure demande à ses
élèves de tracer un segment \text {[EF]} et
d'expliquer les étapes pour construire sa
médiatrice. Voici la réponse d'un élève.
Quelle erreur a-t-il commise ? Corriger sa copie.
Je place \text {G} le milieu de \text {[EF]} et je trace une
droite passant par \text {G}.

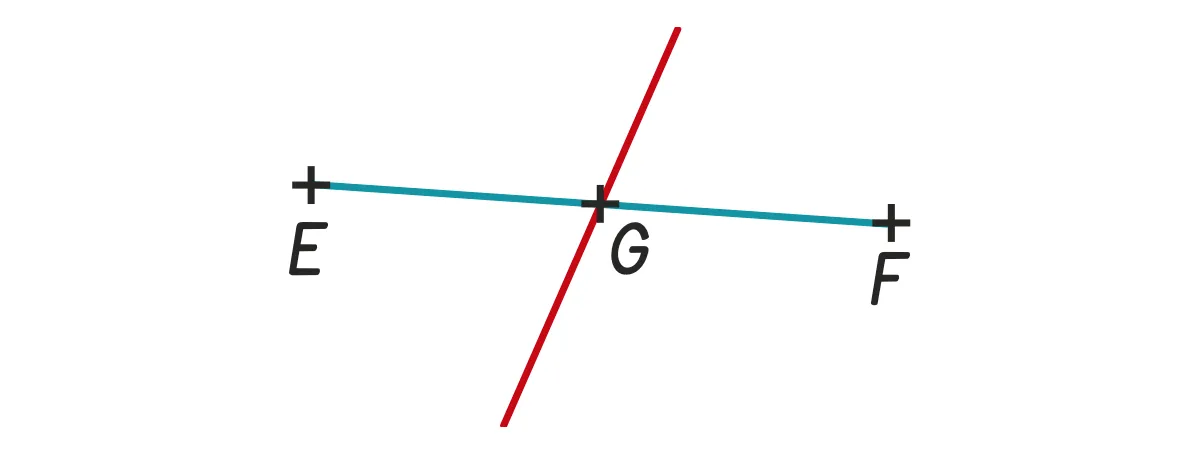


Quelle erreur a-t-il commise ? Corriger sa copie.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
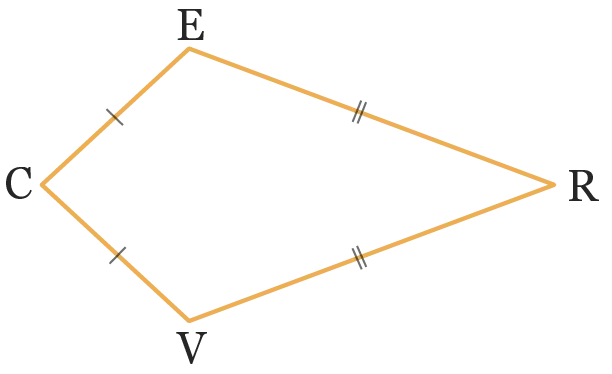
Sur la figure ci-dessous, est-ce la droite
(\mathrm{EV}) qui est la médiatrice du segment \text {[CR]}
ou bien la droite (\mathrm{CR}) qui est la médiatrice
du segment \text {[EV]} ? Justifier.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Réaliser le programme de construction
suivant.
- Placer deux points \text {S} et \text {T} distincts.
- À la règle et au compas, construire la médiatrice du segment \text {[ST]}.
- Colorier d'une couleur la région contenant les points plus proches de \text {S} que de \text {T} et d'une autre couleur celle contenant les points plus proches de \text {T} que de \text {S}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
1. Réaliser le programme de
construction suivant.
2. Sans utiliser de mesure et en employant uniquement l'équerre, déterminer précisément le milieu de la corde [\mathrm{BC}]. Justifier.
- Placer deux points \text {A} et \text {B} distincts.
- Tracer le cercle de centre \text {A} et passant par \text {B}.
- Placer un point \text {C} distinct de \text {B} sur ce cercle.
Cliquez pour accéder à GeoGebra
2. Sans utiliser de mesure et en employant uniquement l'équerre, déterminer précisément le milieu de la corde [\mathrm{BC}]. Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
Proposer une méthode pour déterminer
la boule la plus proche du cochonnet
dans une partie de pétanque sans utiliser
d'instrument de mesure.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Un cercle a été tracé et son centre a été effacé. Proposer une méthode pour retrouver le centre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
Un professeur propose des défis
mathématiques dans la cour de récréation.
Pour chaque défi, réaliser un schéma de la position des élèves vue de dessus.
Pour chaque défi, réaliser un schéma de la position des élèves vue de dessus.
- Défi 1 : Tao et Mia sont à trois pas l'un
de l'autre. Sept élèves se placent à égale
distance de ces deux élèves.Cliquez ici pour avoir accès à un espace de dessin
- Défi 2 : Parmi douze élèves, \frac{1}{3} sont
équidistants d'Ivan et de Diana, \frac{1}{3} sont
plus proches d'Ivan et \frac{1}{3} sont plus proches
de Diana.Cliquez ici pour avoir accès à un espace de dessin
- Défi 3 : Huit élèves se placent à quatre pas
de Léonide.Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
Cet exercice est à réaliser en binôme.
1. Placer deux points \text {A} et \text {B} espacés d'environ 10 \mathrm{~cm}.
2. À tour de rôle, en utilisant une couleur différente pour chaque joueur, chacun place cinq points, en cherchant à les positionner à égale distance des points \text {A} et \text {B}. Il est interdit d'utiliser le matériel de géométrie.
3. Tracer ensuite la médiatrice de \text {[AB]}.
4. Le joueur ayant placé le plus de points sur la médiatrice gagne.
1. Placer deux points \text {A} et \text {B} espacés d'environ 10 \mathrm{~cm}.
2. À tour de rôle, en utilisant une couleur différente pour chaque joueur, chacun place cinq points, en cherchant à les positionner à égale distance des points \text {A} et \text {B}. Il est interdit d'utiliser le matériel de géométrie.
3. Tracer ensuite la médiatrice de \text {[AB]}.
4. Le joueur ayant placé le plus de points sur la médiatrice gagne.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
Une professeure d'EPS organise un jeu
pour ses élèves. Deux d'entre eux se tiennent
à une distance de dix pas l'un de l'autre.
Le défi consiste à placer un plot de manière
à ce que les deux joueurs aient les mêmes
chances de l'atteindre en premier.
Déterminer plusieurs positions où placer le plot pour que le jeu soit équitable.
Réaliser un schéma pour illustrer la solution.
Déterminer plusieurs positions où placer le plot pour que le jeu soit équitable.
Réaliser un schéma pour illustrer la solution.
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Symétrie axiale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45À l'oral
À l'oral
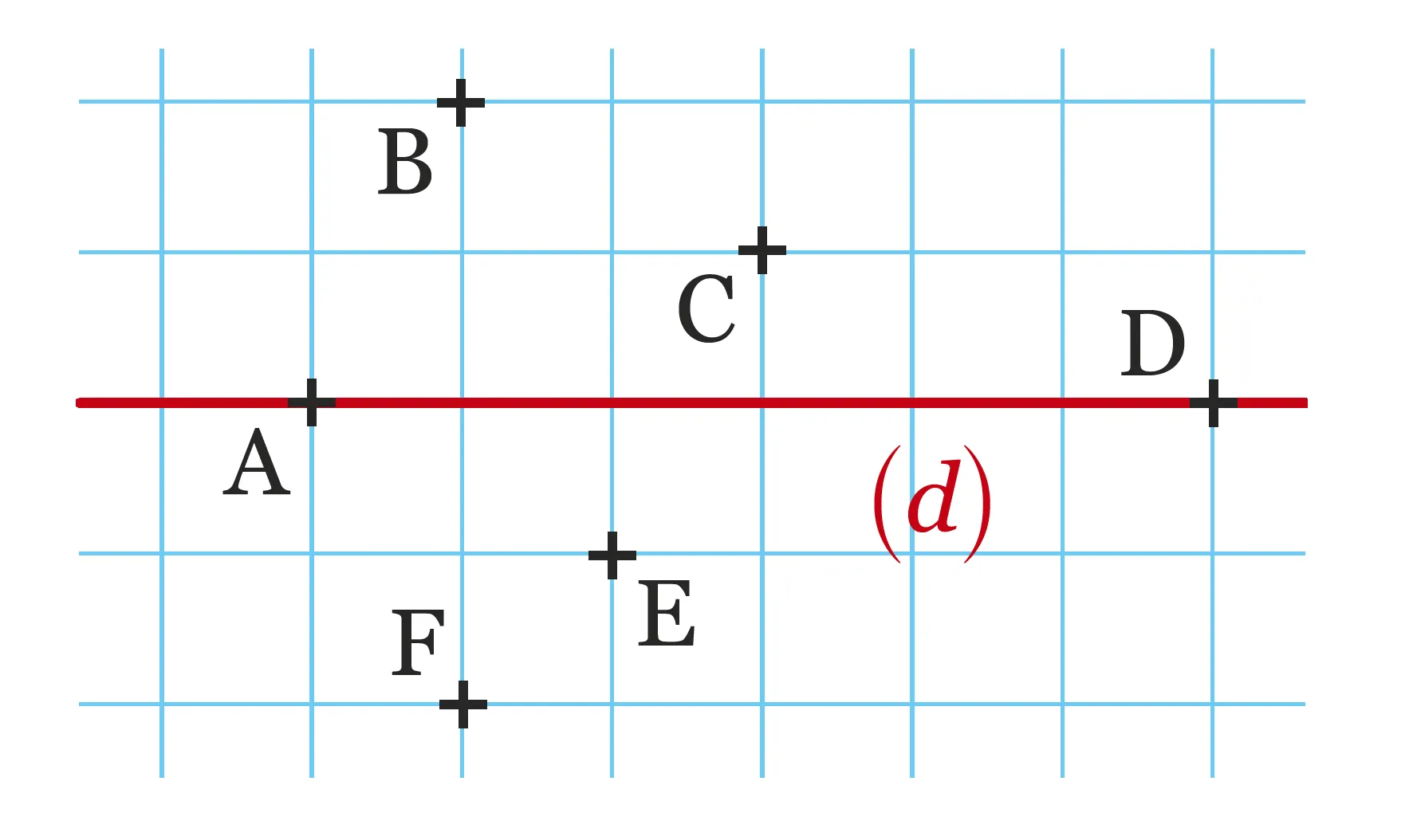
À partir de la figure ci-dessous,
nommer si possible le symétrique de
chaque point par rapport à la droite (d).



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46À l'oral
À l'oral
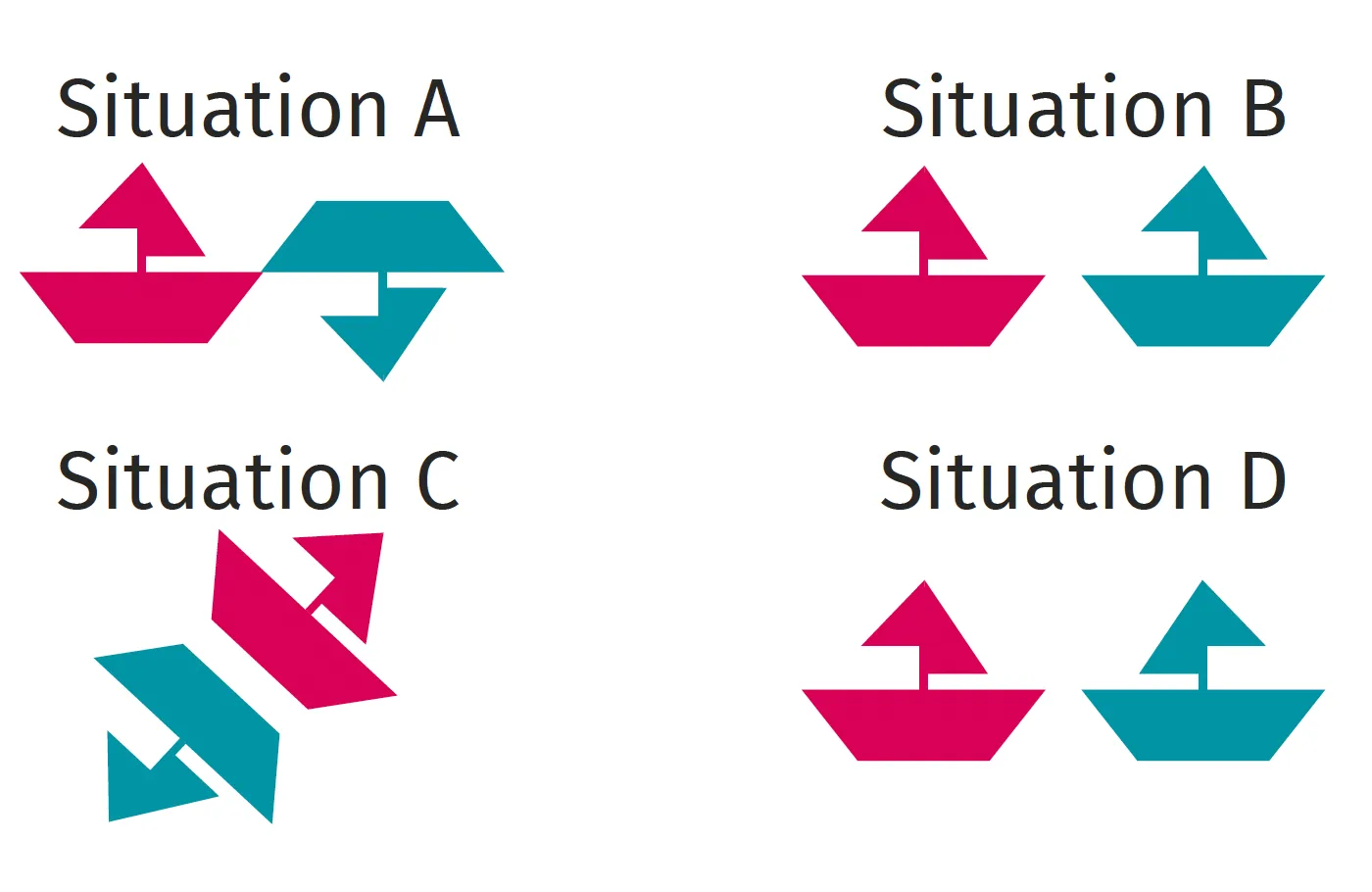
Dans quelles situations les deux
bateaux sont-ils symétriques par rapport
à un axe ? Justifier.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47À l'oral
À l'oral
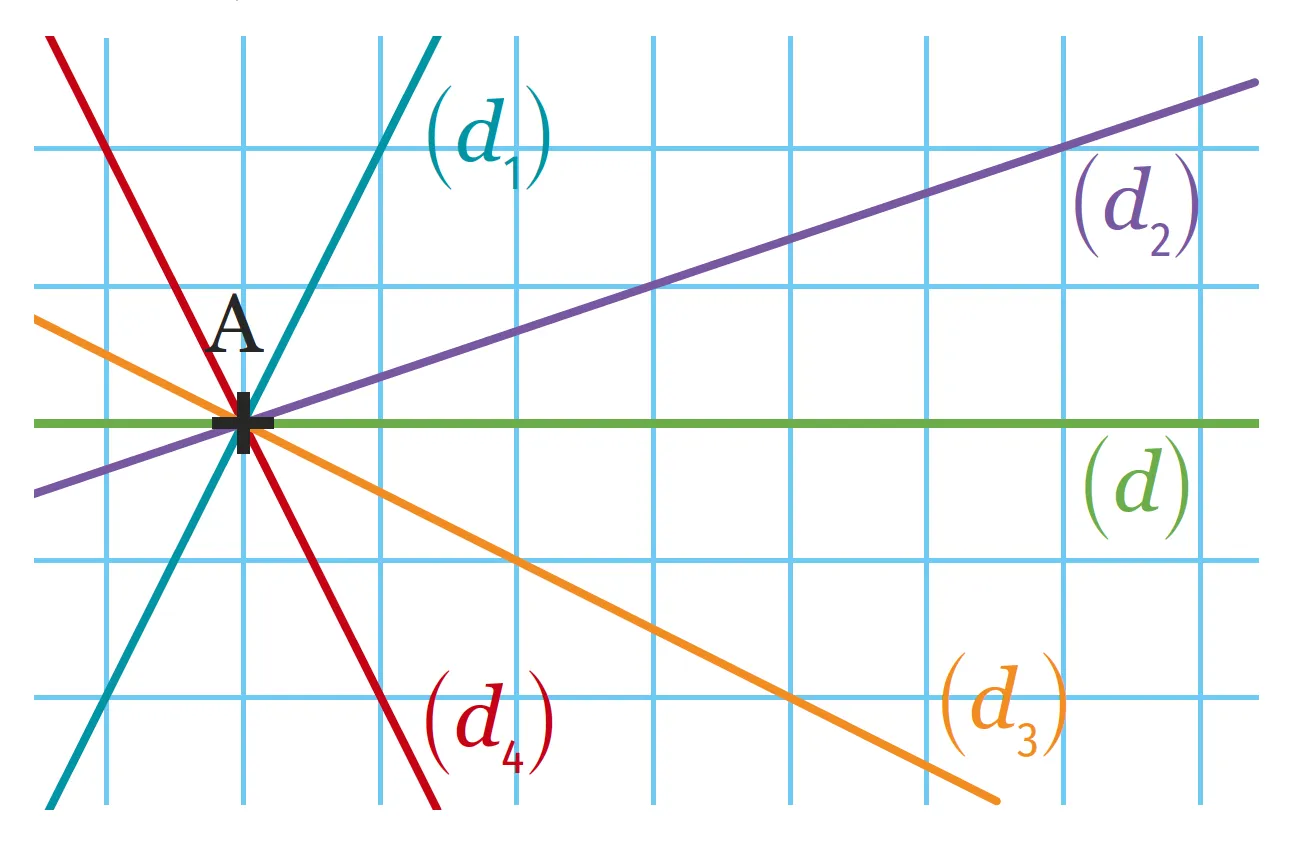
Quelle est la droite symétrique de la
droite \left(d_1\right) par rapport à la droite (d) ?



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
1. Tracer une droite (d) et placer un
point \text {M} en dehors de cette droite.
2. Construire le symétrique de \text {M} par rapport à (d).
2. Construire le symétrique de \text {M} par rapport à (d).
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
Dans cet appartement, quels sont les
éléments symétriques ?




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour les exercices à , les figures sont à .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
On considère la figure ci-dessous.

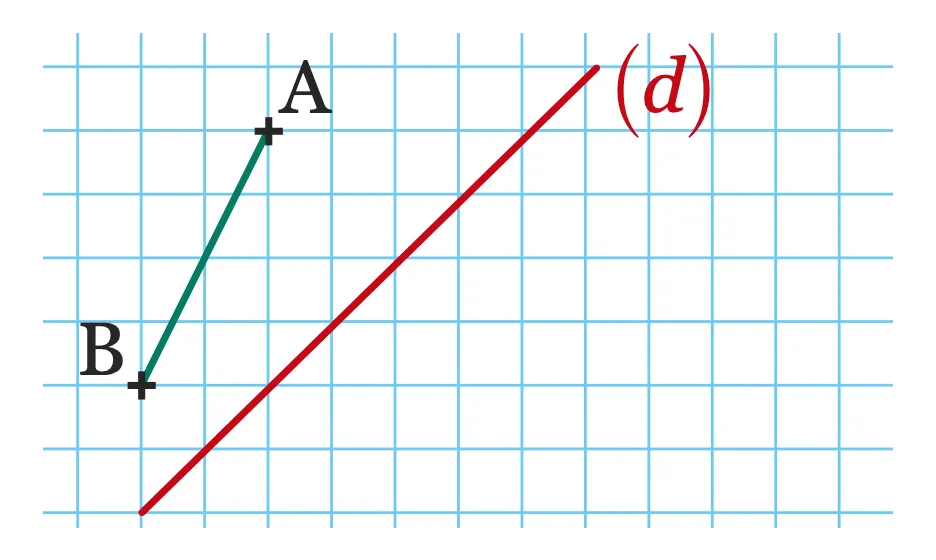
1. Construire le symétrique du segment \text {[AB]} par rapport à la droite (d).
2. Construire le symétrique de la droite (d) par rapport à la droite \mathrm{(AB)}.


1. Construire le symétrique du segment \text {[AB]} par rapport à la droite (d).
2. Construire le symétrique de la droite (d) par rapport à la droite \mathrm{(AB)}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
Générateur d'exercices
Générateur d'exercices
Construire l'image de chaque figure
par symétrie par rapport à la droite (d).

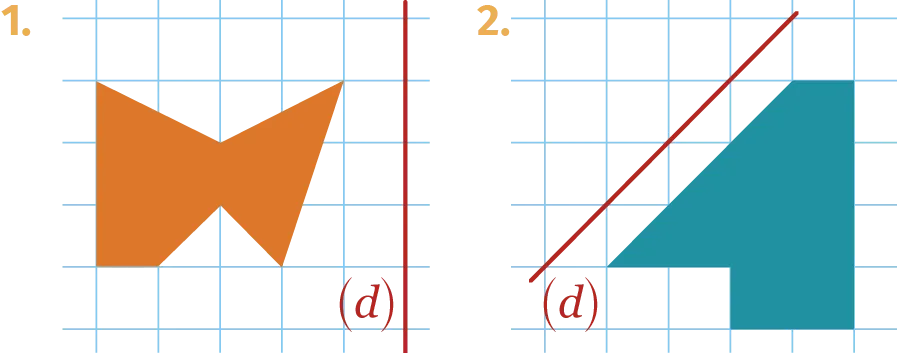

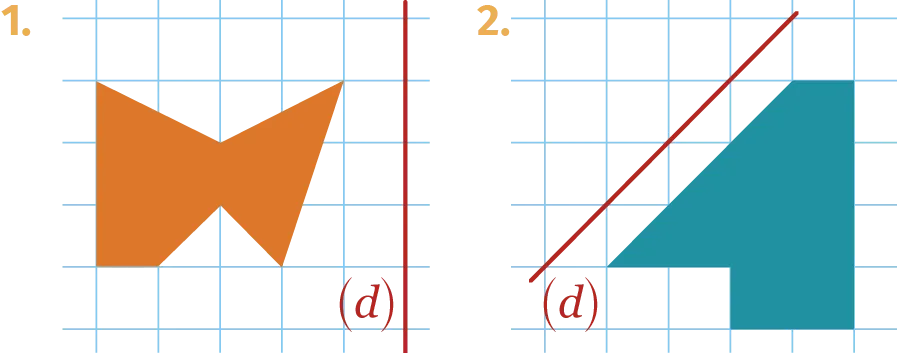
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
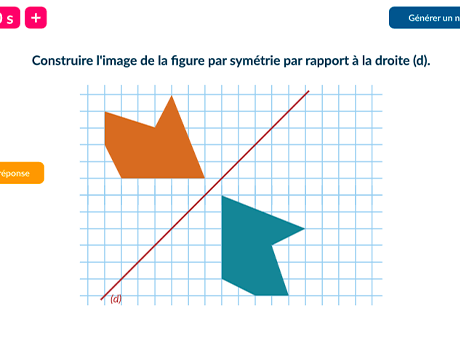
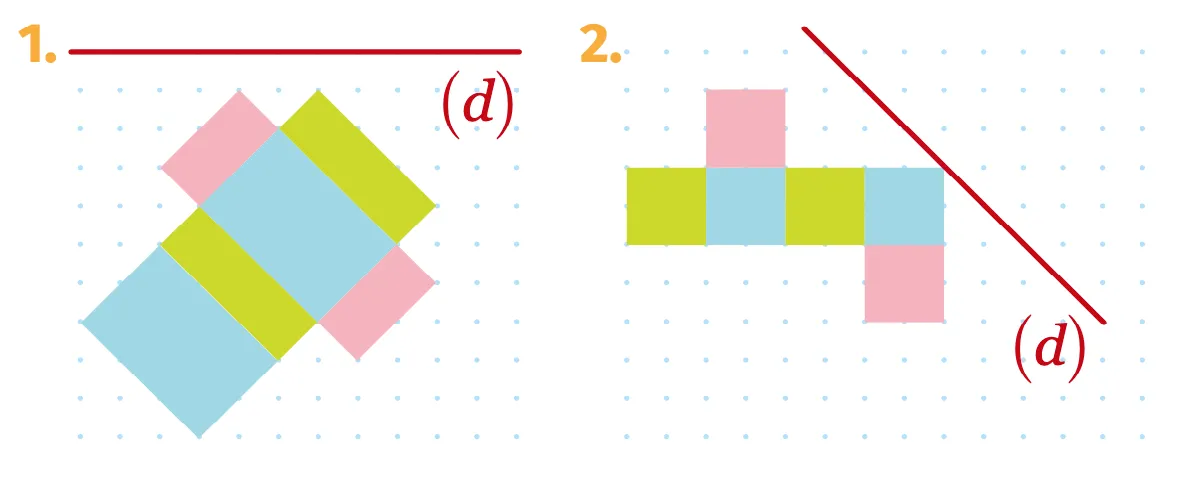
Construire l'image de chaque figure par
symétrie par rapport à la droite (d).



Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
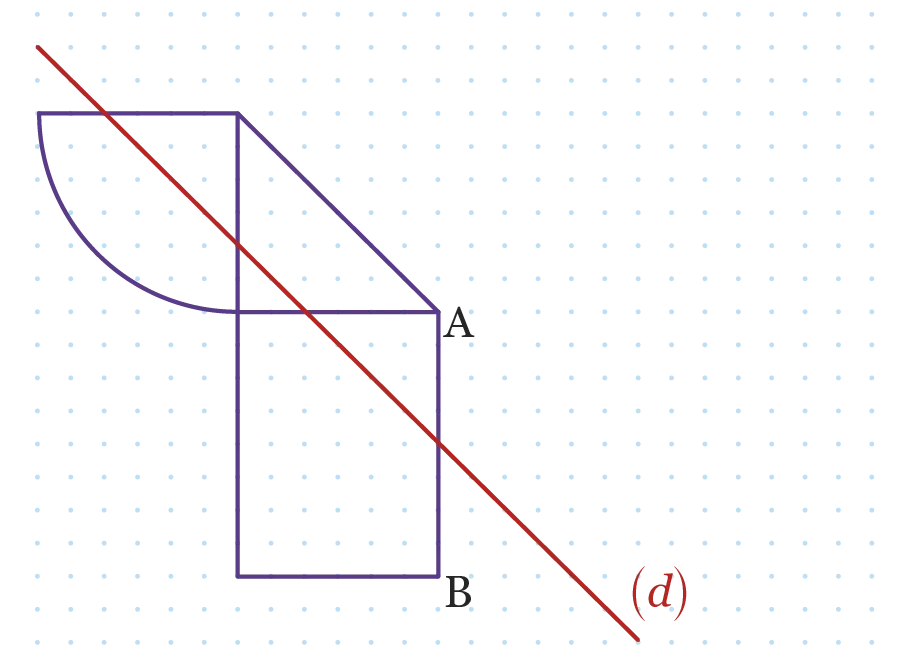
Construire la figure symétrique à la
figure ci-dessous par rapport à la droite (d).



Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
Construire le symétrique du point \text {A}
par rapport à (d).

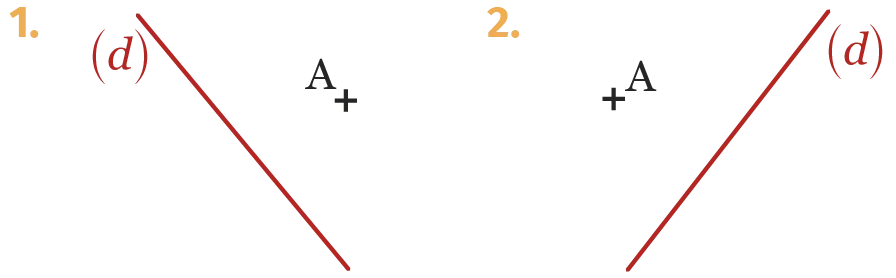

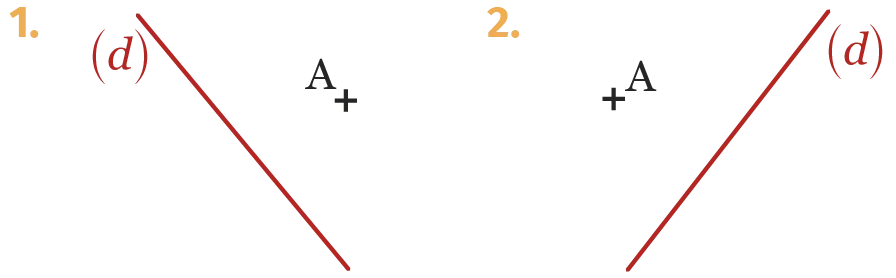
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
Construire la droite symétrique de (\Delta)
par rapport à (d), puis la droite symétrique
de (d) par rapport à (\Delta).

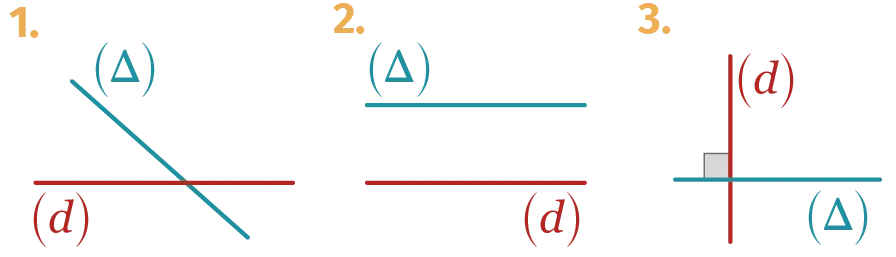

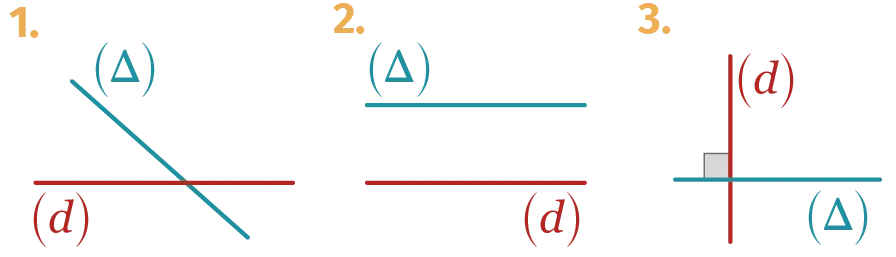
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
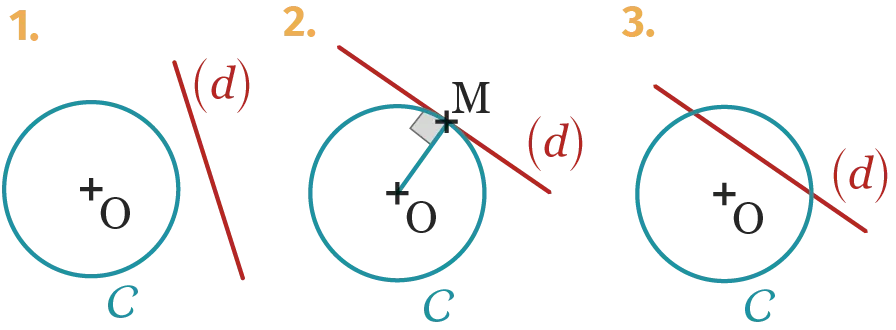
56
Construire le symétrique du cercle C par
rapport à (d).



Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57Copie d'élève
Copie d'élève
Mei a tracé sur son cahler le
symétrique du polygone \text {ABCDE} par rapport
à la droite (d).

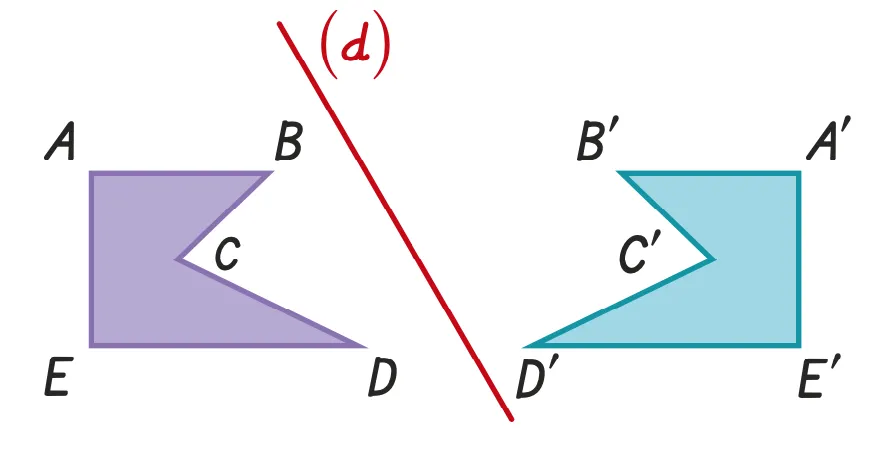
1. Corriger son travail
2. Les deux figures sont quand même
symétriques par rapport à une droite non
tracée. Comment trouver cette droite ?


1. Corriger son travail
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
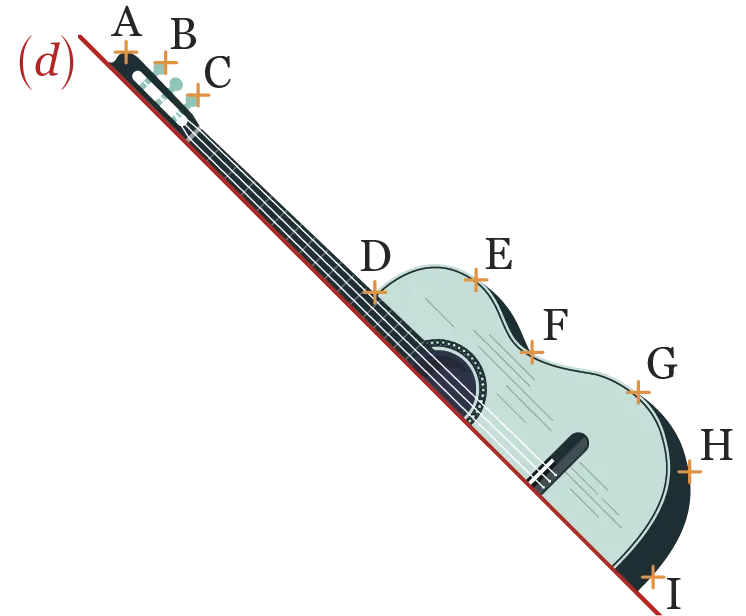
58
Tracer précisément le symétrique de
tous les points indiqués sur la figure par
rapport à la droite (d), puis terminer le
dessin à main levée.



Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
Réaliser le programme de construction
suivant.
- Tracer un segment [\mathrm{AB}] de longueur 5 \mathrm{~cm}.
- Placer un point \text {C} à égale distance de \text {A} et \text {B} tel que \mathrm{AC}=6 \mathrm{~cm}.
- Tracer le cercle de centre \text {P} et de rayon 2 \mathrm{~cm}.
- Tracer le symétrique de ce cercle par rapport à la droite (\mathrm{AB}).
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
Dans le palais de l'Alhambra situé à
Grenade, en Espagne, on peut observer une
décoration à base de carreaux de faïence
colorés, appelés azulejos, ornés de motifs
géométriques.
Donner le numéro des figures symétriques par rapport à chacune des droites. Par exemple, les figures 3 et 7 sont symétriques par rapport à la droite (d_1).


Donner le numéro des figures symétriques par rapport à chacune des droites. Par exemple, les figures 3 et 7 sont symétriques par rapport à la droite (d_1).


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
Les deux figures \mathrm{MATHS} et \mathrm{MOBIL} sont
symétriques par rapport à la droite (d).

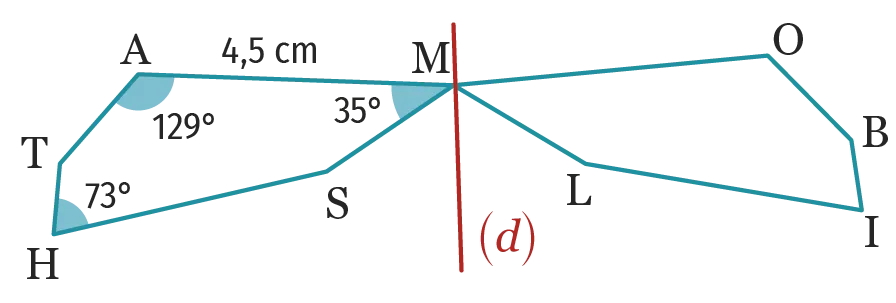


1. Compléter les phrases
suivantes. Par rapport à (d) :
a. le symétrique du point \mathrm{M} est...
b. le symétrique du segment \text {[TH]} est...
c. le symétrique du segment \text {[OB]} est...
d. le symétrique de l'angle \widehat{\mathrm{TAM}} est...
e. le symétrique de l'angle \widehat{\mathrm{LMO}} est...
a. le symétrique du point \mathrm{M} est...
2. Quelle est la longueur du segment \text {[MO]} ?
3. Quelle est la mesure de l'angle \widehat{\mathrm{LIB}} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
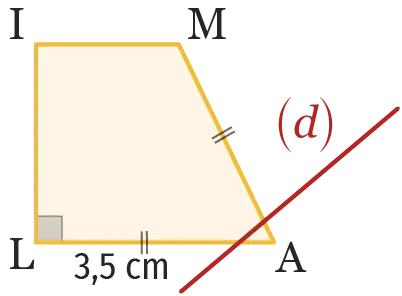
62
Sur la figure suivante, on note \mathrm{I^{\prime}}, \mathrm{M^{\prime}},
\mathrm{A^{\prime}} et \mathrm{L^{\prime}} les symétriques respectifs de \mathrm{I}, \mathrm{M}, \mathrm{A}
et \mathrm{L} par rapport à la droite (d).
Sans construire le quadrilatère \mathrm{L^{\prime} \mathrm{I}^{\prime} \mathrm{M}^{\prime} \mathrm{A}^{\prime}}, donner la mesure du segment \mathrm{\left[\mathrm{M}^{\prime} \mathrm{A}^{\prime}\right]} et de l'angle \mathrm{\widehat{I^{\prime} \mathrm{L}^{\prime} A^{\prime}}}.
Sans construire le quadrilatère \mathrm{L^{\prime} \mathrm{I}^{\prime} \mathrm{M}^{\prime} \mathrm{A}^{\prime}}, donner la mesure du segment \mathrm{\left[\mathrm{M}^{\prime} \mathrm{A}^{\prime}\right]} et de l'angle \mathrm{\widehat{I^{\prime} \mathrm{L}^{\prime} A^{\prime}}}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
1. Construire un angle \widehat{ABC} qui mesure 35^\circ.
2. Construire le point \mathrm{D}, symétrique du point \mathrm{C} par rapport à la droite \mathrm{(AB)}.
3.
a. Quelle est la mesure de l'angle \widehat{ABD} ?
Justifier.
b. Que peut-on dire de la demi-droite \left[\mathrm{BA}\right) ?
Justifier.
2. Construire le point \mathrm{D}, symétrique du point \mathrm{C} par rapport à la droite \mathrm{(AB)}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
Générateur d'exercices
Générateur d'exercices
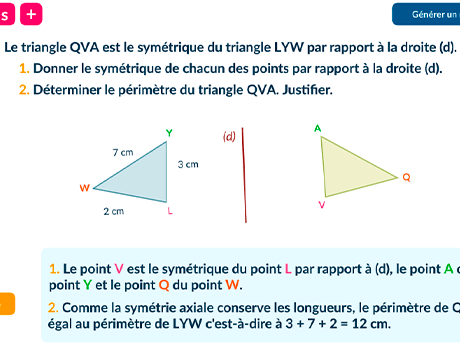
Le rectangle \mathrm{MATH} est le symétrique du
rectangle \mathrm{LYON} par rapport à la droite (d).

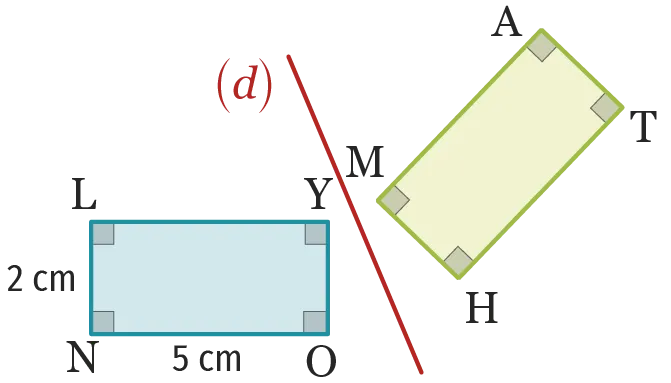
1. Donner le symétrique de chacun des points par rapport à la droite (d).
2. Déterminer le périmètre du rectangle
\mathrm{MATH}. Justifier.


1. Donner le symétrique de chacun des points par rapport à la droite (d).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
Voici une figure réalisée par origami.
Les points marqués de la même couleur sont
symétriques par rapport à (d).

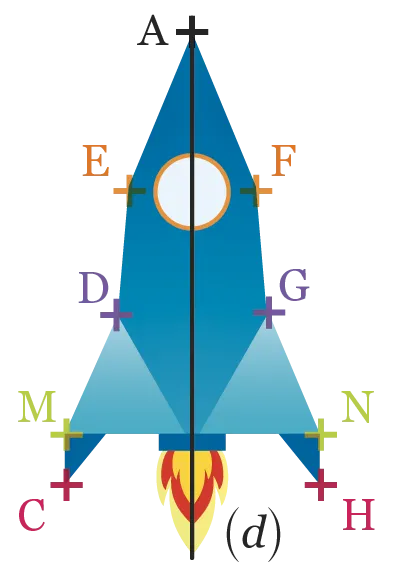
1. Citer deux longueurs égales.
2. Citer deux angles de même mesure.
3. Donner le symétrique du segment \mathrm{[DM]}.
4. Donner le symétrique de l'angle \widehat{\mathrm{CMD}}.


1. Citer deux longueurs égales.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille