Mathématiques 6e - 2025
Mes Pages
Rappels de primaire
Chapitre 1
Nombres entiers
Chapitre 2
Notion de fraction
Chapitre 3
Opérations sur les fractions
Chapitre 4
Nombres décimaux
Chapitre 5
Demi-droites graduées
Chapitre 6
Addition, soustraction, multiplication
Chapitre 7
Divisions
Chapitre 8
Organisation et gestion de données
Chapitre 9
Proportionnalité
Chapitre 10
Durées
Chapitre 11
Probabilités
Chapitre 12
Droites et segments
Chapitre 13
Angles
Chapitre 14
Cercles et disques
Chapitre 15
Symétrie axiale
Chapitre 16
Triangles
Chapitre 17
Entrée en matière
Aires et volumes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLes unités de mesure
Jusqu'au XVIIIe siècle, les unités de mesure se
rapportaient souvent à des parties du corps
humain : la coudée, la palme, le doigt, le
pied, le pouce, etc., et cela causait beaucoup
d'imprécisions de mesures.
C'est en 1791, après la Révolution française, que le mètre est défini. Sa création avait pour but d'harmoniser les unités de longueur et ce fut une réussite : aujourd'hui, seulement six pays dans le monde ne l'utilisent pas au quotidien !
L'unité d'aire usuelle est donc le mètre carré (m²). En France, on utilise aussi une unité dérivée du mètre carré pour mesurer de grandes surfaces : l'are (a). On rencontre plus souvent l'hectare (ha) : 1 \mathrm{ha} = 100 \mathrm{a} = 10 000 \mathrm{m²}.
C'est en 1791, après la Révolution française, que le mètre est défini. Sa création avait pour but d'harmoniser les unités de longueur et ce fut une réussite : aujourd'hui, seulement six pays dans le monde ne l'utilisent pas au quotidien !
L'unité d'aire usuelle est donc le mètre carré (m²). En France, on utilise aussi une unité dérivée du mètre carré pour mesurer de grandes surfaces : l'are (a). On rencontre plus souvent l'hectare (ha) : 1 \mathrm{ha} = 100 \mathrm{a} = 10 000 \mathrm{m²}.
Mètre étalon place Vendôme, Paris.
Combien d'hectares mesure un terrain de \bold{25 000 }\mathrm{\bold{m²}} ?
Supplément numérique
Retrouvez cette histoire en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
Lorsque l'on veut réaliser des travaux de peinture, on a
besoin d'estimer la quantité de peinture à acheter. Cela se
fait en deux étapes.
Tout d'abord, il faut calculer la surface totale à peindre grâce aux formules de géométrie. Ensuite, il faut calculer le volume de peinture nécessaire pour recouvrir cette surface. Pour cela, on se réfère au rendement indiqué sur le pot, qui indique quelle surface on peut peindre avec 1 \mathrm{L} de peinture. On fait alors un calcul de proportionnalité !
Tout d'abord, il faut calculer la surface totale à peindre grâce aux formules de géométrie. Ensuite, il faut calculer le volume de peinture nécessaire pour recouvrir cette surface. Pour cela, on se réfère au rendement indiqué sur le pot, qui indique quelle surface on peut peindre avec 1 \mathrm{L} de peinture. On fait alors un calcul de proportionnalité !
Pour peindre deux couches sur les deux faces de dix portes rectangulaires de longueur \bold{2 \mathrm{\bold{m}}} et de largeur \bold{0,85 \mathrm{\bold{m}}} avec la peinture suivante, combien de pots de \bold{3 \mathrm{\bold{L}}} doit-on acheter ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Convertir des unités de mesure d'aire
1. Tracer un carré de côté 1 \mathrm{dm}. Quelle est la mesure de l'aire de ce carré exprimée en dm² ?
2. Sur chaque côté du carré, placer une graduation tous les centimètres. Combien de centimètres y a-t-il sur chaque côté ?
Cliquez pour accéder à GeoGebra
GeoGebra
2. Sur chaque côté du carré, placer une graduation tous les centimètres. Combien de centimètres y a-t-il sur chaque côté ?
3. Relier les graduations deux à deux : chaque graduation est reliée avec celle qui lui fait face.
On obtient une grille. Combien de cases carrés de côté 1 \mathrm{cm} obtient-on dans cette grille ?
4. Quelle est l'aire de chacun de ces petits carrés?
Convertir \bold{1 \mathrm{\bold{dm²}}} en \bold{1 \mathrm{\bold{cm²}}}. Comment convertir \bold{1 \mathrm{\bold{m²}}} en \bold{1 \mathrm{\bold{dm²}}} ?
Bilan
Convertir \bold{1 \mathrm{\bold{dm²}}} en \bold{1 \mathrm{\bold{cm²}}}. Comment convertir \bold{1 \mathrm{\bold{m²}}} en \bold{1 \mathrm{\bold{dm²}}} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Représenter un assemblage
On considère le solide suivant formé par un assemblage de cubes
identiques.
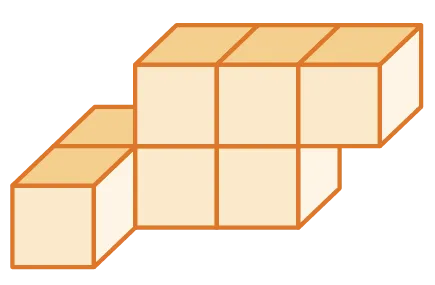
2. Représenter sur une feuille à carreaux la vue gauche et la vue du dessus de l'assemblage.
Cliquez pour accéder à GeoGebra
GeoGebra
Bilan
Comment peut-on représenter un assemblage de cubes sur le plan ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationCalculer un volume
Pour réaliser cette activité, prévoir 24 cubes par groupe d'élèves.
Un cube est l'unité de volume.
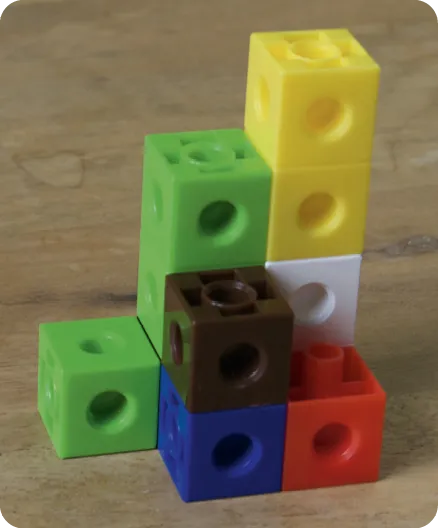
Un cube est l'unité de volume.
1. a. Combien a-t-on utilisé de cubes pour réaliser la construction ? Réaliser cette construction pour vérifier.
b. En déduire le volume de la construction.
2. On souhaite utiliser les cubes restants pour compléter la
construction et former un pavé droit.
a. Combien de cubes sont nécessaires, en tout, pour construire le pavé droit commencé ? Ce nombre est le volume du pavé droit.
b. Réaliser alors la construction complète pour vérifier.
Vérifier que le volume du pavé droit est égal à \bold{2 × 3 × 4}. Comment peut-on expliquer ce calcul ?
a. Combien de cubes sont nécessaires, en tout, pour construire le pavé droit commencé ? Ce nombre est le volume du pavé droit.
Cliquez ici pour avoir accès à un espace de dessin
Bilan
Vérifier que le volume du pavé droit est égal à \bold{2 × 3 × 4}. Comment peut-on expliquer ce calcul ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
