Chapitre 2
Activité
Découvrir le chapitre : Calcul numérique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Petit voyage en Égypte
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie A : L'œil d'Horus
Dans la mythologie égyptienne, on raconte qu'Horus eut son œil arraché par son oncle Seth.
Ce dernier coupa alors son œil en six parties comme représenté ici.
Ce dernier coupa alors son œil en six parties comme représenté ici.

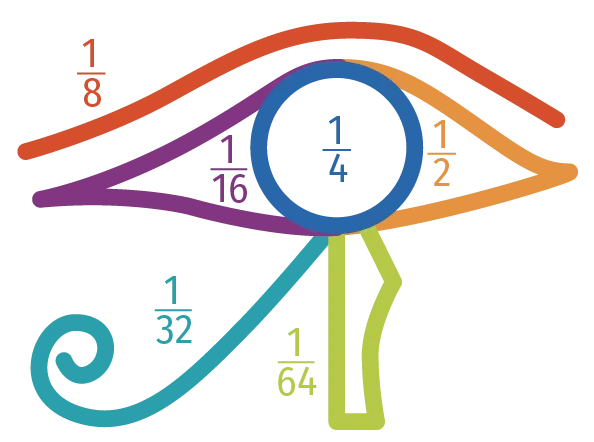
Horus est une divinité égyptienne. Il était représenté par un homme à tête de faucon.
1
Donner deux points communs entre toutes les fractions
représentées.
2
Donner l'écriture fractionnaire de leur somme.
3
Quelle fraction faut‑il ajouter à cette somme pour obtenir 1 ?
Partie B : Fractions égyptiennes
Une fraction égyptienne est une fraction dont le numérateur est 1. On admet que toutes les fractions peuvent s'écrire comme la somme de fractions égyptiennes de valeurs différentes.
1
Calculer les sommes \frac{1}{4}+\frac{1}{10} et \frac{1}{2}+\frac{1}{22}.
2
On souhaite maintenant décomposer des fractions en somme de fractions égyptiennes distinctes. Pour cela, on peut multiplier le numérateur et le dénominateur par 2. Par exemple {\frac{5}{9}=\frac{5 \times 2}{9 \times 2}=\frac{10}{18}=\frac{9+1}{18}=\frac{9}{18}+\frac{1}{18}=\frac{1}{2}+\frac{1}{18}}. En raisonnant de la même manière, décomposer \frac{3}{5} et \frac{2}{3}.
Bilan
Peut‑on appliquer la méthode de la partie B à toutes les fractions ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Distance entre les planètes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce tableau donne les distances, en kilomètre, entre les différentes planètes et le Soleil.
| Jupiter | 778{,}5 millions |
| Mars | 227\:900\:000 |
| Mercure | 57{,}91 \times 10^{6} |
| Neptune | 4{,}495 milliards |
| Saturne | 1\:434\:000\:000 |
| Terre | 149\:600 milliers |
| Uranus | 2{,}871 \times 10^{9} |
| Vénus | 108{,}2 millions |
1
Écrire chacune des distances sous forme décimale.
2
Écrire chacune des distances sous la forme a \times 10^{n}, avec 1 \leqslant a \lt10 et n un nombre entier.
Bilan
Toutes ces distances ont été exprimées de deux manières différentes. Quel est l'avantage de la seconde écriture par rapport à la première ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 3Le triangle de Sierpiński
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des maths
Wacław Sierpiński est un mathématicien polonais (1882‑1969) qui a notamment travaillé sur la théorie des ensembles, la théorie des nombres, la théorie des fonctions et la topologie. Une autre fractale célèbre porte son nom : le tapis de Sierpiński.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une fractale est un objet qui se répète à l'infini. En zoomant sur une partie, le tout réapparaît à l'identique.
Nous allons nous intéresser à la construction d'une fractale particulière : le triangle de Sierpiński.
Voici les différentes étapes à suivre pour construire le triangle de Sierpiński.
Étape 0 : On trace un triangle équilatéral.
Étape 1 : On trace le triangle blanc ayant pour sommets les milieux de chacun des côtés du triangle précédent.
Étapes 2 et 3 : On réitère ce procédé avec chacun des triangles roses obtenus, comme ci‑dessous.


1
Construire le triangle de Sierpiński de l'étape 2 en prenant pour triangle de départ un triangle équilatéral de côté 8 cm.
2
Compléter le tableau suivant.
| Étape n° | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Nombre de triangles roses |
3
Si on poursuit la construction jusqu'à l'étape 5, déterminer le nombre de triangles roses obtenus.
4
Déborah affirme qu'à l'étape 10, il y a 3^{10} triangles roses. A‑t‑elle raison ?
Bilan
Conjecturer le nombre de triangles roses à l'étape {n}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

