Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Chapitre 6
Travailler autrement
Activité différenciée
11 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Introduction
En quoi consiste le cryptage affine ?
- Chaque lettre d'un message est codée par son rang dans l'alphabet (A correspond au rang 0, B au rang 1, etc.). On calcule l'image de ces nombres par une fonction affine {f: x \mapsto a x+b}.
- On détermine le reste de la division euclidienne de ces images par 26.
- Chaque reste obtenu correspond à une lettre de l'alphabet et on crypte ainsi le message.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parcours 1
1. a. Dans un même repère, tracer les droites (d_1) et (d_2) sachant que :
b. Le paramètre a de la fonction affine f recherchée est l'abscisse du point d'intersection des droites (d_1) et (d_2). Déterminer graphiquement la valeur de a.
2. a. Dans le même repère, tracer la droite (d_3) représentant la fonction {h: x \mapsto \frac{2}{3} x}.
b. Le paramètre b de la fonction affine f recherchée est l'ordonnée du point d'intersection des droites (d_2) et (d_3). Déterminer graphiquement la valeur de b.
3. Donner alors l'expression de la fonction affine f recherchée et crypter le mot « FONCTION ».
- la droite (d_1) est la courbe représentative de la fonction g: x \mapsto 10-x ;
- la droite (d_2) passe par les points \mathrm{A}(-1 \: ; 1) et \mathrm{B}(11 \: ; 4).
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parcours 2
Voici quatre dominos.
1. Trouver la valeur des deux faces des quatre dominos puis les placer correctement à la suite d'un domino bleu déjà placé.
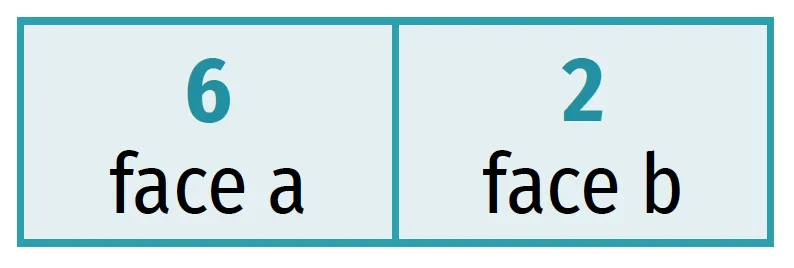
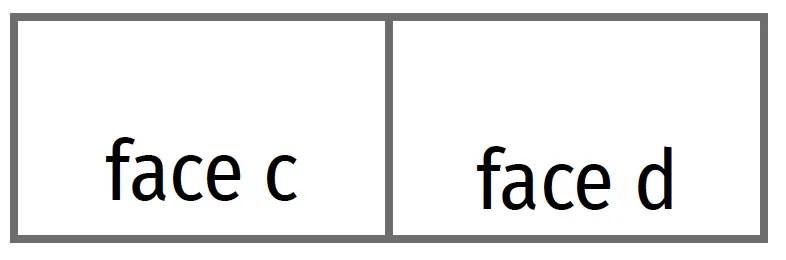
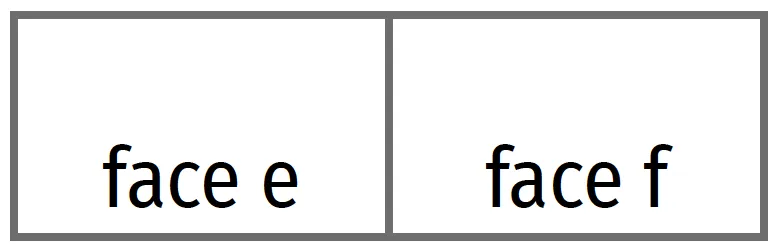
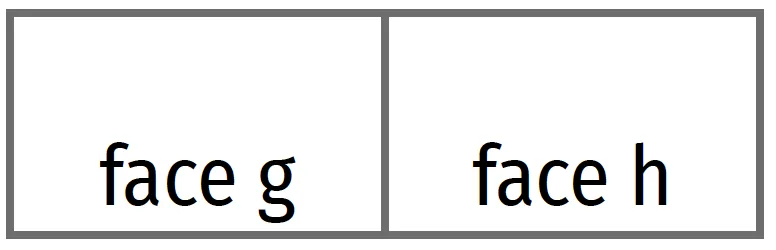
2. a. Le coefficient a de la fonction affine f recherchée est la somme des faces a, c, g et i.
b. Le coefficient b de la fonction affine f recherchée est la différence positive des faces d et h.
3. Donner alors l'expression de la fonction affine f recherchée et crypter le mot « FONCTION ».
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
1. Trouver la valeur des deux faces des quatre dominos puis les placer correctement à la suite d'un domino bleu déjà placé.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah