Dossier
Rappels
Rappels
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calcul littéral
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Une expression littérale est une expression dans laquelle des lettres représentent des nombres dont on ne connaît pas la valeur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
3 y+8 et 4 a(2-b) sont des expressions littérales.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Il n'est pas nécessaire d'écrire le signe \times lorsqu'il est situé avant une lettre ou avant une parenthèse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
3 \times a \times b=3 a b
(2-x) \times 4=4 \times(2-x)=4(2-x)
(1-2 \times x) \times(x-5)=(1-2 x)(x-5)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On peut calculer les différentes valeurs d'une expression littérale en remplaçant la lettre par un nombre choisi.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
Si x=2 alors l'expression 3 x+8 vaut {3 \times 2+8=6+8=14}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On peut simplifier l'écriture d'une expression littérale en modifiant l'ordre des facteurs dans un produit.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
3 x \times 2=2 \times 3 x=6 x
4 x \times 2 x=4 \times 2 \times x \times x=8 x^{2}
(2 x)^{2}=(2 x) \times(2 x)=2 \times 2 \times x \times x=4 x^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On peut réduire l'écriture d'une expression littérale en regroupant les termes de même nature.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
\begin{aligned} 3 x-2+4 x^{2}-5 x+7 &=4 x^{2}+3 x-5 x-2+7 \\ &=4 x^{2}-2 x+5 \end{aligned}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Développer c'est transformer un produit en somme.
❯ Factoriser c'est transformer une somme en produit.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
8 x-4 x^{2} est la forme développée de {4 x(2-x)} qui est une forme factorisée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Propriété de la simple distributivité : Quels que soient les nombres k, a et b, on a : k(a+b)=k a+k b et k(a-b)=k a-k b.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
3 \times(-2+x)=3 \times(-2)+3 \times x=-6+3 x
4 x(2-x)=4 x \times 2-4 x \times x=8 x-4 x^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Pour développer et réduire une expression littérale, on commence par développer en utilisant la simple distributivité, puis on simplifie les produits pour enfin réduire la somme obtenue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
\begin{aligned} 3 x-2 x(5 x-1) & =3 x-2 x \times 5 x-2 x \times(-1) \\ & =3 x-10 x^{2}+2 x \\ & =5 x-10 x^{2} \end{aligned}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Pour factoriser une expression littérale, on peut identifier un facteur commun puis utiliser la simple distributivité : {k a+k b=k(a+b)} ou {k a-k b=k(a-b).}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
6+3 x={\color{firebrick}3} \times 2+{\color{firebrick}3} \times x={\color{firebrick}3}(2+x)
5 x-10 x^{2}={\color{teal}5 x} \times 1-2 x \times {\color{teal}5 x}={\color{teal}5 x}(1-2 x)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Une équation est une égalité dans laquelle figurent une ou plusieurs inconnues.
❯ Les solutions d'une équation sont toutes les valeurs de l'inconnue pour lesquelles l'égalité est vérifiée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Une solution de l'équation 3 x-1=5 est {x=2} car 3 \times 2-1=5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Deux grandeurs sont proportionnelles si l'on obtient les valeurs de l'une en multipliant les valeurs de l'autre par un même nombre, appelé le coefficient de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans une boucherie, le prix à payer pour l'achat de merguez est proportionnel à la masse de merguez achetée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On représente les situations de proportionnalité dans un tableau de proportionnalité en y ajoutant le coefficient de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
En reprenant l'exemple ci-dessus :
| Masse (en kg) | 1 | 1{,}5 | ⤸\times 8 |
| Prix (en €) | 8 | {\color{firebrick}12} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Grâce au coefficient de proportionnalité, on peut déterminer des valeurs inconnues dans un tableau de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans l'exemple ci-dessus, 3{,}5 kg de merguez coûtent 3{,}5 \times 8 = 28 €.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On peut aussi déterminer des valeurs inconnues en multipliant les valeurs des colonnes par un même nombre ou en ajoutant les valeurs de colonnes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
4{,}5 kg coûtent 12 \times 3 = 36 €. 6 kg coûtent 12 + 36 = 48 €.
\stackrel{\times 3}{\curvearrowright} | ||
| Masse (en kg) | 1{,}5 | 4{,}5 |
| Prix (en €) | 12 | \color{firebrick}36 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
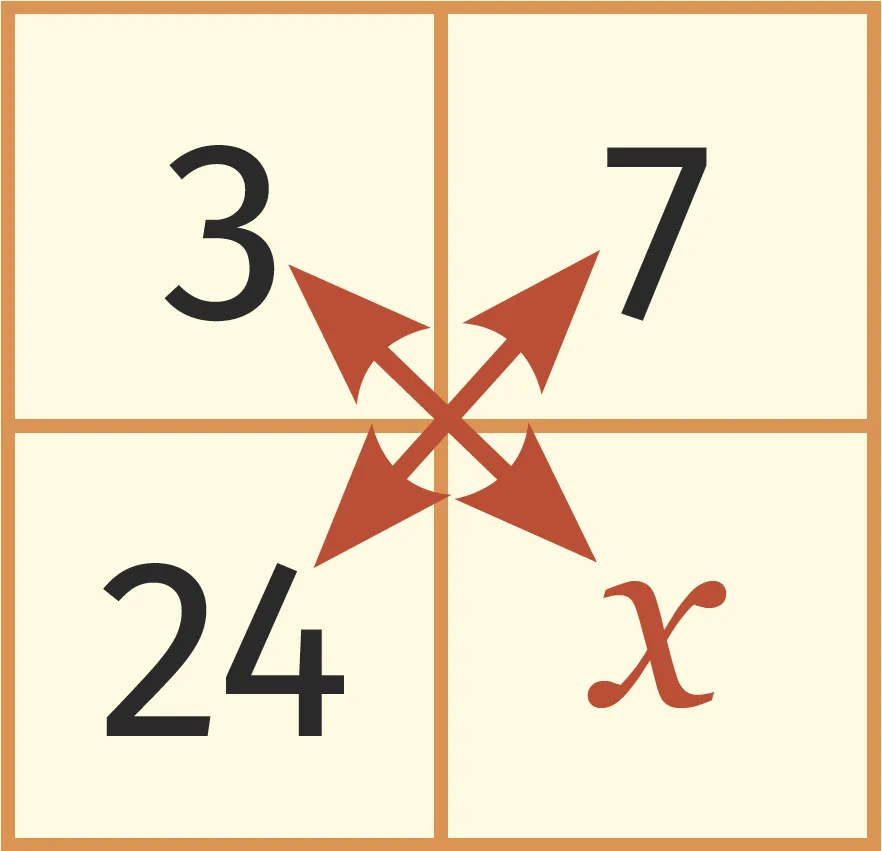
❯ L'égalité des produits en croix peut être utilisée pour déterminer une valeur inconnue dans un tableau de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On a 3 \times x=24 \times 7 donc x=\frac{24 \times 7}{3}=\frac{168}{3}=56

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Statistiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On peut regrouper les valeurs identiques d'une série en dressant un tableau des effectifs. Les effectifs indiquent le nombre de fois où apparaît la valeur dans la série.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On peut représenter la série -1 \:; 2 \:; - 1 \:; 2 \:; 0 \:; 2 par le tableau suivant.
| Valeurs | -1 | 0 | 2 |
| Effectifs | 2 | 1 | 3 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ La fréquence d'une valeur se calcule avec la formule :
\textbf{fréquence} = \dfrac{\textbf{effectif de la valeur}} {\textbf{effectif total}}.
La somme de toutes les fréquences est égale à 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans le tableau ci-dessus, l'effectif total vaut 2 + 1 + 3 = 6 donc la fréquence de la valeur 2 est \frac{3}{6}=0{,}5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On exprime souvent les fréquences en pourcentage, c'est-à-dire une fraction dont le dénominateur est 100.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La fréquence ci-dessus vaut 0{,}5=\frac{50}{100}. Il y a 50 % de 2 dans la série.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème de Pythagore
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Dans un triangle rectangle, on peut appliquer le théorème de Pythagore : le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans le triangle \text{ABC} rectangle en \text{A}, on applique le théorème de Pythagore : {\mathrm{BC}^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2}}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Dans un triangle rectangle, on peut calculer une longueur inconnue si on connaît les deux autres longueurs. Il suffit de remplacer, dans les membres de l'égalité, les longueurs par celles qui sont connues. On cherche ci‑contre la longueur de l'hypoténuse (le côté opposé à l'angle droit).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
\begin{array}{l}
\mathrm{BC}^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2} \\
\mathrm{BC}^{2}=3^{2}+2^{2}=13
\end{array}
Donc \mathrm{BC}=\sqrt{13}.
Donc \mathrm{BC}=\sqrt{13}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On cherche ci-contre la longueur d'un des côtés de l'angle droit. Si on souhaite donner une valeur approchée, on peut utiliser la touche \sqrt{\boxed{}} de la calculatrice.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
\begin{array}{l}
\mathrm{BC}^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2} \\
4^{2}=3^{2}+\mathrm{AC}^{2} \\
16=9+\mathrm{AC}^{2}
\end{array}
ainsi \mathrm{AC}^{2}=16-9=7
donc \mathrm{AC}=\sqrt{7} \approx 2{,}6.
ainsi \mathrm{AC}^{2}=16-9=7
donc \mathrm{AC}=\sqrt{7} \approx 2{,}6.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ On peut déterminer si un triangle est rectangle ou non quand on connaît les longueurs de ses trois côtés. Pour cela, on vérifie si l'égalité de Pythagore est vraie.
- D'une part, on calcule le carré de la longueur du plus grand côté.
- D'autre part, on calcule la somme des carrés des longueurs des deux autres côtés.
- Si les résultats sont égaux, alors l'égalité de Pythagore est vérifiée donc le triangle est rectangle (on peut préciser en quel sommet). Si les résultats ne sont pas égaux, alors l'égalité de Pythagore n'est pas vérifiée donc le triangle n'est pas rectangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
1. [\mathrm{GE}] est le plus grand côté.
D'une part,
\mathrm{G E}^{2}=5^{2}=25.
D'autre part,
\mathrm{GF}^{2}+\mathrm{FE}^{2}=3^{2}+4^{2}=25.
Comme \mathrm{GE}^{2}=\mathrm{GF}^{2}+\mathrm{FE}^{2},
alors l'égalité de Pythagore
est vérifiée.
Le triangle \text{GFE} est donc
rectangle en \text{F}.
D'une part,
\mathrm{G E}^{2}=5^{2}=25.
D'autre part,
\mathrm{GF}^{2}+\mathrm{FE}^{2}=3^{2}+4^{2}=25.
Comme \mathrm{GE}^{2}=\mathrm{GF}^{2}+\mathrm{FE}^{2},
alors l'égalité de Pythagore
est vérifiée.
Le triangle \text{GFE} est donc
rectangle en \text{F}.

2. [\mathrm{BC}]est le plus grand
côté.
\begin{array}{l} \mathrm{BC}^{2}=4^{2}=16 \\ \mathrm{AB}^{2}+\mathrm{AC}^{2}=2^{2}+3^{2}=13 . \end{array}
Comme \mathrm{BC}^{2} \neq \mathrm{AB}^{2}+\mathrm{AC}^{2},
alors l'égalité de Pythagore n'est pas
vérifiée. Le triangle \text{ABC} n'est donc
pas rectangle.
\begin{array}{l} \mathrm{BC}^{2}=4^{2}=16 \\ \mathrm{AB}^{2}+\mathrm{AC}^{2}=2^{2}+3^{2}=13 . \end{array}
Comme \mathrm{BC}^{2} \neq \mathrm{AB}^{2}+\mathrm{AC}^{2},
alors l'égalité de Pythagore n'est pas
vérifiée. Le triangle \text{ABC} n'est donc
pas rectangle.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer une aire ou un volume
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ L'aire d'un triangle dont on connaît la longueur c d'un côté et celle de sa hauteur relative h vaut : {\text{A}_{\text {triangle }}=\frac{c \times h}{2}.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
L'aire du triangle \text{ABC} suivant est :
\begin{array}{l} \text{A}=\frac{11 \times 4}{2} \\ \text{A}=22 \mathrm{~cm}^{2}. \end{array}
\begin{array}{l} \text{A}=\frac{11 \times 4}{2} \\ \text{A}=22 \mathrm{~cm}^{2}. \end{array}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Le périmètre d'un cercle de rayon r vaut : \mathrm{P}_{\text {cercle }}=2 \pi r.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ L'aire d'un disque de rayon r vaut : \mathrm{A}_{\text {disque }}=\pi r^{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le périmètre d'un cercle de rayon 5 cm vaut \mathrm{P}=2 \times \pi \times 5 \approx 31{,}4 cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
L'aire d'un disque de diamètre 8 cm vaut {\mathrm{A}=\pi \times 4^{2} \approx 50{,}3} cm2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Le volume d'un cylindre de rayon r et de hauteur h vaut :
\begin{array}{l} \mathrm{V}_{\text {cylindre }}=\mathrm{A}_{\text {base }} \times h \\ \mathrm{~V}_{\text {cylindre }}=\pi r^{2} \times h. \end{array}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le volume du cylindre suivant est :
\begin{array}{l} \mathrm{V}=\pi \times 5^{2} \times 6 \\ \mathrm{~V} \approx 471 \mathrm{~cm}^{3}. \end{array}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Le volume d'un cône de rayon r et de hauteur h vaut :
\begin{array}{l} \mathrm{V}_{\text {cône }}=\frac{\mathrm{A}_{\text {base }} \times h}{3} \\ \mathrm{~V}_{\text {cône }}=\frac{\pi r^{2} \times h}{3}. \end{array}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le volume d'un cône de rayon 4 cm et de hauteur 9 cm est :
\begin{array}{l} \mathrm{V}=\frac{\pi \times 4^{2} \times 9}{3} \\ \mathrm{~V} \approx 151 \mathrm{~cm}^{3} . \end{array}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
❯ Le volume d'une pyramide de hauteur h dont on connaît l'aire de la base vaut :
\mathrm{V}_{\text {pyramide }}=\frac{\mathrm{A}_{\text {base }} \times h}{3}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le volume de la pyramide à base rectangulaire suivant vaut :
\begin{array}{l} \mathrm{V}=\frac{\mathrm{A}_{\text {rectangle }} \times h}{3} \\ \mathrm{~V}=\frac{5 \times 4 \times 7}{3} \\ \mathrm{~V} \approx 46,7 \mathrm{~cm}^{3} . \end{array}

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

