Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 2
L'essentiel
Fonctions de la variable réelle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiche méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Analyser une représentation graphique
- La courbe représentative d'une fonction f est formée par l'ensemble des points de coordonnées (x~; f(x)), où x \in \mathrm{D}.
- Le point de coordonnées (x~;y) appartient à la courbe représentative de f si, et seulement si, y=f(x).
- L'ensemble de définition de f se lit sur l'axe des abscisses.
- Les images f(x) se lisent sur l'axe des ordonnées.
- Les antécédents et les solutions d'(in)équations se lisent sur l'axe des abscisses.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Étudier des fonctions du type \boldsymbol{x \mapsto a x^{2}+c}, \boldsymbol{a \neq 0}
- La courbe représentative d'une telle fonction est une parabole dont le sommet a pour coordonnées (0~; c) et admettant une symétrie par rapport à l'axe des ordonnées.
- Si a > 0, la fonction est strictement décroissante sur ]-\infty~; 0], puis strictement croissante sur [0 ~;+\infty[.
Si a \lt 0, la fonction est strictement croissante sur ]-\infty~; 0], puis strictement décroissante sur [0 ~;+\infty[.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Étudier des fonctions du type \boldsymbol{x \mapsto a\left(x-x_{1}\right)\left(x-x_{2}\right)} ou \boldsymbol{x \mapsto a\left(x-x_{1}\right)\left(x-x_{2}\right)\left(x-x_{3}\right)}, \boldsymbol{a \neq 0}
- Ces fonctions s'annulent uniquement en x_1 et en x_2 (et en x_3 pour la seconde). Ces réels sont les racines du polynôme.
- On étudie le signe de cette fonction à l'aide d'un tableau de signe dans lequel apparaît le signe de a, le signe de x-x_1 et le signe de x-x_2 (et le signe de x-x_3 pour la seconde fonction). On conclut à l'aide de la règle des signes.
- La courbe représentative de la fonction x \mapsto a\left(x-x_{1}\right)\left(x-x_{2}\right) est une parabole dont le sommet a pour abscisse \frac{x_{1}+x_{2}}{2}. Elle est symétrique par rapport à la droite verticale d'équation x=\frac{x_{1}+x_{2}}{2}.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Étudier des fonctions du type \boldsymbol{x \mapsto a x^{3}+d}, \boldsymbol{a \neq 0}
- Si a > 0, la fonction est strictement croissante sur \mathbb{R}. Si a \lt 0, la fonction est strictement décroissante sur \mathbb{R}.
- Pour tout réel \alpha, l'équation x^3 = \alpha admet une unique solution notée \sqrt[3]{\alpha} ou \alpha^{\normalsize{\tfrac{1}{3}}}.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
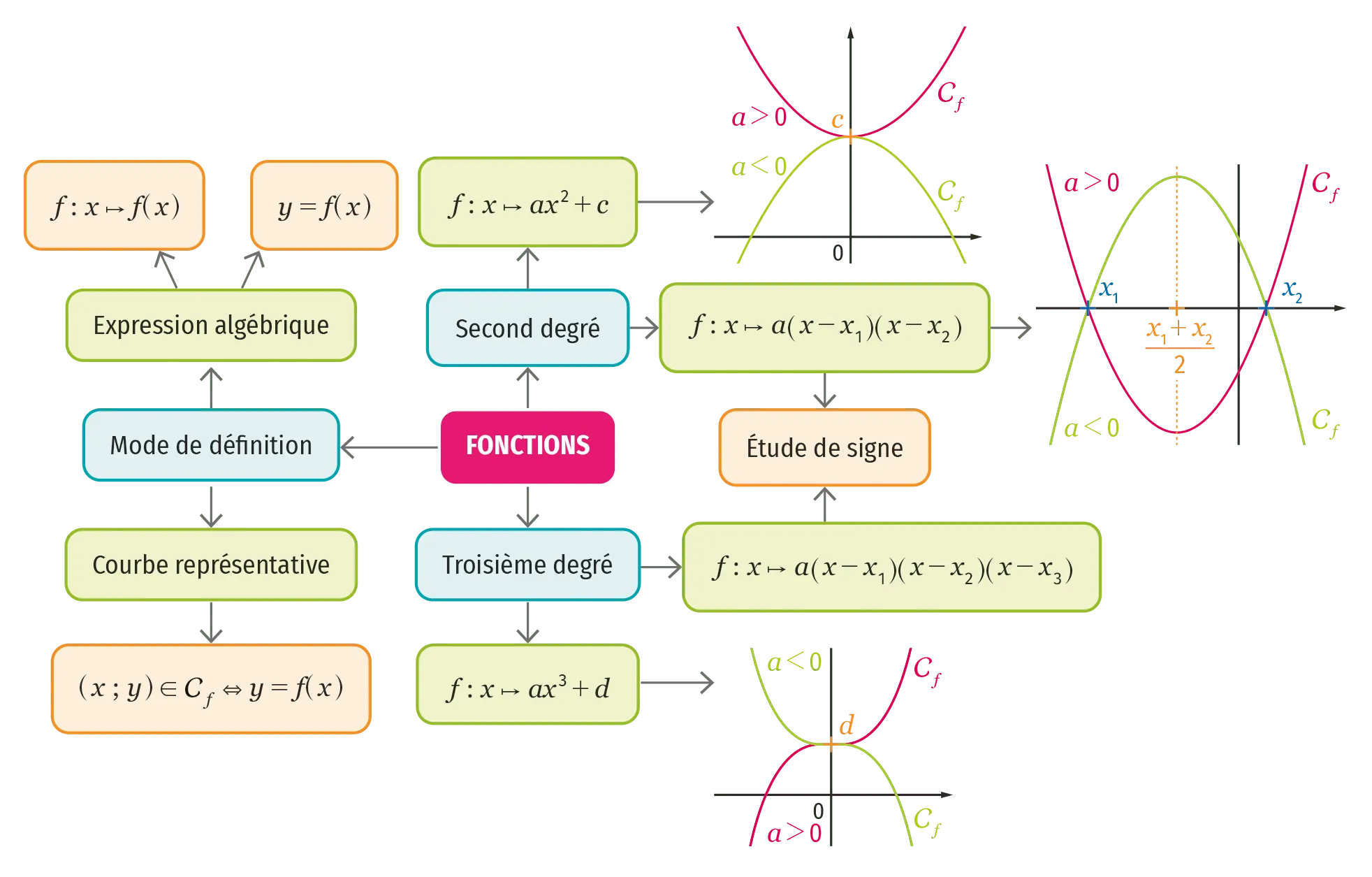
Carte mentale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
