Chapitre 11
Entraînement 1
Primitive d'une fonction sur un intervalle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 52
Vrai / Faux
[Raisonner.]
L'affirmation suivante est‑elle vraie ou fausse ? Justifier.
« La fonction \text{F} définie sur \R par \text{F}(x) = x^2 + 5x est une primitive de la fonction f définie sur \R par f(x) = x + 5. »
« La fonction \text{F} définie sur \R par \text{F}(x) = x^2 + 5x est une primitive de la fonction f définie sur \R par f(x) = x + 5. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 53
Vrai / Faux
[Raisonner.]
L'affirmation suivante est‑elle vraie ou fausse ? Justifier.
« Si \text{I} et \text{J} sont deux primitives d'une même fonction i sur un intervalle, alors il existe un réel k tel que \text{I} - \text{J} = k. »
« Si \text{I} et \text{J} sont deux primitives d'une même fonction i sur un intervalle, alors il existe un réel k tel que \text{I} - \text{J} = k. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 54
[Raisonner.]
Dans chaque cas, déterminer si la fonction \text{F} est une
primitive de la fonction f sur \R.
1. f(x)=23 et \mathrm{F}(x)=23 x.
2. f(x)=12 et \mathrm{F}(x)=12 x-189.
3. f(x)=24 x et \mathrm{F}(x)=24 x^{2}-18.
4. f(x)=-8 x et \mathrm{F}(x)=-4 x^{2}+2 x.
5. f(x)=\frac{3}{5} x et \mathrm{F}(x)=\frac{3}{10} x^{2}-28.
6. f(x)=-\frac{1}{2} x+2 et \mathrm{F}(x)=-x^{2}+2 x.
1. f(x)=23 et \mathrm{F}(x)=23 x.
2. f(x)=12 et \mathrm{F}(x)=12 x-189.
3. f(x)=24 x et \mathrm{F}(x)=24 x^{2}-18.
4. f(x)=-8 x et \mathrm{F}(x)=-4 x^{2}+2 x.
5. f(x)=\frac{3}{5} x et \mathrm{F}(x)=\frac{3}{10} x^{2}-28.
6. f(x)=-\frac{1}{2} x+2 et \mathrm{F}(x)=-x^{2}+2 x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 55
[Raisonner.]
Dans chaque cas, déterminer si la fonction \text{F} est une primitive de la fonction f sur \R.
1. f(x)=15 x+2 et \mathrm{F}(x)=15 x^{2}+2 x+1.
2. f(x)=x^{2}+3 x-7 et \mathrm{F}(x)=\frac{x^{3}}{3}+\frac{3 x^{2}}{2}-7 x+2.
3. f(x)=3 x+\cos (4 x+5) et \mathrm{F}(x)=\frac{3 x^{2}}{2}+\sin (4 x+5).
4. f(x)=\cos ^{2}(x)-\sin ^{2}(x) et \mathrm{F}(x)=\cos (x) \sin (x).
1. f(x)=15 x+2 et \mathrm{F}(x)=15 x^{2}+2 x+1.
2. f(x)=x^{2}+3 x-7 et \mathrm{F}(x)=\frac{x^{3}}{3}+\frac{3 x^{2}}{2}-7 x+2.
3. f(x)=3 x+\cos (4 x+5) et \mathrm{F}(x)=\frac{3 x^{2}}{2}+\sin (4 x+5).
4. f(x)=\cos ^{2}(x)-\sin ^{2}(x) et \mathrm{F}(x)=\cos (x) \sin (x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 56
Vrai / Faux
[Raisonner.]
Soient f et \text{F} deux fonctions définies sur un intervalle \text{I} de \R et k un réel.
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse en justifiant.
1. Si \mathrm{F}^{\prime}=f sur \text{I,} alors f est une primitive de \text{F} sur \text{I.}
2. Si \mathrm{F}^{\prime}=f sur \text{I,} alors \text{F} est une primitive de f sur \text{I.}
3. Si \text{F} est une primitive de f sur \text{I,} alors \text{F} + k est une primitive de f sur \text{I.}
4. Si \text{F} est une primitive de f sur \text{I,} alors \text{F} est croissante sur \text{I} si, et seulement si, f est positive sur \text{I.}
5. Si \text{F} est une primitive de f sur \text{I,} alors \text{F} est négative sur \text{I} si, et seulement si, f est décroissante sur \text{I.}
Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse en justifiant.
1. Si \mathrm{F}^{\prime}=f sur \text{I,} alors f est une primitive de \text{F} sur \text{I.}
2. Si \mathrm{F}^{\prime}=f sur \text{I,} alors \text{F} est une primitive de f sur \text{I.}
3. Si \text{F} est une primitive de f sur \text{I,} alors \text{F} + k est une primitive de f sur \text{I.}
4. Si \text{F} est une primitive de f sur \text{I,} alors \text{F} est croissante sur \text{I} si, et seulement si, f est positive sur \text{I.}
5. Si \text{F} est une primitive de f sur \text{I,} alors \text{F} est négative sur \text{I} si, et seulement si, f est décroissante sur \text{I.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 57
[Raisonner.]
Dans chaque cas, déterminer si la fonction \text{F} est une
primitive de la fonction f sur \R.
1. f(x)=x^{4}+8 x^{3}+\sin (3 x+2) et \mathrm{F}(x)=\frac{x^{5}}{5}+2 x^{4}-\frac{1}{3} \cos (3 x+2)-4.
2. f(x)=18 \sin (3 x+\pi)+5 \cos \left(6 x+\frac{\pi}{2}\right) et \mathrm{F}(x)=-6 \cos (3 x+\pi)+\frac{5}{6} \sin \left(6 x+\frac{\pi}{2}\right)+25 .
3. f(x)=4 \sin (9 x+\pi)+8 x^{6}+9 x-6 \cos (5 x-\pi) et \mathrm{F}(x)=\frac{-4}{9} \cos (9 x+\pi)+\frac{8 x^{7}}{7}+\frac{9 x^{2}}{2}-\frac{6}{5} \sin (5 x-\pi)-12.
4. f(x)=x\left(2 \cos (x)-x^{2} \sin (x)\right) et \mathrm{F}(x)=x^{2} \cos (x).
1. f(x)=x^{4}+8 x^{3}+\sin (3 x+2) et \mathrm{F}(x)=\frac{x^{5}}{5}+2 x^{4}-\frac{1}{3} \cos (3 x+2)-4.
2. f(x)=18 \sin (3 x+\pi)+5 \cos \left(6 x+\frac{\pi}{2}\right) et \mathrm{F}(x)=-6 \cos (3 x+\pi)+\frac{5}{6} \sin \left(6 x+\frac{\pi}{2}\right)+25 .
3. f(x)=4 \sin (9 x+\pi)+8 x^{6}+9 x-6 \cos (5 x-\pi) et \mathrm{F}(x)=\frac{-4}{9} \cos (9 x+\pi)+\frac{8 x^{7}}{7}+\frac{9 x^{2}}{2}-\frac{6}{5} \sin (5 x-\pi)-12.
4. f(x)=x\left(2 \cos (x)-x^{2} \sin (x)\right) et \mathrm{F}(x)=x^{2} \cos (x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 58
[Raisonner.]
Dans chaque cas, montrer que la fonction \text{F} est une primitive de la fonction f définie sur \R.
Déterminer ensuite l'ensemble des primitives de f sur \R.
1. f(x)=10 et \mathrm{F}(x)=10 x-3.
2. f(x)=-\frac{8}{11} et \mathrm{F}(x)=-\frac{8 x}{11}-7.
3. f(x)=2 x-2 et \mathrm{F}(x)=x^{2}-2 x+9.
Déterminer ensuite l'ensemble des primitives de f sur \R.
1. f(x)=10 et \mathrm{F}(x)=10 x-3.
2. f(x)=-\frac{8}{11} et \mathrm{F}(x)=-\frac{8 x}{11}-7.
3. f(x)=2 x-2 et \mathrm{F}(x)=x^{2}-2 x+9.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 59
[Raisonner.]
Dans chaque cas, montrer que la fonction \text{F} est une primitive de la fonction f définie sur \R.
Déterminer ensuite l'ensemble des primitives de f sur \R.
1. f(x)=\frac{1}{5} x^{2}+9 x-2 et \text{F}(x)=\frac{1}{15} x^{3}+\frac{9 x^{2}}{2}-2 x+11.
2. f(x)=\frac{3 x^{3}}{7}-10 x^{2}-\frac{4}{13} et \text{F}(x)=\frac{3 x^{4}}{28}-\frac{10 x^{3}}{3}-\frac{4 x}{13}+7.
3. f(x)=2 \sin (5 x+4) et \text{F}(x)=\frac{-2}{5} \cos (5 x+4).
Déterminer ensuite l'ensemble des primitives de f sur \R.
1. f(x)=\frac{1}{5} x^{2}+9 x-2 et \text{F}(x)=\frac{1}{15} x^{3}+\frac{9 x^{2}}{2}-2 x+11.
2. f(x)=\frac{3 x^{3}}{7}-10 x^{2}-\frac{4}{13} et \text{F}(x)=\frac{3 x^{4}}{28}-\frac{10 x^{3}}{3}-\frac{4 x}{13}+7.
3. f(x)=2 \sin (5 x+4) et \text{F}(x)=\frac{-2}{5} \cos (5 x+4).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 60
[Raisonner.]
Dans chaque cas, montrer que la fonction \text{F} est une primitive de f définie sur \R.
Déterminer l'ensemble des primitives de f sur \R.
1. f(x)=2 x+1 et \mathrm{F}(x)=(x+3)(x-2).
2. f(x)=\cos (4 x+9)-5 \sin \left(6 x+\frac{\pi}{2}\right) et \mathrm{F}(x)=\frac{1}{4} \sin (4 x+9)+\frac{5}{6} \cos \left(6 x+\frac{\pi}{2}\right)-15.
3. f(x)=\frac{x^{6}}{2}-\frac{6 x^{3}}{7}-\frac{8 x}{11}-4 \cos (3 x-8) et \mathrm{F}(x)=\frac{x^{7}}{14}-\frac{6 x^{4}}{28}-\frac{4 x^{2}}{11}-\frac{4}{3} \sin (3 x-8)+82.
Déterminer l'ensemble des primitives de f sur \R.
1. f(x)=2 x+1 et \mathrm{F}(x)=(x+3)(x-2).
2. f(x)=\cos (4 x+9)-5 \sin \left(6 x+\frac{\pi}{2}\right) et \mathrm{F}(x)=\frac{1}{4} \sin (4 x+9)+\frac{5}{6} \cos \left(6 x+\frac{\pi}{2}\right)-15.
3. f(x)=\frac{x^{6}}{2}-\frac{6 x^{3}}{7}-\frac{8 x}{11}-4 \cos (3 x-8) et \mathrm{F}(x)=\frac{x^{7}}{14}-\frac{6 x^{4}}{28}-\frac{4 x^{2}}{11}-\frac{4}{3} \sin (3 x-8)+82.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 61
[Raisonner.]
Dans chaque cas, vérifier que \text{F} est une primitive de la fonction f définie sur \text{I,} puis déterminer la primitive \text{F}_1 de f qui s'annule en x_0.
1. f(x)=5 et \mathrm{F}(x)=5 x+1 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
2. f(x)=-12 et \mathrm{F}(x)=-12 x-2 sur \mathrm{I}=\mathbb{R} avec x_{0}=-1.
3. f(x)=2 x et \mathrm{F}(x)=x^{2}+1 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
1. f(x)=5 et \mathrm{F}(x)=5 x+1 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
2. f(x)=-12 et \mathrm{F}(x)=-12 x-2 sur \mathrm{I}=\mathbb{R} avec x_{0}=-1.
3. f(x)=2 x et \mathrm{F}(x)=x^{2}+1 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 62
[Raisonner.]
Dans chaque cas, vérifier que \text{F} est une primitive de la fonction f définie sur \text{I,} puis déterminer la primitive \text{F}_1 de f qui s'annule en x_0.
1. f(x)=x+6 et \mathrm{F}(x)=\frac{x^{2}}{2}+6 x-2 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
2. f(x)=3 x-7 et \mathrm{F}(x)=\frac{3 x^{2}}{2}-7 x+3 sur \mathrm{I}=\mathbb{R} avec x_{0}=-1.
3. f(x)=3 x^{2}-7 et \mathrm{F}(x)=x^{3}-7 x+5 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
1. f(x)=x+6 et \mathrm{F}(x)=\frac{x^{2}}{2}+6 x-2 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
2. f(x)=3 x-7 et \mathrm{F}(x)=\frac{3 x^{2}}{2}-7 x+3 sur \mathrm{I}=\mathbb{R} avec x_{0}=-1.
3. f(x)=3 x^{2}-7 et \mathrm{F}(x)=x^{3}-7 x+5 sur \mathrm{I}=\mathbb{R} avec x_{0}=1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 63
[Raisonner.]
Dans chaque cas, vérifier que \text{F} est une primitive de la fonction f définie sur \text{I,} puis déterminer la primitive \text{F}_1 de f qui s'annule en x_0.
1. f(x)=4 \sin (x+\pi) et \mathrm{F}(x)=-4 \cos (x+\pi)-5 sur \mathrm{I}=\mathbb{R} avec x_{0}=\pi.
2. f(x)=\cos \left(2 x+\frac{\pi}{2}\right)-\sin (4 x+\pi) et \mathrm{F}(x)=\frac{1}{2} \sin \left(2 x+\frac{\pi}{2}\right)+\frac{1}{4} \cos (4 x+\pi)-1 sur \mathrm{I}=\mathbb{R} avec x_{0}=0.
3. f(x)=7 \cos (5 x+\pi)+\frac{5 x^{4}}{6}-9 x et \mathrm{F}(x)=\frac{7}{5} \sin (5 x+\pi)+\frac{x^{5}}{6}-\frac{9 x^{2}}{2} sur \mathrm{I}=\mathbb{R} avec x_{0}=0.
4. f(x)=\frac{10}{(x+2)^{2}} et \mathrm{F}(x)=\frac{3 x-4}{x+2} sur \mathrm{I}=[0 \:;+\infty[ avec x_{0}=0.
1. f(x)=4 \sin (x+\pi) et \mathrm{F}(x)=-4 \cos (x+\pi)-5 sur \mathrm{I}=\mathbb{R} avec x_{0}=\pi.
2. f(x)=\cos \left(2 x+\frac{\pi}{2}\right)-\sin (4 x+\pi) et \mathrm{F}(x)=\frac{1}{2} \sin \left(2 x+\frac{\pi}{2}\right)+\frac{1}{4} \cos (4 x+\pi)-1 sur \mathrm{I}=\mathbb{R} avec x_{0}=0.
3. f(x)=7 \cos (5 x+\pi)+\frac{5 x^{4}}{6}-9 x et \mathrm{F}(x)=\frac{7}{5} \sin (5 x+\pi)+\frac{x^{5}}{6}-\frac{9 x^{2}}{2} sur \mathrm{I}=\mathbb{R} avec x_{0}=0.
4. f(x)=\frac{10}{(x+2)^{2}} et \mathrm{F}(x)=\frac{3 x-4}{x+2} sur \mathrm{I}=[0 \:;+\infty[ avec x_{0}=0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 64
[Représenter.]
Parmi les fonctions g et h représentées ci‑dessous, quelle est celle qui correspond à une primitive de la fonction f ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 65
[Représenter.]
Soit f une fonction définie sur \R dont on donne
ci-dessous la représentation graphique \mathcal{C}_f.

À l'aide du graphique, déterminer les variations des primitives de f sur \R.

À l'aide du graphique, déterminer les variations des primitives de f sur \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 66
[Représenter.]
On a représenté deux fonctions f et g définies sur \R dans un repère du plan. Déterminer laquelle des deux est une primitive de l'autre.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 67
[Représenter.]
On donne la représentation graphique \mathcal{C}_f d'une fonction f définie sur l'intervalle \text{I} = [-3 \:; 2] dans un repère du plan.
Déterminer, en justifiant, les variations d'une primitive \text{F} de f sur \text{I.}


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 68
[Calculer.]
Lorsqu'on lui demande de déterminer une primitive de la fonction f définie sur \mathbb{R} par f(x)=\frac{3 x^{4}}{2}+3 x+7, un logiciel de calcul formel donne le résultat suivant.

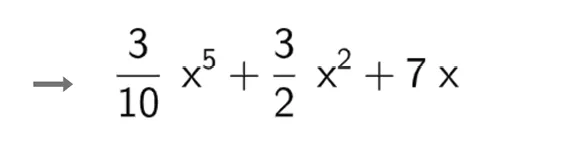
1. Vérifier le résultat obtenu.
2. En déduire la primitive \text{F}_1 de f vérifiant \text{F}_1(1) = 1.

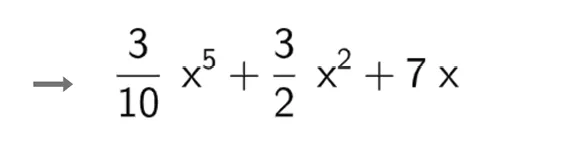
1. Vérifier le résultat obtenu.
2. En déduire la primitive \text{F}_1 de f vérifiant \text{F}_1(1) = 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 69
Démo
[Raisonner.]
Soient \text{F} une primitive d'une fonction f définie sur un intervalle \text{I} et \text{G} la fonction définie sur \text{I} par \text{G}(x) = \text{F}(x) + k, où k désigne un réel.
1. Montrer que \text{G} est aussi une primitive de f sur \text{I.}
2. Soit \text{H} une autre primitive de f sur \text{I.} Que vaut (\mathrm{F}-\mathrm{H})^{\prime} ? En déduire que \mathrm{F}-\mathrm{H} est une fonction constante, puis conclure.
1. Montrer que \text{G} est aussi une primitive de f sur \text{I.}
2. Soit \text{H} une autre primitive de f sur \text{I.} Que vaut (\mathrm{F}-\mathrm{H})^{\prime} ? En déduire que \mathrm{F}-\mathrm{H} est une fonction constante, puis conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 70
[Raisonner.]


Un TGV part de la gare à l'instant t = 0 s avec une accélération constante a = 0{,}15 m/s2 et sans vitesse initiale.
1. Montrer que, pour tout t \in [0 \:; 2\:500], la vitesse v(t), en m/s, est égale à v(t) = 0{,}15t.
2. Déterminer l'expression, en fonction de t, de la distance x(t), en mètre, parcourue par le TGV à l'instant t. On supposera que x(0) = 0.
3. Lors de son accélération, combien de temps le TGV aura‑t‑il mis pour parcourir les douze premiers kilomètres ?
Histoire des maths
Le 20 janvier 1700, le mathématicien Pierre Varignon a formalisé la notion d'accélération comme un écart infiniment petit de vitesse \text{d}v pendant un temps infiniment petit \text{d}t.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 71
[Raisonner.]
Un solide (S) est accroché à un ressort (R) sur un axe horizontal. Il effectue des oscillations si on l'écarte de sa position d'équilibre.

À l'instant t, mesuré en seconde dans [0 \:; 300], la position du solide dans le repère (\mathrm{O} \:; \vec{i}), en mètre, est donnée par : x(t)=\frac{\sqrt{3}}{2} \cos \left(4 t-\frac{\pi}{2}\right).
Sa vitesse à l'instant t est donnée par : v(t)=-2 \sqrt{3} \sin \left(4 t-\frac{\pi}{2}\right).
Vérifier sur cet exemple, que x est bien la primitive de v vérifiant x(0) = 0.

À l'instant t, mesuré en seconde dans [0 \:; 300], la position du solide dans le repère (\mathrm{O} \:; \vec{i}), en mètre, est donnée par : x(t)=\frac{\sqrt{3}}{2} \cos \left(4 t-\frac{\pi}{2}\right).
Sa vitesse à l'instant t est donnée par : v(t)=-2 \sqrt{3} \sin \left(4 t-\frac{\pi}{2}\right).
Vérifier sur cet exemple, que x est bien la primitive de v vérifiant x(0) = 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 72
Exercice inversé
En réponse à un exercice, on écrit : « Donc les fonctions \text{F} et \text{G} sont des primitives de f sur \R. » Rédiger un énoncé possible de cet exercice.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 73
Exercice inversé
Rédiger un énoncé dont la réponse est :
« La primitive \text{F} recherchée est définie sur \R par \text{F}(x) = 7x^3 - \frac{6}{5} x^{2} - 3x + 4 ».
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

