Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 11
L'essentiel
Primitives
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiche méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Vérifier que \mathbf{F} est une primitive d'une fonction \boldsymbol{f} sur un intervalle \mathbf{I}
- On calcule la dérivée \text{F}^{\prime} de \text{F} et on la compare à f : si \text{F}^{\prime} = f, alors \text{F} est une primitive de f sur \text{I.}
Auto-évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Déterminer une primitive \mathbf{F} d'une fonction \boldsymbol{f} sur \mathbf{I}
- On utilise le tableau des primitives des fonctions de référence en identifiant le type de fonction de référence.
- Si la fonction f est égale à la somme de plusieurs fonctions de référence, alors une primitive \text{F} de f est égale à la somme des primitives de ces fonctions de référence.
- Si la fonction f est égale au produit d'une fonction de référence par une constante réelle, alors une primitive \text{F} de f est égale au produit de la primitive de cette fonction de référence par la constante.
Auto-évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Déterminer toutes les primitives de \boldsymbol{f} sur \mathbf{I}
- On détermine une primitive \text{F} de f sur \text{I.}
- Les autres primitives de f sont de la forme \text{F} + k, où k \in \R.
Auto-évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Déterminer la primitive \mathbf{F} d'une fonction \boldsymbol{f} vérifiant une condition du type \mathbf{F}\left(\boldsymbol{x}_\boldsymbol{0}\right)=\boldsymbol{y}_\boldsymbol{0}
- On détermine l'ensemble des primitives de f sur \text{I.}
- On écrit l'égalité \text{F}(x_0) = y_0 et on trouve k à l'aide de cette égalité (résolution d'équation).
Auto-évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
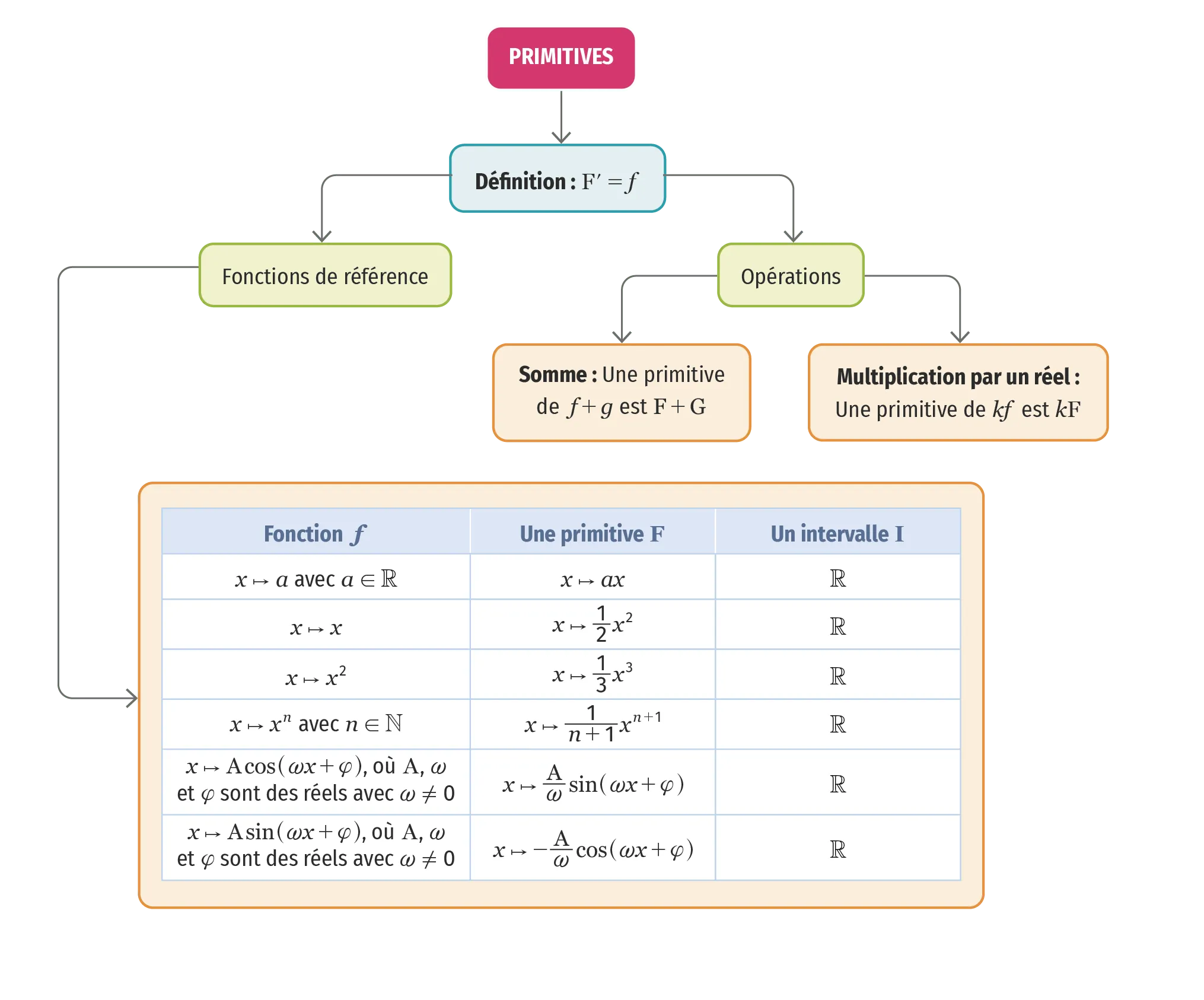
Carte mentale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah