Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 3
L'essentiel
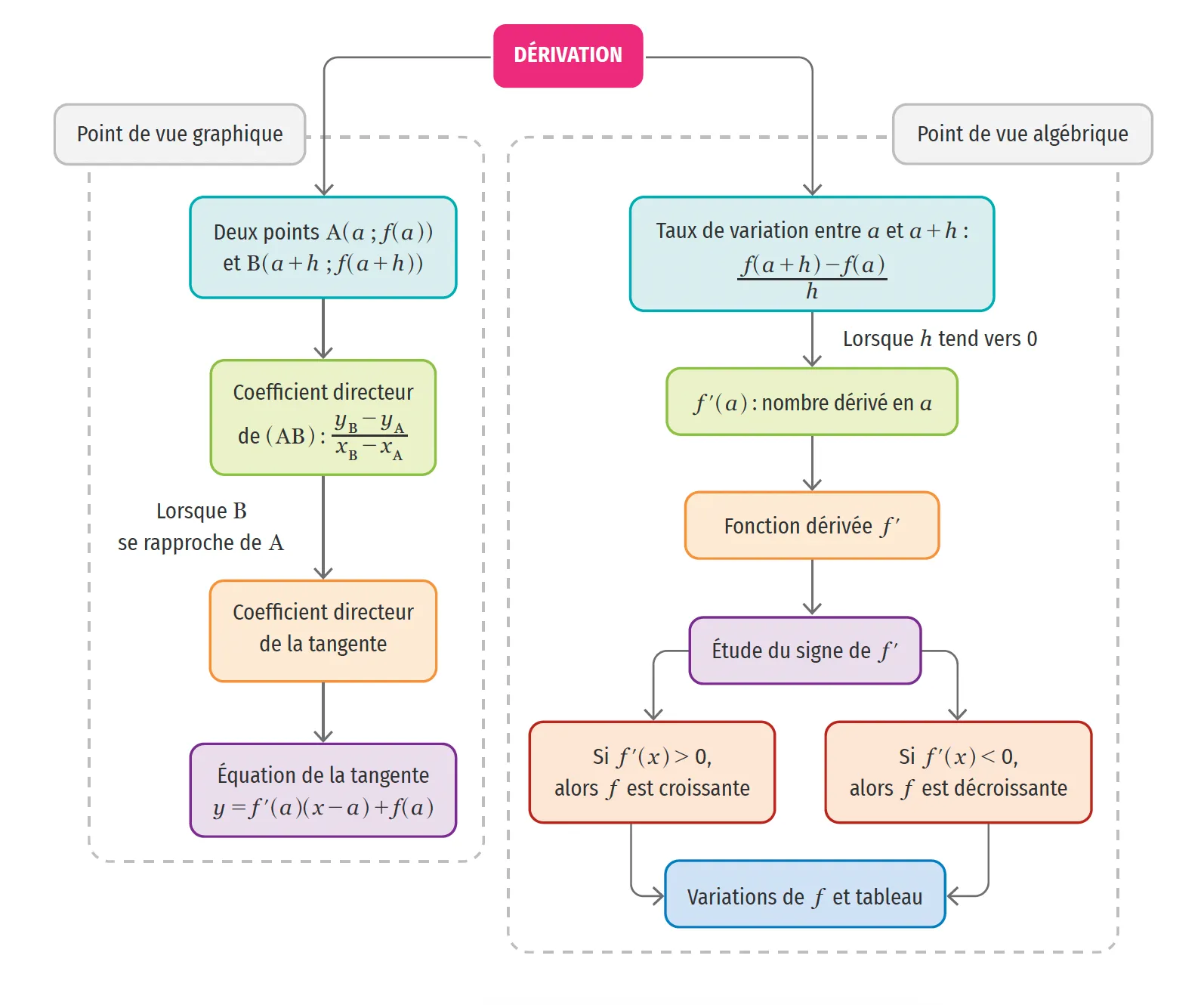
Dérivation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiche méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Calculer un taux de variation
- On cherche les valeurs a, a+h (ou b) et leurs images par f.
- On applique la formule \tau=\frac{f(a+h)-f(a)}{h} ou \tau=\frac{f(b)-f(a)}{b-a}.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Déterminer graphiquement un nombre dérivé
- On repère la tangente à la courbe représentative de la fonction au point d'abscisse a.
- On calcule le coefficient directeur de cette tangente.
- La valeur obtenue est f^{\prime}(a).
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Déterminer une équation réduite de tangente
- On repère l'abscisse a et son image f(a).
- On calcule (ou on lit) la valeur de f^{\prime}(a) (voir éventuellement le point précédent).
- On remplace ces valeurs dans la formule y=f^{\prime}(a)(x-a)+f(a) (et on développe éventuellement l'expression jusqu'à obtenir une équation de droite de la forme y = mx + p).
Auto‑évaluation ;
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Étudier les variations d'une fonction f
- On détermine la fonction dérivée f^{\prime} de la fonction f étudiée.
- On étudie le signe de f^{\prime} (éventuellement en construisant un tableau de signe).
- Si f^{\prime} est négative, alors la fonction est décroissante. Si f^{\prime} est positive, alors la fonction est croissante.
Auto‑évaluation ;
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Carte mentale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah