Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 3
Exercices
Synthèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 87 [Calculer, Modéliser.]
D'après bac ST2S, Polynésie, 2019
Partie A
On considère la fonction f définie sur l'intervalle [0 \: ; 15] par f(x)=x^{3}-21 x^{2}+120 x+50.
On note f^{\prime} la fonction dérivée de f sur cet intervalle.
1. Calculer f(4) et f(10).
2. a. Déterminer, pour tout x \in[0 \: ; 15], une expression de f^{\prime}(x).
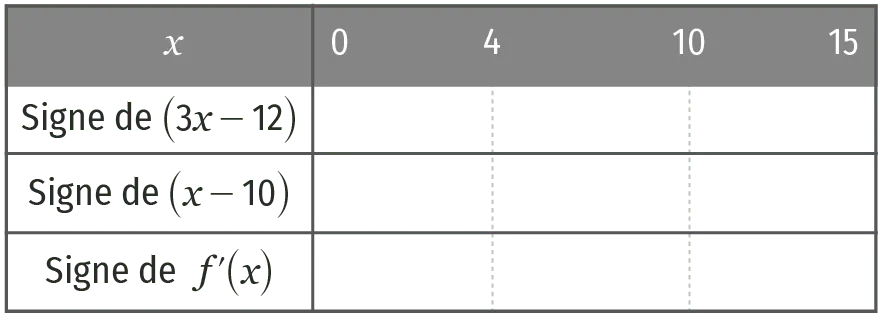
b. Vérifier que, pour tout réel x de l'intervalle [0 \: ; 15], on a f^{\prime}(x)=(3 x-12)(x-10).
3. Étudier le signe de f^{\prime}(x) sur l'intervalle [0 \: ; 15]. Pour ce faire, compléter le tableau de signe suivant grâce à notre outil de retouche image.
4. En déduire les variations de la fonction f sur [0 \: ; 15].
Partie B
Des analyses ont montré que des microalgues étaient naturellement présentes dans l'eau de mer avec une concentration normale comprise entre 0 et 100 milligrammes par litre (mg/L).
Ces microalgues ont tendance à se multiplier lorsque la salinité de l'eau de mer diminue.
Les autorités sanitaires considèrent qu'elles deviennent dangereuses pour la santé lorsque leur concentration dépasse 200 mg/L. Il faut alors prendre des mesures comme l'interdiction de la baignade.
La courbe donnée ci‑dessous modélise l'évolution de la concentration en microalgues de l'eau de baignade d'une plage du littoral pendant les dix jours qui ont suivi un très fort orage. Il s'agit de la courbe de la fonction f étudiée dans la partie A mais dont l'ensemble de définition est, dans cette partie B, restreint à l'intervalle [0 \: ; 10].
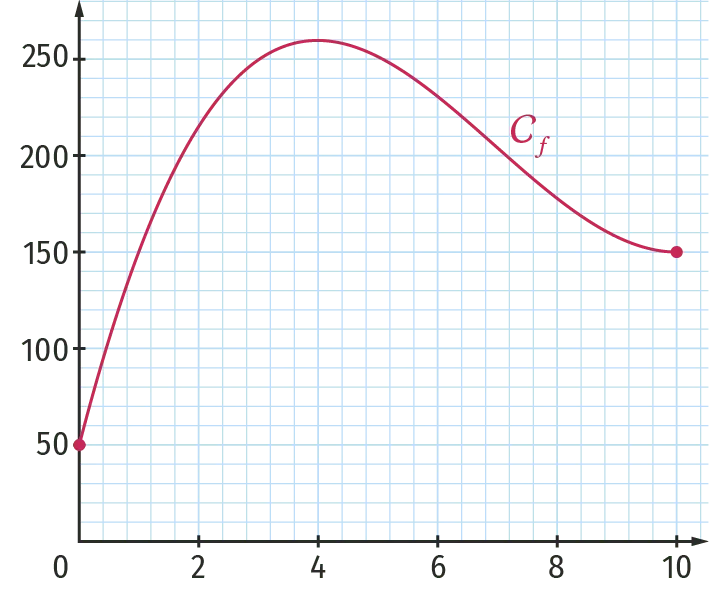
1. Pendant combien de jours complets la baignade est‑elle interdite ?
2. Quelle est la concentration maximale en microalgues durant les dix jours suivant l'orage ? Au bout de combien de jours a‑t‑elle été atteinte ?
3. Peut‑on considérer que dix jours après l'orage, la situation est revenue à la normale ?
Partie A
On considère la fonction f définie sur l'intervalle [0 \: ; 15] par f(x)=x^{3}-21 x^{2}+120 x+50.
On note f^{\prime} la fonction dérivée de f sur cet intervalle.
1. Calculer f(4) et f(10).
2. a. Déterminer, pour tout x \in[0 \: ; 15], une expression de f^{\prime}(x).
b. Vérifier que, pour tout réel x de l'intervalle [0 \: ; 15], on a f^{\prime}(x)=(3 x-12)(x-10).
3. Étudier le signe de f^{\prime}(x) sur l'intervalle [0 \: ; 15]. Pour ce faire, compléter le tableau de signe suivant grâce à notre outil de retouche image.
4. En déduire les variations de la fonction f sur [0 \: ; 15].
Partie B
Des analyses ont montré que des microalgues étaient naturellement présentes dans l'eau de mer avec une concentration normale comprise entre 0 et 100 milligrammes par litre (mg/L).
Ces microalgues ont tendance à se multiplier lorsque la salinité de l'eau de mer diminue.
Les autorités sanitaires considèrent qu'elles deviennent dangereuses pour la santé lorsque leur concentration dépasse 200 mg/L. Il faut alors prendre des mesures comme l'interdiction de la baignade.
La courbe donnée ci‑dessous modélise l'évolution de la concentration en microalgues de l'eau de baignade d'une plage du littoral pendant les dix jours qui ont suivi un très fort orage. Il s'agit de la courbe de la fonction f étudiée dans la partie A mais dont l'ensemble de définition est, dans cette partie B, restreint à l'intervalle [0 \: ; 10].
1. Pendant combien de jours complets la baignade est‑elle interdite ?
2. Quelle est la concentration maximale en microalgues durant les dix jours suivant l'orage ? Au bout de combien de jours a‑t‑elle été atteinte ?
3. Peut‑on considérer que dix jours après l'orage, la situation est revenue à la normale ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 88 [Communiquer, Représenter.]
Dosage acide base
On souhaite doser une solution d'acide chlorhydrique par une solution d'hydroxyde de sodium (soude).
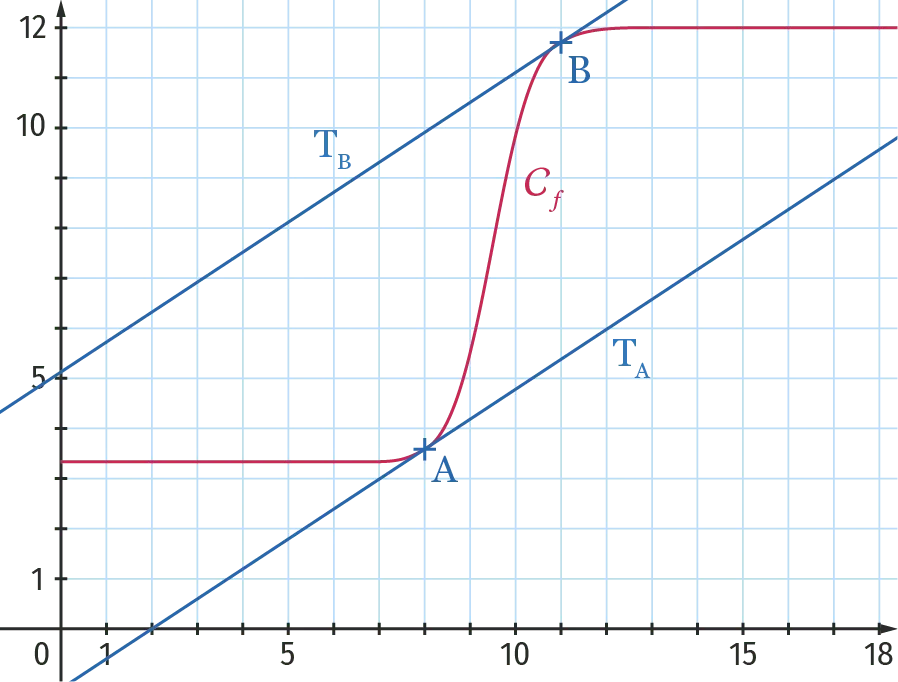
On construit la courbe ci‑dessous, mesurant le pH de la solution en fonction de la quantité (en mL) de soude ajoutée.
La tangente à cette courbe au point \mathrm{A}(8 \: ; 3{,}6) qu'on appelle \mathrm{T}_{\mathrm{A}}, coupe l'axe des abscisses en 2.
La tangente à la courbe en \mathrm{B}(11 \: ; 11{,}8), qu'on appelle \mathrm{T}_{\mathrm{B}}, coupe l'axe des ordonnées en 5{,}2.
1. Quel est le pH de la solution d'acide chlorhydrique avant l'ajout de soude ?
2. Établir une équation des droites \mathrm{T}_{\mathrm{A}} et \mathrm{T}_{\mathrm{B}}.
3. À quelle vitesse le pH augmente‑t‑il (en unité/mL ajouté) lorsqu'on a versé 8 mL de soude dans la solution ? Cette vitesse va‑t‑elle augmenter ou diminuer si on ajoute de la soude ?
4. Même question lorsqu'on a versé 1 mL de soude.
5. Estimer la quantité de soude à verser pour neutraliser la solution, c'est‑à‑dire pour obtenir \text{pH} = 7.
6. Commenter la vitesse de croissance du pH à cet instant.
On souhaite doser une solution d'acide chlorhydrique par une solution d'hydroxyde de sodium (soude).
On construit la courbe ci‑dessous, mesurant le pH de la solution en fonction de la quantité (en mL) de soude ajoutée.
La tangente à cette courbe au point \mathrm{A}(8 \: ; 3{,}6) qu'on appelle \mathrm{T}_{\mathrm{A}}, coupe l'axe des abscisses en 2.
La tangente à la courbe en \mathrm{B}(11 \: ; 11{,}8), qu'on appelle \mathrm{T}_{\mathrm{B}}, coupe l'axe des ordonnées en 5{,}2.
1. Quel est le pH de la solution d'acide chlorhydrique avant l'ajout de soude ?
2. Établir une équation des droites \mathrm{T}_{\mathrm{A}} et \mathrm{T}_{\mathrm{B}}.
3. À quelle vitesse le pH augmente‑t‑il (en unité/mL ajouté) lorsqu'on a versé 8 mL de soude dans la solution ? Cette vitesse va‑t‑elle augmenter ou diminuer si on ajoute de la soude ?
4. Même question lorsqu'on a versé 1 mL de soude.
5. Estimer la quantité de soude à verser pour neutraliser la solution, c'est‑à‑dire pour obtenir \text{pH} = 7.
6. Commenter la vitesse de croissance du pH à cet instant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 89 [Communiquer, Représenter.]
D'après bac ST2S, Polynésie, 2013
On a mesuré expérimentalement, sur une durée fixée, le taux d'évolution \text{P} du nombre de bactéries d'un type donné présentes dans un milieu à différentes températures. La courbe ci‑dessous modélise ce taux \text{P}, en pourcentage, en fonction de la température \text{T}, en degré Celsius, pour des valeurs comprises entre {-5} °C et {43} °C.
On suppose que \text{P} est dérivable.
1. Étudier graphiquement le signe de \mathrm{P}^{\prime}(\mathrm{T}) sur l'intervalle [-5 \: ; 43].
2. a. En déduire que la fonction \text{P} admet un maximum sur l'intervalle [-5 \: ; 43].
b. Pour quelle température le taux d'évolution de ce type de bactéries est‑il maximal ?
3. Estimer la température à laquelle l'augmentation du taux d'évolution de bactéries est la plus rapide.
4. a. Résoudre graphiquement l'équation \mathrm{P}(\mathrm{T})=0 sur l'intervalle [-5 \: ; 43].
b. Quelle interprétation peut‑on faire de la solution obtenue dans le contexte du développement de ce type de bactéries ?
On a mesuré expérimentalement, sur une durée fixée, le taux d'évolution \text{P} du nombre de bactéries d'un type donné présentes dans un milieu à différentes températures. La courbe ci‑dessous modélise ce taux \text{P}, en pourcentage, en fonction de la température \text{T}, en degré Celsius, pour des valeurs comprises entre {-5} °C et {43} °C.
On suppose que \text{P} est dérivable.
1. Étudier graphiquement le signe de \mathrm{P}^{\prime}(\mathrm{T}) sur l'intervalle [-5 \: ; 43].
2. a. En déduire que la fonction \text{P} admet un maximum sur l'intervalle [-5 \: ; 43].
b. Pour quelle température le taux d'évolution de ce type de bactéries est‑il maximal ?
3. Estimer la température à laquelle l'augmentation du taux d'évolution de bactéries est la plus rapide.
4. a. Résoudre graphiquement l'équation \mathrm{P}(\mathrm{T})=0 sur l'intervalle [-5 \: ; 43].
b. Quelle interprétation peut‑on faire de la solution obtenue dans le contexte du développement de ce type de bactéries ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 90 [Représenter, Modéliser.]
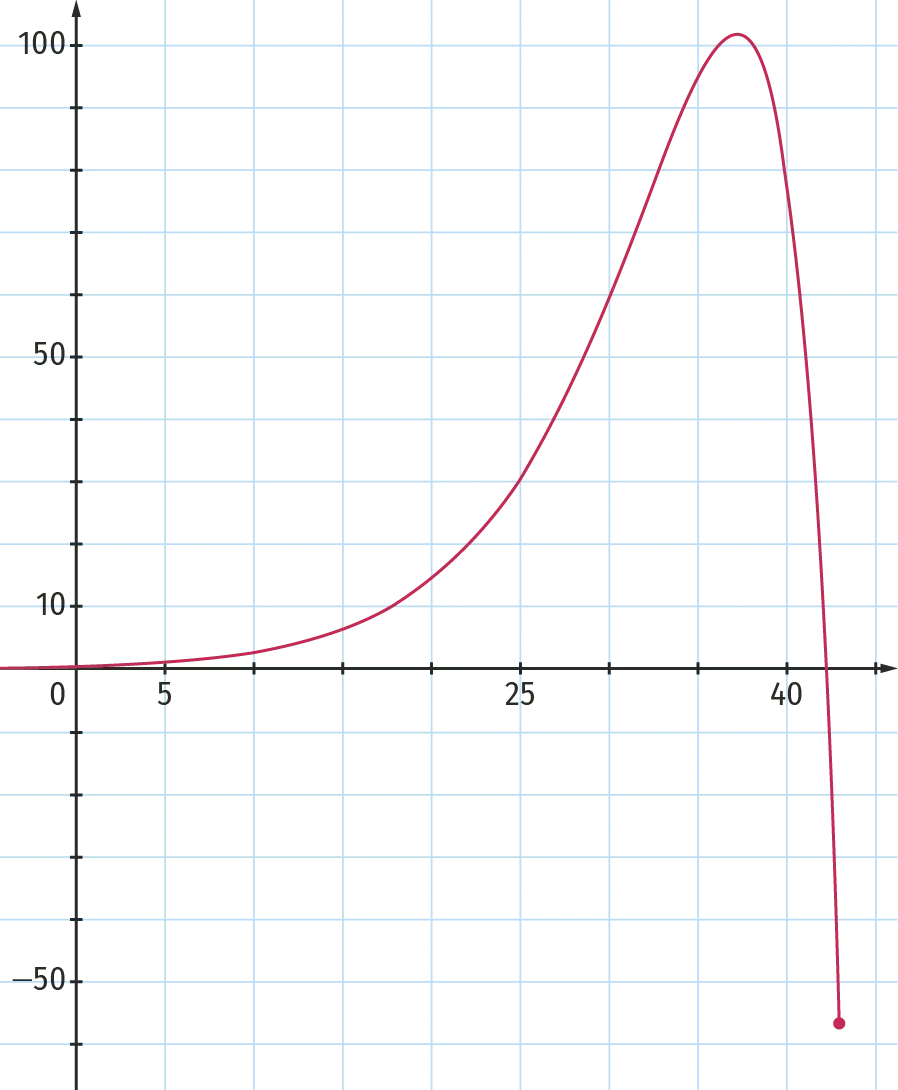
La courbe ci‑dessous représente une fonction f qui modélise la décharge suivie de la charge, en volts, d'un condensateur soumis à une tension de 2 V en fonction du temps t compris entre 0 et 10 secondes.
On a représenté la tangente \mathrm{T}_{\mathrm{A}} à la courbe au point \text{A} d'abscisse 1 et la tangente \mathrm{T}_{\mathrm{B}} au point \text{B} d'abscisse 6. \mathrm{T}_{\mathrm{A}} coupe l'axe des abscisses en 3 et \mathrm{T}_{\mathrm{B}} coupe l'axe des abscisses en 4{,}43.
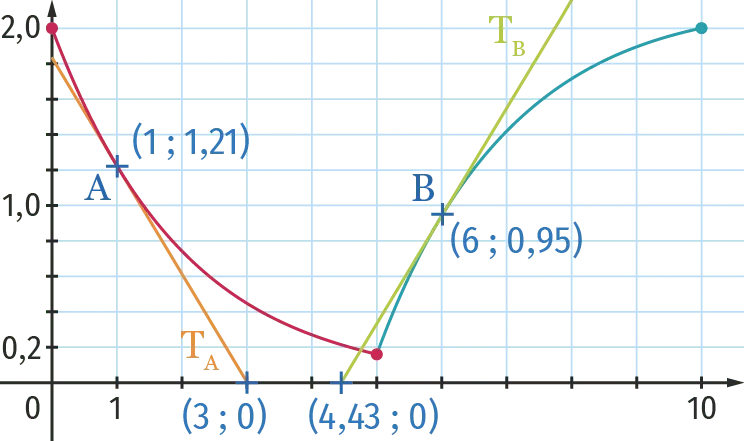
1. Expliquer pourquoi f(0)=2.
2. Par lecture graphique, déterminer l'intervalle de temps au cours duquel la tension dans le condensateur est inférieure à 1 V.
3. La vitesse de décharge est‑elle constante ? Croissante ? Décroissante ? Justifier.
4. Démontrer que f^{\prime}(1) \approx-f^{\prime}(6). Interpréter ce résultat en termes de vitesse de charge.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 91 [Modéliser, Calculer.]
On modélise le taux de remplissage, en %, d'un établissement touristique par une fonction f définie, pour tout x \in[1 \: ; 12], par f(x)=-\frac{13}{64} x^{3}+\frac{27}{16} x^{2}+12 x, où x correspond au numéro calendaire du mois (1 pour janvier, etc.).
1. Estimer le taux de remplissage de l'établissement aux mois de mai et d'octobre.
2. En traçant la courbe de f sur une calculatrice, estimer sur quelle période l'établissement touristique est rempli à plus de 75 %.
3. a. Calculer, pour tout x \in[1 \: ; 12], f^{\prime}(x).
b. Montrer que 8 est une racine du polynôme f^{\prime} et en déduire le tableau de signe de f^{\prime}(x) sur l'intervalle [1 \: ; 12].
c.
Construire le tableau de variations de f sur l'intervalle [1 \: ; 12]. Quel est le taux de remplissage maximum ?
1. Estimer le taux de remplissage de l'établissement aux mois de mai et d'octobre.
2. En traçant la courbe de f sur une calculatrice, estimer sur quelle période l'établissement touristique est rempli à plus de 75 %.
3. a. Calculer, pour tout x \in[1 \: ; 12], f^{\prime}(x).
b. Montrer que 8 est une racine du polynôme f^{\prime} et en déduire le tableau de signe de f^{\prime}(x) sur l'intervalle [1 \: ; 12].
Aide
On admettra que la seconde racine de f^{\prime} est négative.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 92 [Chercher, Calculer.]
Une entreprise fabrique et vend des smartphones. Le coût de production unitaire d'un smartphone, exprimé en euro, est modélisé par la fonction f définie, pour tout x \in[0 \: ; 160], par f(x)=-0{,}000\:1 x^{3}+0{,}033 x^{2}-3{,}63 x+190, où x est exprimé en millier de produits fabriqués et vendus. La courbe représentative de f est tracée dans le repère ci‑dessous.
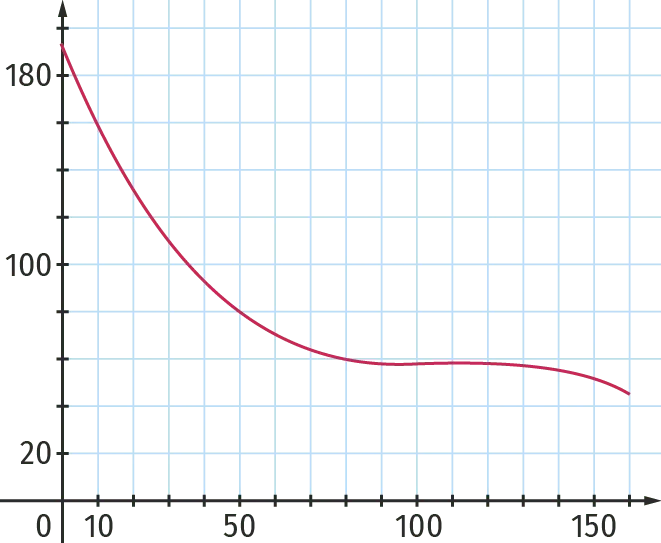
1. Déterminer le coût fixe de production, c'est‑à‑dire le coût de production pour 0 appareil fabriqué et vendu.
2. a. Calculer le coût unitaire de production de 20 000 smartphones.
b. Quel sera alors le coût total de production ?
3. a. On note f^{\prime} la fonction dérivée de f. Calculer f^{\prime}(x) pour tout réel x de l'intervalle [0 \: ; 160].
b. Démontrer que, pour tout x \in[0 \: ; 160], f^{\prime}(x)=-0,000\:3(x-110)^{2}, puis étudier le signe de f^{\prime}(x) pour x \in[0 \: ; 160].
c. En déduire le tableau de variations de f sur [0 \: ; 160].
4. a. Montrer que f^{\prime} s'annule en x = 110. La fonction f admet‑elle pour autant un extremum local en cette valeur ? Pourquoi ?
b. Le point d'abscisse 110 est appelé point d'inflexion de la courbe représentative de f. Pour quelle raison d'ordre économique peut‑on observer ce point d'inflexion dans le coût unitaire de production de ces produits ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 93 [Modéliser, Communiquer.]
Lors de l'interaction gravitationnelle entre deux corps séparés d'une distance r, on peut étudier une énergie appelée énergie potentielle effective, notée \mathrm{E}_{peff}, qui s'exprime en fonction de r.
Lors d'une expérience, on a représenté cette énergie, en joule, pour des valeurs de r entre 0 et 6 unités de longueur.
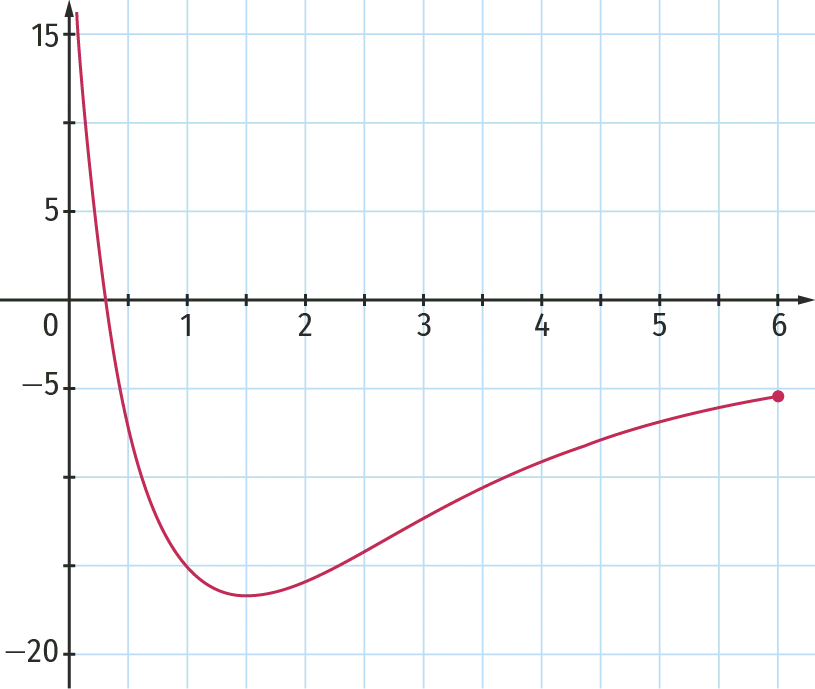
On note \mathrm{E}^{\prime} la fonction dérivée de cette fonction, représentée par le graphe ci‑dessous.
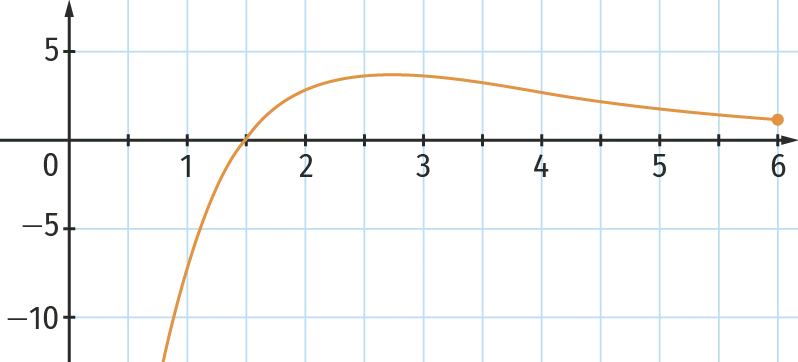
1. Graphiquement, donner une valeur approchée r_0, solution de l'équation \mathrm{E}^{\prime}(r)=0. Que peut‑on en déduire quant à l'énergie potentielle effective de l'expérience pour cette valeur ?
2. Graphiquement, pour quelle valeur r_{\text{max}} \: \mathrm{E}^{\prime}(r) atteint‑elle une valeur maximale ? Comment interpréter cette valeur maximale dans le graphique de l'énergie potentielle effective ?
3. Commenter l'évolution de l'énergie potentielle effective pour les cas suivants.
a. r \in\left[0 \: ; r_{0}\right]
b. r \in\left[r_{0} \: ; r_{\max }\right]
c. r \in\left[r_{\max} \: ; 10\right]
Lors d'une expérience, on a représenté cette énergie, en joule, pour des valeurs de r entre 0 et 6 unités de longueur.
On note \mathrm{E}^{\prime} la fonction dérivée de cette fonction, représentée par le graphe ci‑dessous.
1. Graphiquement, donner une valeur approchée r_0, solution de l'équation \mathrm{E}^{\prime}(r)=0. Que peut‑on en déduire quant à l'énergie potentielle effective de l'expérience pour cette valeur ?
2. Graphiquement, pour quelle valeur r_{\text{max}} \: \mathrm{E}^{\prime}(r) atteint‑elle une valeur maximale ? Comment interpréter cette valeur maximale dans le graphique de l'énergie potentielle effective ?
3. Commenter l'évolution de l'énergie potentielle effective pour les cas suivants.
a. r \in\left[0 \: ; r_{0}\right]
b. r \in\left[r_{0} \: ; r_{\max }\right]
c. r \in\left[r_{\max} \: ; 10\right]
Remarque
Si l'énergie potentielle effective est une notion difficile à interpréter, elle est couramment utilisée pour déterminer le mouvement d'un point matériel \text{M} soumis à une seule force centrale, c'est‑à‑dire une force toujours dirigée vers un même point.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 94 [Calculer, Représenter.]
D'après bac STMG, Polynésie, 2019
Une entreprise fabrique chaque jour des rouleaux de tissu en coton. La production quotidienne varie entre 1 et 10 kilomètres de tissu. On note x la production de tissu en kilomètres. Le coût net total de production, exprimé en euros, de x kilomètres de tissu est donné par la fonction \text{C} définie, pour x appartenant à [1 \: ; 10], par :
Partie A : Lecture graphique
On appelle coût moyen de production la fonction \mathrm{C}_{\mathrm{M}} définie sur l'intervalle [1 \: ; 10] par \mathrm{C}_{\mathrm{M}}(x)=\frac{\mathrm{C}(x)}{x}.
La représentation graphique de la fonction \mathrm{C}_{\mathrm{M}} est donnée ci‑dessous.
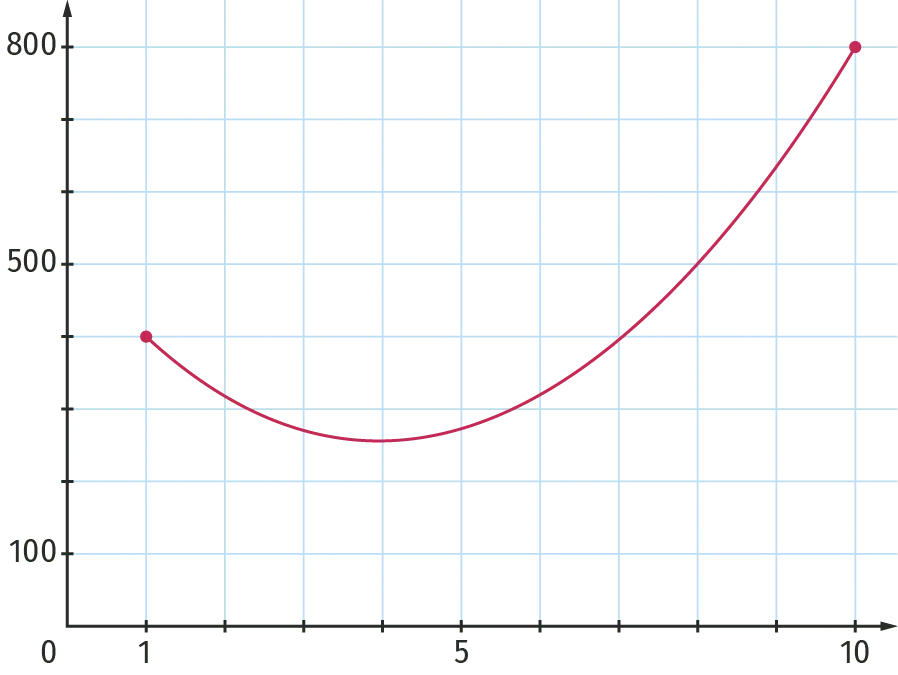
1. Donner par lecture graphique une valeur approchée de \mathrm{C}_{\mathrm{M}}(7).
2. À l'aide de la représentation graphique, dresser le tableau de variations de \mathrm{C}_{\mathrm{M}} sur [1 \: ; 10].
3. En déduire la longueur de tissu, en kilomètres, que l'entreprise doit fabriquer pour que le coût moyen de production soit minimal.
Partie B : Étude du bénéfice
On suppose que l'entreprise écoule systématiquement sa production journalière.
Le prix de vente d'un kilomètre de tissu est de 680 €.
On note \text{R}(x) la recette, exprimée en euros, correspondant à la vente de x kilomètres de tissu. On note \mathrm{B}(x) le bénéfice, exprimé en euro, réalisé par l'entreprise pour la vente de x kilomètres de tissu.
1. Exprimer \mathrm{R}(x) en fonction de x.
2. Justifier que l'expression de \mathrm{B}(x) en fonction de x est \text{B}(x)=-15 x^{3}+120 x^{2}+180 x
3. Pour tout nombre réel x appartenant à l'intervalle [1 \: ; 10], déterminer \mathrm{B}^{\prime}(x).
4. a. Montrer que, pour tout x \in[1 \: ; 10] \: :
b. En déduire le signe de la fonction \text{B}^{\prime} sur l'intervalle [1 \: ; 10] en s'aidant du tableau de signe suivant.
5. En utilisant la question précédente, construire le tableau de variations de la fonction \text{B} sur l'intervalle [1 \: ; 10].
6. Déterminer la longueur de tissu que l'entreprise doit produire et vendre chaque jour pour que le bénéfice réalisé soit maximal. Que vaut ce bénéfice maximal ?
Une entreprise fabrique chaque jour des rouleaux de tissu en coton. La production quotidienne varie entre 1 et 10 kilomètres de tissu. On note x la production de tissu en kilomètres. Le coût net total de production, exprimé en euros, de x kilomètres de tissu est donné par la fonction \text{C} définie, pour x appartenant à [1 \: ; 10], par :
\mathrm{C}(x)=15 x^{3}-120 x^{2}+500 x.
Partie A : Lecture graphique
On appelle coût moyen de production la fonction \mathrm{C}_{\mathrm{M}} définie sur l'intervalle [1 \: ; 10] par \mathrm{C}_{\mathrm{M}}(x)=\frac{\mathrm{C}(x)}{x}.
La représentation graphique de la fonction \mathrm{C}_{\mathrm{M}} est donnée ci‑dessous.
1. Donner par lecture graphique une valeur approchée de \mathrm{C}_{\mathrm{M}}(7).
2. À l'aide de la représentation graphique, dresser le tableau de variations de \mathrm{C}_{\mathrm{M}} sur [1 \: ; 10].
3. En déduire la longueur de tissu, en kilomètres, que l'entreprise doit fabriquer pour que le coût moyen de production soit minimal.
Partie B : Étude du bénéfice
On suppose que l'entreprise écoule systématiquement sa production journalière.
Le prix de vente d'un kilomètre de tissu est de 680 €.
On note \text{R}(x) la recette, exprimée en euros, correspondant à la vente de x kilomètres de tissu. On note \mathrm{B}(x) le bénéfice, exprimé en euro, réalisé par l'entreprise pour la vente de x kilomètres de tissu.
1. Exprimer \mathrm{R}(x) en fonction de x.
2. Justifier que l'expression de \mathrm{B}(x) en fonction de x est \text{B}(x)=-15 x^{3}+120 x^{2}+180 x
3. Pour tout nombre réel x appartenant à l'intervalle [1 \: ; 10], déterminer \mathrm{B}^{\prime}(x).
4. a. Montrer que, pour tout x \in[1 \: ; 10] \: :
\mathrm{B}^{\prime}(x)=-15(x-6)(3 x+2)
b. En déduire le signe de la fonction \text{B}^{\prime} sur l'intervalle [1 \: ; 10] en s'aidant du tableau de signe suivant.
5. En utilisant la question précédente, construire le tableau de variations de la fonction \text{B} sur l'intervalle [1 \: ; 10].
6. Déterminer la longueur de tissu que l'entreprise doit produire et vendre chaque jour pour que le bénéfice réalisé soit maximal. Que vaut ce bénéfice maximal ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 95
Défi
Démontrer, dans le cas général, que si une fonction f est croissante sur un intervalle \text{I}, alors sa dérivée est positive pour tout x \in \text{I}. On pourra utiliser des arguments graphiques ou le calcul de taux de variation.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 96
Défi
Comparaison coût moyen et coût marginal.
Expliquer pourquoi on dit que « lorsque le coût marginal est supérieur au coût moyen, alors le coût moyen est croissant ».
Expliquer pourquoi on dit que « lorsque le coût marginal est supérieur au coût moyen, alors le coût moyen est croissant ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 97
Défi
Commenter cette phrase :
« On admet que le coût moyen est minimal lorsqu'il est égal au coût marginal. »
« On admet que le coût moyen est minimal lorsqu'il est égal au coût marginal. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 98
Casse-tête
Tracer la courbe représentative :
1. d'une fonction négative dont la dérivée est négative ;
2. d'une fonction positive dont la dérivée est négative et décroissante ;
3. d'une fonction négative dont la dérivée est positive et décroissante.
1. d'une fonction négative dont la dérivée est négative ;
GeoGebra
2. d'une fonction positive dont la dérivée est négative et décroissante ;
GeoGebra
3. d'une fonction négative dont la dérivée est positive et décroissante.
GeoGebra
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
