Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 6
L'essentiel
Trigonométrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiche méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Convertir des degrés en radian et réciproquement
- On construit un tableau de proportionnalité dans lequel on place la valeur connue et les valeurs \pi et 180°, étant donné que \pi rad correspond à 180°.
- On utilise ensuite la règle de proportionnalité (produit en croix).
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Déterminer la mesure principale d'un angle orienté
- Si la mesure de l'angle orienté appartient à ]-\pi \: ; \pi], alors c'est la mesure principale.
- Si la mesure est inférieure ou égale à -\pi, alors on ajoute 2\pi autant de fois que nécessaire pour obtenir une mesure appartenant à ]-\pi \: ; \pi].
- Si la mesure est strictement supérieure à \pi, alors on soustrait 2\pi autant de fois que nécessaire pour obtenir une mesure appartenant à ]-\pi \: ; \pi].
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Calculer le cosinus ou le sinus d'un nombre réel
- On commence par repérer les valeurs remarquables qui seront utiles.
- En s'aidant du cercle trigonométrique et des symétries, on détermine la valeur recherchée.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Résoudre une équation de la forme \bm{\cos (x)=a} ou \bm{\sin (x)=a (a\in [-1\: ;1])}
- On cherche les valeurs de x de l'intervalle ]-\pi \: ; \pi] qui vérifient l'équation.
- Pour cela, on trace le cercle trigonométrique et on place la valeur a apparaissant dans l'équation sur l'axe des abscisses ou des ordonnées selon que l'équation fait apparaître du cosinus ou du sinus.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Étudier une fonction de la forme \bm{t \mapsto \mathbf{A} \cos (\omega t+\varphi)}
- |\mathrm{A}| correspond à l'écart entre le maximum de la fonction et l'axe des abscisses.
- La période \text{T} s'obtient soit graphiquement, soit par la relation \mathrm{T}=\frac{2 \pi}{\omega}.
- La pulsation \omega s'obtient par la relation \omega=\frac{2 \pi}{\mathrm{T}}.
Auto‑évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
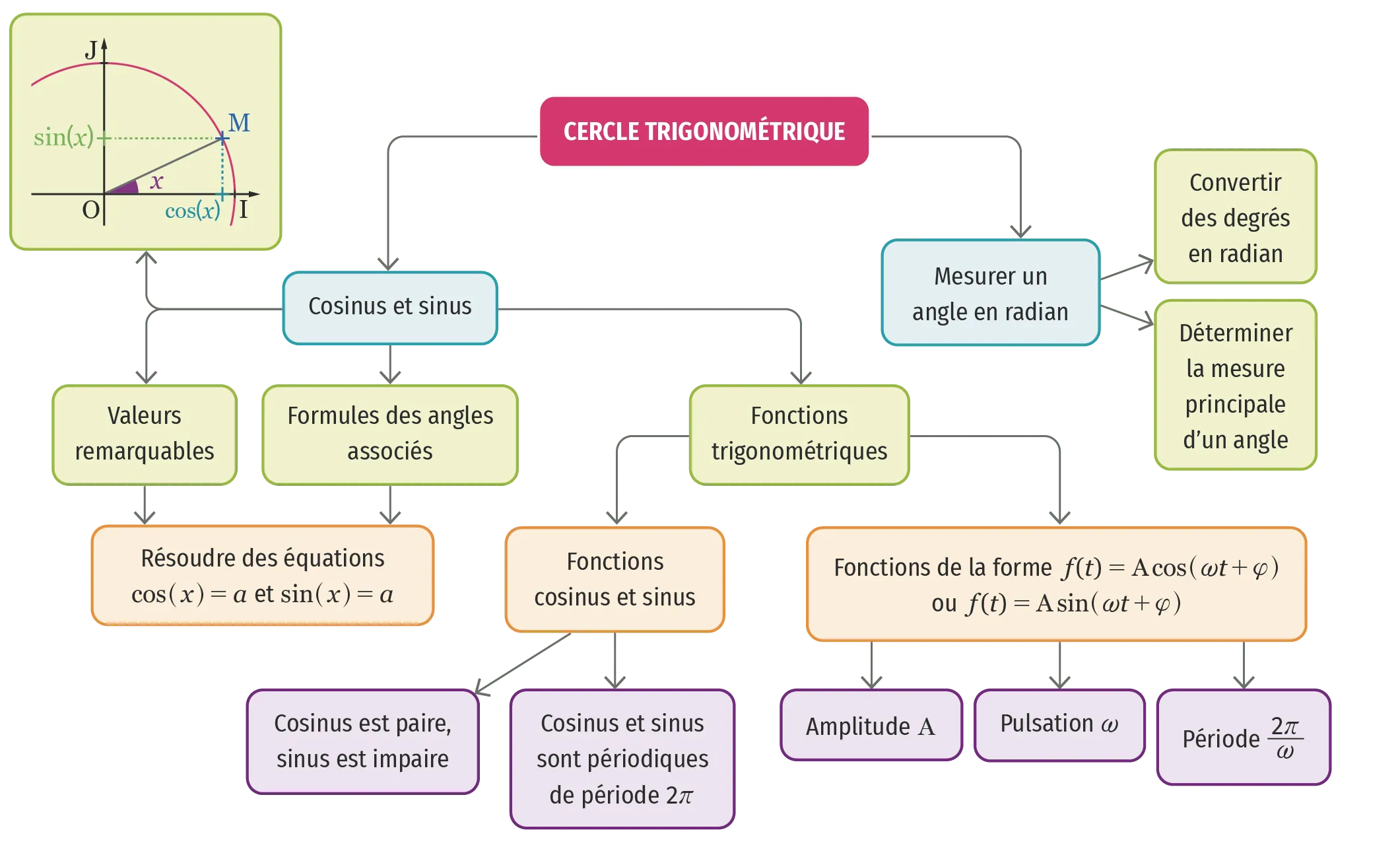
Carte mentale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah