Synthèse

On représente la Terre par un point \text{T}, la Lune par un point \text{L} et le Soleil par un point \text{S}. On dit que la Lune est visible en quadrature lorsque exactement la moitié du disque lunaire est visible depuis la Terre. On parle de premier quartier de lune et de dernier quartier de lune.

Autrement dit, cela se produit lorsque \widehat{\text{SLT}} = 90\degree. On observe par ailleurs depuis la Terre que, dans cette position, \widehat{\text{LTS}} = 89{,}853\degree.

Calculer le rapport de longueur \frac{\text { TS }}{\text { TL }} puis interpréter le résultat par une phrase.

On suspend une masse m à un ressort. On note y la hauteur relative de la masse. La valeur y = 0 correspond à l'équilibre lorsque la masse est immobile.

On amène la masse à 10 cm de hauteur, puis on la lâche. On suppose ici que le modèle est parfait et qu'il n'y a pas d'amortissement des oscillations, autrement dit que les oscillations restent les mêmes au cours du temps, sans être atténuées.

Les oscillations pour t \geqslant 0 (t en seconde) sont données par y(t)=10 \cos (3 t).


1. Pour quel temps t_1 la masse va-t-elle passer pour la première fois par sa position d'équilibre y = 0 ?

2. Pour quel temps t_2 la masse va-t-elle repasser pour la deuxième fois par sa position d'équilibre ?

3. Quelle est la période des oscillations de la masse ?

4. Quelle sera la hauteur maximale de la masse ? Et la hauteur minimale ?

Un héron repère un poisson dans l'eau (voir ci-dessous). Il souhaite plonger pour l'attraper, mais il sait que lorsque la lumière passe d'un milieu à un autre, elle subit une déviation. Il ne doit donc pas aller « tout droit vers le poisson ».




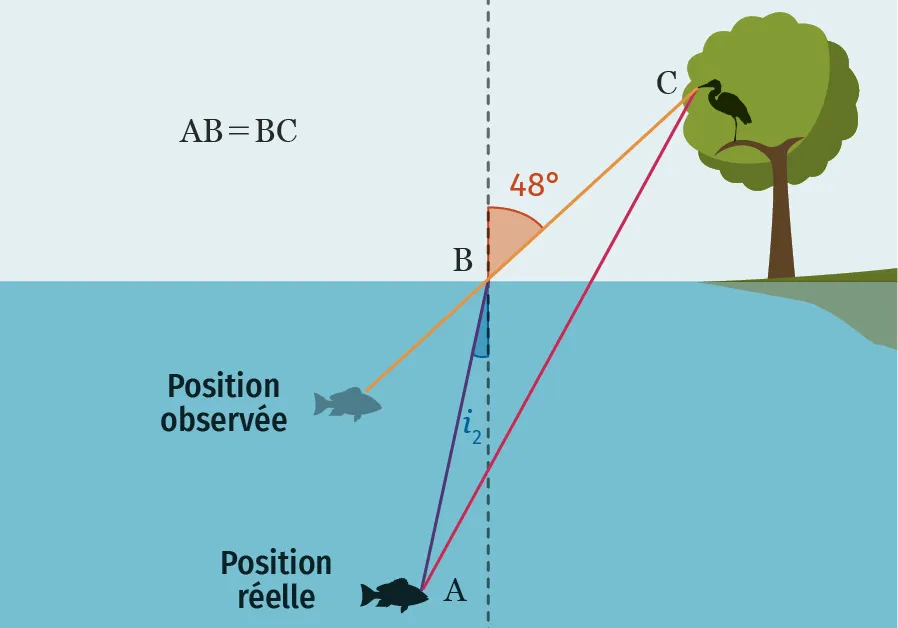
Le héron souhaite attraper sa proie en se dirigeant en ligne droite en suivant le segment [\mathrm{CA}]. On suppose le triangle \text{ABC} isocèle en \text{B}.

1. Que peut-on dire des angles \widehat{\mathrm{BCA}} et \widehat{\mathrm{BAC}} ?

2. Déterminer l'angle i_2 approché au degré près.

3. En déduire la valeur, arrondie au degré près, de l'angle \widehat{\mathrm{BCA}}.

Dans un repère orthonormé de centre \text{O}, on représente les extrémités des pales d'une éolienne par les points \text{A}, \text{B} et \text{C}. Les trois pales sont de même longueur, à savoir \mathrm{OA}=\mathrm{OB}=\mathrm{OC}=50 m, et l'éolienne est symétrique, c'est-à-dire que les angles \widehat{\mathrm{BOA}}, \widehat{\mathrm{AOC}} et \widehat{\mathrm{COB}} sont égaux. Sur le dessin, \text{A} a pour coordonnées \mathrm{A}(0 \: ; 50).


1. a. Justifier que \widehat{\mathrm{BOA}}=\frac{2 \pi}{3}.

b. Déterminer la mesure de l'angle \widehat{\mathrm{BOI}} en radian, puis une mesure de l'angle (\overrightarrow{\mathrm{OI}}, \overrightarrow{\mathrm{OB}}).

c. En déduire les coordonnées du point \text{B}.

2. En utilisant la même méthode, calculer les coordonnées du point \text{C}.

3. L'hélice tourne à une vitesse de 15 tours par minute.
Déterminer la vitesse de déplacement du point \text{A} de l'hélice en km/h. On arrondira à l'unité.

On a représenté dans un repère (\mathrm{O}\: ; \mathrm{I}, \mathrm{J}) le cercle trigonométrique.
On rappelle les formules de trigonométrie dans le triangle rectangle étudiées au collège : \cos (\theta)=\frac{\text { côté adjacent }}{\text { hypoténuse }} et \sin (\theta)=\frac{\text { côté opposé }}{\text { hypoténuse }}.


1. a. Quelle est la longueur de la diagonale d'un carré de côté 1 ?

b. Ici, on utilise le carré \text{OABC}. Que vaut cette diagonale ?

c. Par proportionnalité, en déduire la longueur des côtés du carré \text{OABC}.

2. On travaille maintenant dans le triangle \text{OID}.
a. Justifier que \text{OID} est équilatéral

b. On note \text{E} le pied de la hauteur issue de \text{D}. Quelle est la longueur \text{OE} ?

c. En déduire \cos \left(\frac{\pi}{3}\right).

d. En utilisant la relation \cos ^{2}(\theta)+\sin ^{2}(\theta)=1, déterminer \sin \left(\frac{\pi}{3}\right).

3. En utilisant un raisonnement similaire à la question 2., déterminer \cos \left(\frac{\pi}{6}\right) et \sin \left(\frac{\pi}{6}\right).

On considère un triangle \text{ABC} non aplati dont les longueurs et les angles sont définis comme sur la figure ci-dessous.

1. Montrer que l'aire \mathcal{A} de \text{ABC} est donnée par la formule suivante : \mathcal{A}=\frac{b c \sin (\alpha)}{2}.

2. En écrivant deux formules similaires pour calculer \mathcal{A}, en déduire que \frac{a}{\sin (\alpha)}=\frac{b}{\sin (\beta)}=\frac{c}{\sin (\gamma)}.

Cette formule est appelée loi des sinus. Elle a été énoncée et démontrée par des mathématiciens arabes (XI^e-XIII^e siècles) et en particulier par Abu Nasr Mansur et Nasir al-Din-al-Tusi.

On considère un triangle \text{ABC} tel que \text{AB} = 5, \text{AC} = 6 et \widehat{\mathrm{BAC}}=60\degree. Déterminer la longueur \text{BC} (on cherche une valeur exacte).

Indication

On pourra utiliser la hauteur \text{(BH)} issue de \text{B}.