Chapitre 3
Entraînement
Calcul littéral
Factoriser une expression littérale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Factoriser une expression littérale
Propriétés :
1. Simple distributivité : Soient k, a et b des nombres quelconques.
{\color{green}k} \times {\color{red}a}+{\color{green}k} \times {\color{blue}b}={\color{green}k} \times({\color{red}a}+{\color{blue}b})
2. Identité remarquable : Soient a et b des nombres quelconques.
{\color{red}a^{2}}-{\color{blue}b^{2}}=({\color{red}a}+{\color{blue}b})({\color{red}a}-{\color{blue}b})
❯ Retrouvez un
1. Simple distributivité : Soient k, a et b des nombres quelconques.
{\color{green}k} \times {\color{red}a}+{\color{green}k} \times {\color{blue}b}={\color{green}k} \times({\color{red}a}+{\color{blue}b})
2. Identité remarquable : Soient a et b des nombres quelconques.
{\color{red}a^{2}}-{\color{blue}b^{2}}=({\color{red}a}+{\color{blue}b})({\color{red}a}-{\color{blue}b})
❯ Retrouvez un
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 12 [Mod.8 - Cal.4]
Factoriser les expressions suivantes.
1. \mathrm{A}=2 x-16
2. \mathrm{B}=5 x^{2}+9 x
3. \mathrm C=-3 x^{2}+8 x
4. \mathrm{D}=-8 x-64
1. \mathrm{A}=2 x-16
2. \mathrm{B}=5 x^{2}+9 x
3. \mathrm C=-3 x^{2}+8 x
4. \mathrm{D}=-8 x-64
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13 [Mod.8 - Cal.4]
Factoriser les expressions suivantes.
1. \mathrm A=4 x^{2}-36 x
2. \mathrm{B}=7 x-7
3. \mathrm{C}=72 x^{2}+45 x
4. \mathrm{D}=-3 x^{2}+x
1. \mathrm A=4 x^{2}-36 x
2. \mathrm{B}=7 x-7
3. \mathrm{C}=72 x^{2}+45 x
4. \mathrm{D}=-3 x^{2}+x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14 [Mod.8 - Cal.4]
Associer à chaque expression toutes les expressions qui lui sont égales.
4 a^{2}+16 a
2 a^{3}+8 a^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 15
[Mod.8 - Cal.4]
Compléter les expressions suivantes.
1. (x+8)(x-8)=x^{2}-
2. (3 x-4)(3 x+4)=-16
3. (7 x+9)(7 x-9)=-
4. (-1)(+1)=25 x^{2}-1
5. (+)(-)=49 x^{2}-9
6. (-10)(+10)=16 x^{2}-
1. (x+8)(x-8)=x^{2}-
2. (3 x-4)(3 x+4)=
3. (7 x+9)(7 x-9)=
4. (
5. (
6. (
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 16
[Mod.8 - Cal.4]
Factoriser les expressions suivantes.
1. \mathrm A=x^{2}-36
2. \mathrm{B}=x^{2}-121
3. \mathrm C=36 x^{2}-4
4. \mathrm{D}=9 x^{2}-1
1. \mathrm A=x^{2}-36
2. \mathrm{B}=x^{2}-121
3. \mathrm C=36 x^{2}-4
4. \mathrm{D}=9 x^{2}-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 17
[Mod.8 - Cal.4]
Factoriser les expressions suivantes.
1. \mathrm{A}=2 x^{2}-3 x
2. \mathrm{B}=14 x^{2}-28 x
3. \mathrm C=25 x^{2}-64
4. \mathrm{D}=100 x^{2}-9
5. \mathrm{E}=16 x^{2}-4 x
6. \mathrm F=x^{2}-7
1. \mathrm{A}=2 x^{2}-3 x
2. \mathrm{B}=14 x^{2}-28 x
3. \mathrm C=25 x^{2}-64
4. \mathrm{D}=100 x^{2}-9
5. \mathrm{E}=16 x^{2}-4 x
6. \mathrm F=x^{2}-7
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 18 [Mod.8 - Rais.4 - Cal.4]
Voici un programme de calcul écrit en Scratch.

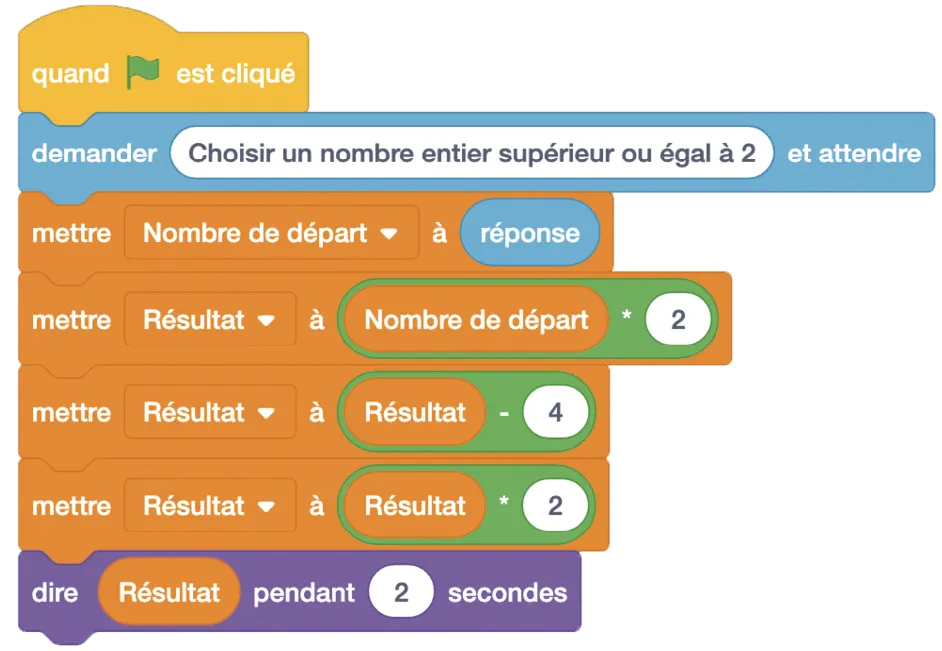
1. Vérifier que, si l'on choisit 5 comme nombre de départ, on obtient 12 .
2. Calculer le nombre obtenu si on choisit 8 comme nombre de départ.
3. Soit n un entier supérieur ou égal à 2. Exprimer, en fonction de n, le résultat du programme de calcul
4. Quel nombre doit-on choisir au départ pour obtenir 28 ? Justifier.
5. Développer et réduire l'expression obtenue dans la question 3. En déduire que, quelque soit le nombre entier supérieur ou égal à 2 choisi, on obtient toujours un multiple de 4.


1. Vérifier que, si l'on choisit 5 comme nombre de départ, on obtient 12 .
2. Calculer le nombre obtenu si on choisit 8 comme nombre de départ.
3. Soit n un entier supérieur ou égal à 2. Exprimer, en fonction de n, le résultat du programme de calcul
4. Quel nombre doit-on choisir au départ pour obtenir 28 ? Justifier.
5. Développer et réduire l'expression obtenue dans la question 3. En déduire que, quelque soit le nombre entier supérieur ou égal à 2 choisi, on obtient toujours un multiple de 4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 19 [Mod.8 - Cal.4]
Factoriser les expressions suivantes.
1. \mathrm{A}=(x+2)^{2}-9
2. \mathrm{B}=4 x^{2}-(x-1)^{2}
3. \mathrm C=(3 x+4)^{2}-(x-3)^{2}
1. \mathrm{A}=(x+2)^{2}-9
2. \mathrm{B}=4 x^{2}-(x-1)^{2}
3. \mathrm C=(3 x+4)^{2}-(x-3)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 20 [Mod.8 - Cal.4]
Factoriser les expressions suivantes.
1. \mathrm A=(x+2)(x-1)+(2 x+3)(x-1)
2. \mathrm{B}=(3 x+5)(x-2)-(3 x+5)(4 x-6)
3. \mathrm C=(7 x-5)(2 x-1)+(2 x-1)^{2}
1. \mathrm A=(x+2)(x-1)+(2 x+3)(x-1)
2. \mathrm{B}=(3 x+5)(x-2)-(3 x+5)(4 x-6)
3. \mathrm C=(7 x-5)(2 x-1)+(2 x-1)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 21Le coin des experts
Factoriser l'expression suivante.
\text{A}=(3 x+1)(2 x+4)-4 x^{2}+16
\text{A}=(3 x+1)(2 x+4)-4 x^{2}+16
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

