Voici un questionnaire à choix multiples. Pour chaque question, cocher la (ou les) bonne(s) réponse(s).

1. L'expression 4 x-8 est égale à :

a. 4(x-2)

b. (6 x-1)(2 x+7)

c. (6 x-1)-(2 x+7)

2. La forme développée et réduite de (5 x-9)(-x+4) est :

a. 5 x^{2}+29 x+36

b. -5 x^{2}+29 x-36

c. -5 x^{2}+11 x-36

3. Une forme factorisée de 4 x^{2}-25 est :

a. x(4 x-25)

b. (4 x+5)(4 x-5)

c. (2 x-5)(2 x+5)

4. On considère le programme de calcul ci-dessous.

\boxed{ \begin{array} { r|l } 1 & \text{Choisir un nombre} \\ 2 & \text{Multiplier par 8} \\ 3 & \text{Retrancher 6} \\ 4 & \text{Multiplier le résultat par 2} \\ \end{array} }

On peut alors dire que :

a. si on choisit -5 au départ, on obtient -92 ;

b. si on choisit x au départ, l'expression du résultat final est 8 x-12 ;

c. si on choisit un entier supérieur ou égal à 1 au départ, on obtient toujours un multiple de 4 .

5. Soit x, un nombre positif. On considère les deux figures ci-dessous.
On peut alors dire que :

a. l'aire du carré est toujours égale à x^{2}+9 quelle que soit la valeur de x;

b. le périmètre du carré est toujours égal à celui du rectangle quelle que soit la valeur de x;

c. l'aire du carré est toujours égale à celle du rectangle quelle que soit la valeur de x.

Donner les dimensions d'une figure usuelle dont l'aire est égale à x^{2}-1, où x est un nombre supérieur ou égal à 2 .

D'après brevet, Métropole, septembre 2020
On considère le programme de calcul suivant.

\boxed{ \begin{array} { r|l } 1 & \text{Choisir un nombre} \\ 2 & \text{Ajouter 7 à ce nombre} \\ 3 & \text{Soustraire 7 au nombre choisi au départ} \\ 4 & \text{Multiplier les deux résultats précédents} \\ 5 & \text{Ajouter 50} \\ \end{array} }

1. Montrer que si le nombre choisi au départ est 2, alors le résultat obtenu est 5.

2. Un élève s'aperçoit qu'en calculant le double de 2 et en ajoutant 1 , il obtient 5, le même résultat que celui qu'il a obtenu à la question 1 . Il pense alors que le programme de calcul revient à calculer le double du nombre de départ et à ajouter 1. A-t-il raison ?

Voici un programme de calcul écrit en Scratch.

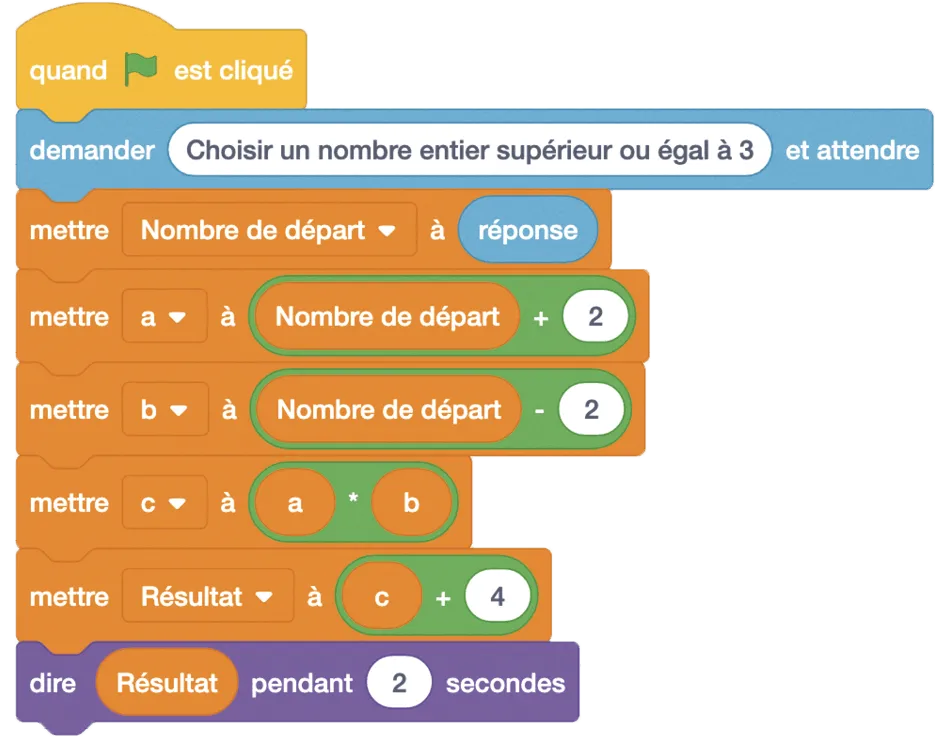
1. Vérifier que si l'on choisit 3 comme nombre au départ, le programme donne 9 comme résultat.

2. Calculer le nombre obtenu si on choisit 7 comme nombre de départ.

3. Soit n un entier supérieur ou êgal à 2 . Exprimer, en fonction de n, le résultat du calcul.

4. Séréza pense que l'on peut trouver le résultat final en une seule opération. A-t-elle raison ? Justifier.

5. Quel nombre doit-on choisir au dêpart pour obtenir 196 ? Justifier.

1. Donner les résultats des calculs suivants.
a. \mathrm A=1 \times 3-2^{2}

b. \mathrm{B}=2 \times 4-3^{2}

c. \mathrm C=6 \times 8-7^{2}

2. a. Proposer deux autres expressions du même type et les calculer.

b. Quelle conjecture peut-on faire ?

3. Soit n un nombre entier. Dêmontrer la conjecture de la question 2. b. .

1. Soient a et b deux nombres quelconques. Dêmontrer que (a+b)^{2}=a^{2}+2 a b+b^{2}.

2. Cette égalitê est également une identité remarquable. Développer et réduire, en utilisant cette identité, les expressions suivantes.
a. \mathrm{A}=(x+4)^{2}

b. \mathrm{B}=(3 x+7)^{2}

Réviser les notions de ce chapitre grâce à cette activité interactive.
Pour une utilisation optimale, réaliser l'activité en plein écran.