Nombres et calculs

On considère les schémas ci-dessous. Le rectangle violet représente 1 unité.


1. Compléter la phrase suivante.

Pour représenter la fraction \frac{12}{3}, on coupe l'unité en

parts égales et on en prend

parts.

2. Sur le premier schéma, représenter la fraction \frac{12}{3}.

3. Partager les douze unités du second schéma en trois parts égales. Combien d'unités y a-t-il par part ?

4. Comparer les deux schémas. Que constate-t-on ?

5. En déduire une égalité entre une fraction \frac{12}{3} et une opération connue.

6. Si a et b sont deux entiers avec b non nul, expliquer à quelle opération est égale la fraction \frac{a}{b}.

On souhaite déterminer 4 \times \frac{5}{4}. On dispose pour cela de la demi-droite graduée ci-dessous.


1. Repérer la fraction \frac{5}{4} sur cette demi-droite.

2. À l'aide des outils, tracer un segment partant de l'origine qui repère la longueur correspondant à \frac{5}{4}.

3. À partir de l'origine, reporter quatre fois la longueur correspondant à \frac{5}{4} en copiant et collant le segment tracé.
4. Que vaut 4 \times \frac{5}{4} ?

1. Observer l'exemple.
Le produit 147,32 \times 10 correspond à 147,32 dizaines. On utilise ensuite le tableau de numération.


Ainsi, 147,32 \times 10 = 1~473,2. En multipliant par 10, on obtient donc un nombre 10 fois plus grand.

2. Calculer de la même manière 147,32 \times 0,1. Qu'observe-t-on ?

3. Quel est le résultat de la multiplication 36,4 \times 0,01 ?

1. a. Quel calcul devrait-on poser pour calculer l'aire du rectangle \mathrm{ABCD} ? Quelle serait l'unité ?

b. Convertir les longueurs en cm, puis calculer l'aire du rectangle.

2. On souhaite maintenant calculer l'aire du rectangle en dm².
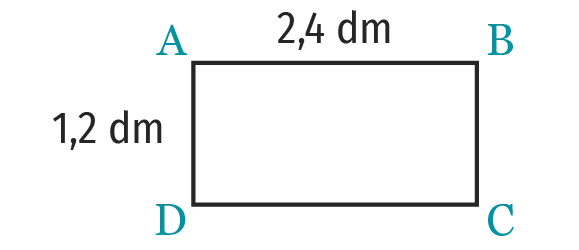
a. Par combien doit-on multiplier les cm pour obtenir des dm ?

b. Expliquer pourquoi on peut écrire :
\text{Aire} (\mathrm{ABCD})=24~\times~0,1~\times 12~\times 0,1~\mathrm{dm}^2.

c. À l'aide de ce calcul, justifier l'égalité : 2,4 \times 1,2 = 2,88.

Coup de pouce

On peut changer l'ordre des facteurs dans une multiplication.