Thème 1 : Nombres et calculs
Fiche 24
Modéliser des phénomènes aléatoires et calculer des probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définitions
- Une expérience est aléatoire lorsque les résultats possibles, appelés issues, sont connus sans que l'on puisse déterminer lequel sera effectivement réalisé.
- Un événement est un ensemble d'issues.
Exemple : Le lancer d'une pièce de monnaie ou d'un dé à 6 faces sont des expériences aléatoires. Les issues peuvent être « Pile » ou « Face » pour la première et « Obtenir 1 », « Obtenir 2 », ... , « Obtenir 6 » pour la seconde.
Définition
La probabilité d'un événement mesure la chance qu'un événement se produise. C'est un nombre compris entre 0 et 1.
Propriété
Plus la probabilité d'un événement est proche de 0, moins il a de chances de se produire. Inversement, plus la probabilité d'un événement est proche de 1, plus il a de chances de se produire.

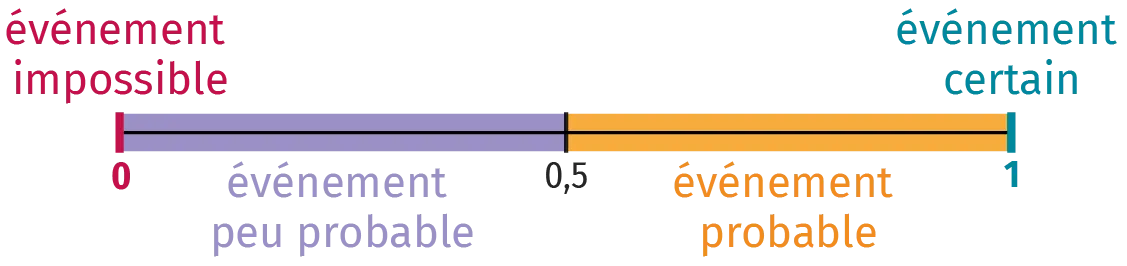
Propriété
Lorsque chaque issue a la même chance de se produire, on peut calculer la probabilité d'un événement par la formule :
\frac{\text{nombre de cas favorables}}{\text{nombre de cas possibles}}.
Exemples :
1. En jouant à pile ou face, la probabilité d'obtenir pile est une chance sur deux, soit \frac{1}{2} c'est-à-dire 50~\%.
2. En lançant un dé à 6 faces équilibré, la probabilité d'obtenir 3 est une chance sur 6, soit \frac{1}{6}.
1. En jouant à pile ou face, la probabilité d'obtenir pile est une chance sur deux, soit \frac{1}{2} c'est-à-dire 50~\%.
2. En lançant un dé à 6 faces équilibré, la probabilité d'obtenir 3 est une chance sur 6, soit \frac{1}{6}.
- Remarque : Lorsque l'on répète deux fois une même expérience aléatoire, il est parfois pratique de représenter les issues à l'aide d'un arbre de probabilités ou d'un tableau à double entrée.
Exemples :
1. On joue à pile ou face deux fois de suite. On obtient alors quatre issues possibles qui ont toutes la même probabilité de se produire : \left(\mathrm{P}~\text{;}~\mathrm{F}\right) ou \left( \mathrm{P}~\text{;}~\mathrm{P}\right) ou \left( \mathrm{P}~\text{;}~\mathrm{F}\right) ou \left(\mathrm{P}~;~ \mathrm{P}\right). On peut représenter la situation à l'aide d'un arbre.

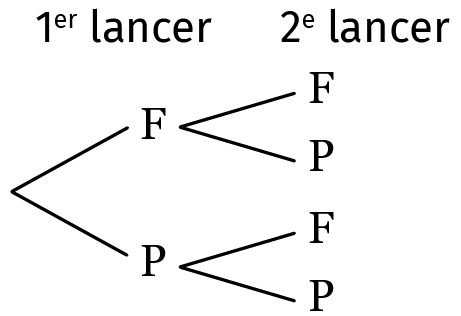
1. On joue à pile ou face deux fois de suite. On obtient alors quatre issues possibles qui ont toutes la même probabilité de se produire : \left(\mathrm{P}~\text{;}~\mathrm{F}\right) ou \left( \mathrm{P}~\text{;}~\mathrm{P}\right) ou \left( \mathrm{P}~\text{;}~\mathrm{F}\right) ou \left(\mathrm{P}~;~ \mathrm{P}\right). On peut représenter la situation à l'aide d'un arbre.


2. On lance deux fois de suite un dé à quatre faces comme ci-contre. On obtient 16 issues possibles qui ont toutes la même probabilité.




| 2e tour | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1er tour | 1 | (1 ; 1) | (1 ; 2) | (1 ; 3) | (1 ; 4) |
| 2 | (2 ; 1) | (2 ; 2) | (2 ; 3) | (2 ; 4) | |
| 3 | (3 ; 1) | (3 ; 2) | (3 ; 3) | (3 ; 4) | |
| 4 | (4 ; 1) | (4 ; 2) | (4 ; 3) | (4 ; 4) | |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Lorsque 23 personnes sont rassemblées, il
existe un peu plus d'une chance sur deux qu'au
moins deux personnes, parmi les 23, fêtent leur
anniversaire le même jour.
▸ Plus d'.
▸ Plus d'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. \frac{1}{4}=
2. 3,2 \div 100 =
3. 1~\text{s}= \mathrm{h}
2. 3,2 \div 100 =
3. 1~\text{s}=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
On donne ci-dessous différents événements associés à une expérience aléatoire.
Indiquer si ces événements sont impossibles, peu probables, probables ou certains.
Indiquer si ces événements sont impossibles, peu probables, probables ou certains.
| Événement | Impossible ? Peu probable ? Probable ? Certain ? |
|---|---|
| Obtenir le bon tirage au loto. | |
| Obtenir 6 en lançant un dé à six faces. | |
| Obtenir une boule verte dans un sac contenant sept boules vertes et une seule boule jaune. | |
| Obtenir au moins 2 lorsqu'on fait la somme des résultats obtenus à deux lancers de dés. | |
| Obtenir quinze fois de suite « Pile » en lançant quinze fois une pièce de monnaie. | |
| Obtenir une consonne en choisissant au hasard une lettre de l'alphabet. | |
| Obtenir un ours orange en choisissant un bonbon au hasard de ce sac de bonbons.   |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
On s'intéresse à un jeu de 32 cartes dont on voit les cartes ci-dessous.
On mélange le paquet et on tire une carte au hasard.


1. Combien a-t-on d'issues possibles ?
2. Donner les probabilités des événements suivants.
3. Positionner les probabilités sur l'axe ci-dessous.
4. Préciser alors les événements impossibles, peu
probables, probables et certains.
On mélange le paquet et on tire une carte au hasard.


1. Combien a-t-on d'issues possibles ?
| \mathrm{A} : « On tire un cœur. » | \mathrm{B} : « On tire un neuf. » | ||
| \mathrm{C} : « On tire une tête (valet, dame ou roi) noire. » | \mathrm{D} : « On tire un cinq. » | ||
| \mathrm{E} : « On tire l'as de pique. » | \mathrm{F} : « On ne tire pas un as. » |
3. Positionner les probabilités sur l'axe ci-dessous.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Pour chaque affirmation, indiquer si elle est vraie ou fausse.
| La probabilité d'obtenir « Pile » lors du lancer d'une pièce de monnaie est de 50 %. | |
|---|---|
| Si on lance une pièce 10 fois, on obtient toujours 5 fois « Pile » et 5 fois « Face ». | |
| La probabilité d'obtenir un 6 avec un dé à six faces est de \frac{1}{6}. | |
| La probabilité d'obtenir un nombre pair avec un dé à six faces est de \frac{1}{3}. | |
| Si on lance un dé 6 fois, on obtient forcément un 6 au moins une fois. | |
| Si on pioche une boule dans un sac contenant 2 boules blanches et 3 noires, la probabilité de tirer une boule blanche sera de \frac{2}{3}. | |
| On lance un dé à 6 faces. La probabilité d'obtenir au moins 3 est égale à \frac{1}{2}. |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Dans chaque cas, vaut-il mieux choisir un dé à 4 faces, un dé à 6 faces ou un dé à 8 faces ? Justifier.
1. On veut obtenir la face numérotée 1.
2. On veut obtenir un nombre impair.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Copie d'élève
Copie d'élève
Un élève a résolu l'exercice suivant.
On joue à pile ou face en lançant deux pièces de monnaie. Déterminer la probabilité d'obtenir une fois « Pile » et une fois « Face ».
On joue à pile ou face en lançant deux pièces de monnaie. Déterminer la probabilité d'obtenir une fois « Pile » et une fois « Face ».
Si on lance deux pièces de monnaie et que l'on regarde les résultats, on peut obtenir :
- deux fois pile
- deux fois face
- une fois pile et une fois face
Ainsi, sur les trois issues possibles, une seule permet d'avoir un pile et un face.
La probabilité d'obtenir un pile et un face est \frac{1}{3}.
- deux fois pile
- deux fois face
- une fois pile et une fois face
Ainsi, sur les trois issues possibles, une seule permet d'avoir un pile et un face.
La probabilité d'obtenir un pile et un face est \frac{1}{3}.
1. Compléter l'arbre représentant la situation.
2. Déterminer la probabilité d'obtenir deux fois face, puis celle d'obtenir deux fois pile.
3. Répondre au problème posé à l'élève, puis expliquer son erreur.
3. Répondre au problème posé à l'élève, puis expliquer son erreur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
On lance deux dés à 4 faces et on s'intéresse à la somme des numéros des faces obtenues.
1. Compléter le tableau à double entrée en indiquant la somme obtenue.
2. Est-il plus probable d'obtenir 4 ou d'obtenir 7 ?
1. Compléter le tableau à double entrée en indiquant la somme obtenue.
| 2e dé | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1er dé | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
2. Est-il plus probable d'obtenir 4 ou d'obtenir 7 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
On a effectué le lancer d'un dé à 6 faces 100 fois de suite. Voici les résultats obtenus.

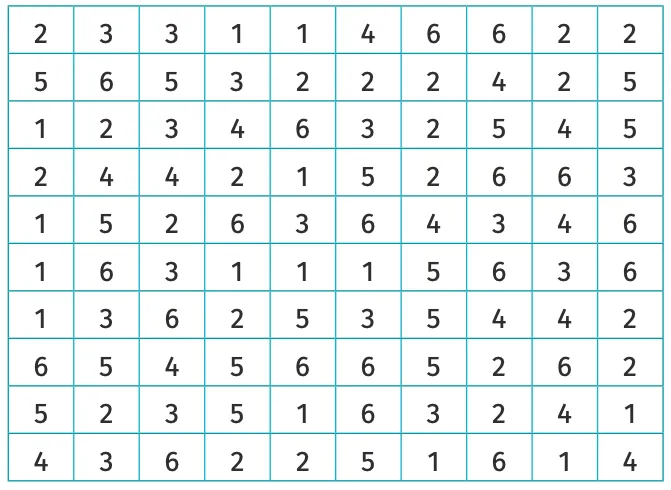
1. Compléter le tableau suivant.
2. Les résultats sont-ils cohérents avec les
probabilités d'obtenir chacune des faces ?


1. Compléter le tableau suivant.
Face obtenue
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
Nombre
d'apparitions
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Dans un sac contenant des boules vertes et des boules bleues, on tire au hasard une boule et on regarde sa couleur. On replace ensuite la boule dans le sac et on mélange.
1. Sachant que la probabilité d'obtenir une boule verte est \frac{2}{5}, colorier les boules du sac.


2. Compléter la phrase suivante.
La probabilité de tirer une boule bleue est.
3. Ana a tiré trois fois de suite une boule verte. Aura-t-elle plus de chances de tirer une boule verte au prochain tirage ?
1. Sachant que la probabilité d'obtenir une boule verte est \frac{2}{5}, colorier les boules du sac.


2. Compléter la phrase suivante.
La probabilité de tirer une boule bleue est
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Énigme
Nolan participe à un jeu et il doit obtenir du jaune pour gagner. Il doit soit piocher au hasard une bille dans un sac, soit lancer un dé. Que doit-il choisir ?
Informations sur le dé :
• Il possède 6 faces.
• Il contient des faces jaunes et vertes.
• Il a deux faces vertes de plus que de faces jaunes.
Doit-il plutôt choisir de tirer une bille du sac ou de lancer le dé coloré ?
Informations sur le sac :
• Il contient des billes rouges, vertes et jaunes.
• Il contient 10 billes rouges.
• La probabilité de tirer une bille rouge est de \frac{1}{3}.
• Il contient 8 billes vertes.
• Il contient des billes rouges, vertes et jaunes.
• Il contient 10 billes rouges.
• La probabilité de tirer une bille rouge est de \frac{1}{3}.
• Il contient 8 billes vertes.
Informations sur le dé :
• Il possède 6 faces.
• Il contient des faces jaunes et vertes.
• Il a deux faces vertes de plus que de faces jaunes.
Doit-il plutôt choisir de tirer une bille du sac ou de lancer le dé coloré ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


