Construire des collections jusqu'à 599

Partir d'une écriture chiffrée pour produire une collection va engager un travail sur la prise d'informations directe à partir de l'écriture du nombre. Par exemple, en tenant compte des relations entre unités de numération, l'écriture 165 nous dit que le nombre est composé de 1 C, 6 D et 5 U, ou 16 D et 5 U ou 1 C et 65 U. Il est important de jongler entre les différentes écritures d'un même nombre afin que les élèves s'habituent à passer de l'une à l'autre. Cet apprentissage est essentiel pour une compréhension fine de notre système de numération et pour développer des stratégies de calcul.

Comparer deux nombres inférieurs à 100
Faire rappeler la signification des symboles < et >.
Projeter et distribuer la carte rituel P1-4.
Demander aux élèves d'écrire les signes < ou > entre les nombres comparés.
Corriger devant les élèves et faire expliciter les réponses.

Variable didactique
Énoncer oralement les nombres ou les proposer décomposés en dizaines et unités.

Multiplicatif : recherche du produit
Le boulanger prépare 4 paquets de 10 croissants. Trouve le nombre de croissants préparés.

Quelle situation correspond à l'énoncé ?
Projeter le problème intercalaire et les situations proposées. Échanger sur celle qui correspond à l'énoncé et en expliciter les raisons.

Afin de rappeler la séquence précédente, faire réfléchir l'ensemble de la classe durant une minute, puis solliciter au moins deux élèves pour l'expliciter. Réviser notamment la lecture et l'écriture des nombres supérieurs à 100.

« Vous avez appris à organiser des collections en centaines, dizaines et unités pour les dénombrer. Aujourd'hui, c'est vous qui allez représenter des collections. »

« Vous allez représenter 453 dans votre cahier de recherche. Vous pouvez vous aider du matériel multibase. »

Circuler pour valider les procédures des élèves en réussite et aider ceux qui en ont besoin. Proposer aux élèves ayant terminé de comparer leur résultat par deux puis de chercher d'autres façons de représenter le nombre.

Procédures possibles :

• dessiner individuellement les 453 unités ;
• compter de 10 en 10 puis de 1 en 1 jusqu'à 453 pour dessiner 45 dizaines et 3 unités ;
• compter de 100 en 100, puis de 10 en 10, puis de 1 en 1 jusqu'à 453 pour dessiner 4 centaines, 5 dizaines et 3 unités ;
• lire directement le nombre de centaines, dizaines et unités isolées dans l'écriture chiffrée et les représenter.

Expliciter que les procédures 1 et 2 sont à la fois lentes et peu sûres : il est compliqué de vérifier son résultat.

D'autres procédures sont possibles et il est important de les valider auprès des élèves, mais également de leur montrer que la dernière procédure, experte, est plus efficace : « Lors de la séance précédente, vous aviez compté le nombre de centaines isolées, puis le nombre de dizaines isolées et enfin les unités isolées. Ici, on va faire l'inverse : combien y a-t-il de centaines dans 453 ? »

Valider collectivement que le nombre de centaines est 4, car c'est le chiffre qui occupe le troisième rang à partir de la droite : « Puisqu'il y a 4 centaines, cela veut dire qu'il faut 4 plaques de 100 cubes. »

À l'aide de l'outil « Ardoise maths », projeter les quatre plaques au tableau. Procéder de la même façon pour représenter les dizaines et les unités.

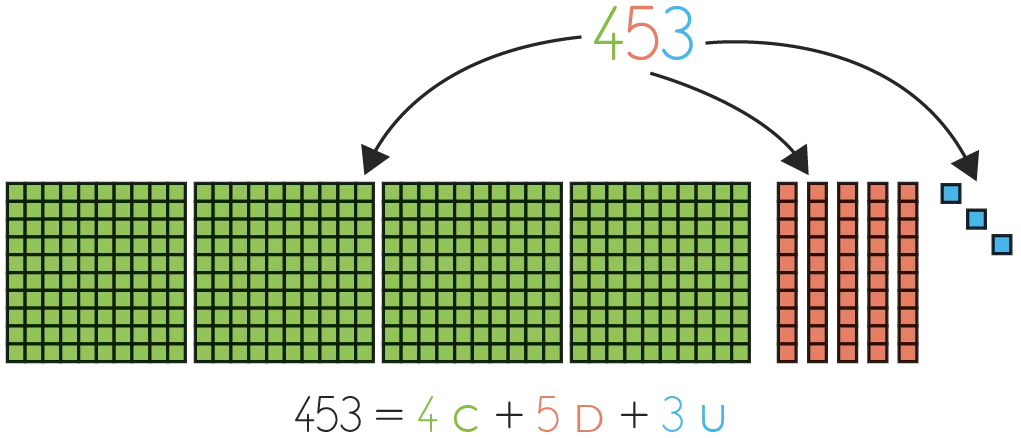
« Pour représenter 453, on l'a décomposé en centaines, dizaines et unités. C'est-à-dire qu'on l'a imaginé comme 4 centaines de cubes, 5 dizaines de cubes et 3 unités de cubes. »

Écrire la décomposition au tableau.

Faire représenter les nombres 237, 415 et 360 en laissant le matériel multibase à disposition.

Circuler pour encourager les élèves qui en ont besoin à utiliser la procédure experte proposée.

Corriger collectivement au tableau en procédant comme précédemment.

« Pour constituer une collection d'un nombre donné, on doit regarder le nombre de centaines, dizaines et unités isolées. On représente ensuite ces nombres avec le matériel multibase. Cette représentation en plaques de cent, barres de dix et cubes d'une unité peut aussi s'écrire avec des chiffres accompagnés de l'initiale de l'unité de numération correspondante. »

Compléter l'affiche de la séquence 1 en écrivant :

124 = 1 C + 2 D + 4 U

« Nous venons de voir une manière de représenter les nombres, mais ce n'est pas la seule. Dans la prochaine séance, nous en verrons d'autres. »

• Synthèse mathématique

« Qu'avez-vous appris durant cette séance ? »

Les élèves réfléchissent seuls, puis à deux.

Réponse attendue en revenant à la cible : décomposer un nombre en C, D et U pour construire la collection correspondante.

• Bilan de l'apprentissage

Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Maintenant, je sais que… »

L'élève réfléchit à son vécu de séance pour en livrer ce qui a été marquant pour lui dans son expérience d'élève, pas nécessairement dans le domaine mathématique.

Exemple : « Maintenant, je sais décomposer un nombre. »

Dénombrer une collection inférieure à 599

Projeter la carte rituel P1-5.

Demander aux élèves d'écrire les nombres en chiffres dans leur cahier de recherche.

Corriger devant les élèves et faire expliciter les réponses.

Variables didactiques

• Ne pas proposer que des formes prototypiques de type C, D et U, mais inverser en D, U et C ou U, D et C pour contourner les automatismes.
• Avoir plus de 10 dizaines ou unités.

Partie-tout : recherche d'une partie

Dans ma trousse, j'ai 20 crayons. 7 sont bleus, et les autres sont verts. Combien y a-t-il de crayons verts ?

Quelle situation correspond à l'énoncé ?

Projeter le problème intercalaire et les situations proposées. Échanger sur celle qui correspond à l'énoncé et en expliciter les raisons.

À l'aide de l'affiche, solliciter au moins deux élèves pour rappeler le contenu de la séance précédente.

« Aujourd'hui, nous allons continuer de construire des collections, mais cette fois, nous aurons des contraintes. »

Lire l'énoncé, puis le faire reformuler par les élèves pour s'assurer de sa bonne compréhension.

Laisser les élèves chercher pendant deux minutes. Faire le lien avec la séance précédente et le matériel multibase. Conclure en écrivant que le directeur doit acheter deux ramettes de 100 feuilles, un paquet de 10 feuilles et 3 feuilles seules, puis représenter, à l'aide de l'outil « Ardoise maths », la collection sous la forme 2 C, 1 D et 3 U.

Écrire au tableau : 1 C = … D = … U et 1 D = … U.

« Comment compléter ces égalités ? »

Réponse attendue : 1 C = 10 D = 100 U et 1 D = 10 U.

Présenter la situation-problème suivante comportant une contrainte sur les centaines.

Faire reformuler l'énoncé aux élèves, puis laisser les binômes réfléchir une minute avant de questionner : « Comment le directeur peut-il acheter 100 feuilles ? »

Laisser de nouveau les élèves chercher quelques minutes et circuler dans les rangs pour réexpliquer comment utiliser l'égalité entre 1 C et 10 D aux élèves qui en ont besoin. Il est nécessaire de laisser le matériel multibase accessible pour les binômes qui en éprouvent la nécessité.

Faire émerger l'idée qu'on peut acheter 10 ramettes de 10 feuilles pour avoir 100 feuilles. Entourer l'égalité au tableau.

Interroger au moins trois binômes pour qu'ils expliquent leur procédure. Certains élèves compteront de 10 en 10 pour chaque groupe de 100, voire jusqu'à 400. Il est important de mettre en évidence avec le matériel multibase qu'il est plus rapide de compter 10 dizaines de 1 en 1 plutôt que 100 de 10 en 10.

Montrer que 419 se décompose en 4 C, 1 D et 9 U. Or, 4 C = 40 D, c'est-à-dire que 419 se décompose également en 41 D et 9 U. On lit donc directement le nombre de dizaines et d'unités dans le nombre.

« Le directeur doit donc acheter 41 paquets de 10 feuilles et 9 feuilles individuelles pour commander 419 feuilles. »

« Pour représenter une collection, on peut utiliser différentes décompositions. Si on ne peut pas utiliser une des unités de numération pour représenter un nombre, comme ici les centaines, alors on peut utiliser les égalités que nous avons rappelées en début de séance ou lire directement le nombre de dizaines dans le nombre. »

Reprendre l'affiche de la séance 1 et la compléter avec une nouvelle décomposition : 124 = 12 D + 4 U.

Projeter les pages 14 et 15 du fichier et donner les consignes.

• Synthèse mathématique

« Qu'avez-vous appris durant cette séance ? »

Les élèves réfléchissent seuls, puis à deux.

Réponse attendue en revenant à la cible : décomposer un nombre pour construire une collection.

• Bilan de l'apprentissage

Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Pour réussir à construire une collection, je peux… »

Connaitre les compléments à 10
Projeter la carte rituel P1-6.
Demander aux élèves d'entourer les nombres dont les sommes sont égales à 10.
Corriger devant les élèves et faire expliciter les réponses.

Différenciation
Distribuer une autre grille aux élèves ayant terminé et faire barrer les sommes égales à 15.

Partie-tout : recherche d'une partie
Toumane a des billes. Il gagne 4 billes pendant la récréation. À la fin, il en a 9. Combien de billes avait-il avant ?

Quelle représentation correspond à l'énoncé ?
Projeter le problème intercalaire et les représentations proposées. Échanger sur celle qui correspond à l'énoncé et en expliciter les raisons.

« Qu'avons-nous vu lors de la séance précédente ? »
Laisser l'ensemble des élèves réfléchir une minute avant de recueillir au moins deux réponses.
Réponse attendue : construire et décomposer un nombre à partir des unités de numération.
« Aujourd'hui, nous allons apprendre à décomposer les nombres en faisant des additions. »

« Nous allons voir une autre manière d'écrire les nombres. Quels nombres entend-on dans "cinq-cent-trente-quatre" ? »
Réponse attendue : 500, 30, 4.

Les écrire au tableau au fur et à mesure et conclure en complétant l'écriture : « 534 est égal à 500 + 30 + 4. Cette écriture est une autre manière de décomposer les nombres : on appelle ça une "décomposition additive", parce qu'on utilise les additions. »

Faire le lien entre l'écriture précédente et la valeur de chaque unité de numération : 534 = 5 C + 3 D + 4 U = 500 + 30 + 4

« Pour écrire la décomposition additive d'un nombre, on peut s'aider de son nom ou lire la valeur de chaque chiffre. »

Modeler de nouveau en proposant un nombre dont la désignation orale n'est pas transparente : 286. Mettre en lumière qu'il faut connaitre la décomposition du 80 en « quatre fois vingt » pour décomposer ce nombre. Ce point permettra d'éviter les erreurs de type « 200 + 4 + 20 + 6 ».

Faire le lien de la même manière que pour 534 avec les unités de numération : 286 = 2 C + 8 D + 6 U = 200 + 80 + 6

Écrire 182, 372, 409 et 124 au tableau. « Décomposez les nombres suivants dans votre cahier de recherche, comme nous venons de le voir. Vous travaillez seul d'abord, puis vous pourrez passer en binômes. ». Circuler pour valider la procédure des élèves en réussite et aider ceux qui en ont besoin en décomposant les nombres avec eux.

« On peut décomposer un nombre en s'appuyant sur la place de chaque chiffre ou sur ce qu'on entend quand on le lit. On n'entend pas toujours directement le nom des chiffres qui composent un nombre, comme pour 286. La décomposition additive permet de savoir comment est construit un nombre. »

Compléter l'affiche de la séance 1 avec cette dernière décomposition.

Projeter la page 16 du fichier et donner les consignes.

• Synthèse mathématique
« Qu'avez-vous appris durant cette séance ? »
Les élèves réfléchissent seuls, puis à deux.
Réponse attendue en revenant à la cible : décomposer les nombres grâce à des additions.

• Bilan de l'apprentissage
Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Durant cette séance, j'ai aimé/je n'ai pas aimé… »