Résolution de problèmes
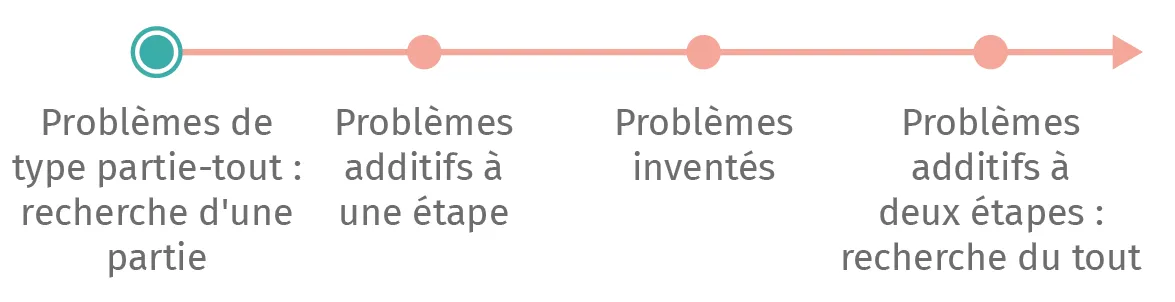
Problèmes de type partie-tout : recherche d'une partie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Trouver la valeur d'une partie à l'aide de l'autre partie déjà connue et du tout
- Résoudre des problèmes additifs en une étape
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les élèves renforcent leurs compétences pour reconnaître et résoudre des problèmes additifs simples à une étape, mobilisant addition ou soustraction, afin de développer la résolution de problèmes à étapes par la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Connaître les termes « partie », « tout » et « plus » dans des situations de calculs et de problèmes additifs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rappel des quatre étapes de résolution d'un problème : comprendre, modéliser, calculer et répondre.
(programmes publiés au BO du 31 octobre 2024)
Afin que les élèves soient de plus en plus à l'aise dans la résolution de problèmes, il est d'abord important de travailler avec eux une situation-problème de référence qui sera ensuite mis en mémoire et mobilisé pour résoudre de futures variations de ce type de problèmes « qui lui ressemblent ». En tant qu'adulte, il est possible de prendre conscience de l'importance de ce type de démarche par analogie en jouant à des jeux de logique. Par exemple, dans la question « Quelle lettre complète la suite logique : D – N – H – S – S – C – Q – ... ? », si la logique sous-jacente n'est pas maîtrisée, il est impossible de répondre de façon correcte. Par contre, si on sait que les lettres sont les initiales de chiffres dans l'ordre décroissant, on peut répondre « T » car c'est l'initiale de « trois ». Grâce à cette question de référence, on devient capable de trouver la réponse à toutes les questions répondant à la même logique. Pour dégager la logique sous-jacente d'un problème, les élèves peuvent s'appuyer sur des modélisations « en barre » qui permettent de rendre visuelle la situation mathématique en jeu.
Afin que les élèves soient de plus en plus à l'aise dans la résolution de problèmes, il est d'abord important de travailler avec eux une situation-problème de référence qui sera ensuite mis en mémoire et mobilisé pour résoudre de futures variations de ce type de problèmes « qui lui ressemblent ». En tant qu'adulte, il est possible de prendre conscience de l'importance de ce type de démarche par analogie en jouant à des jeux de logique. Par exemple, dans la question « Quelle lettre complète la suite logique : D – N – H – S – S – C – Q – ... ? », si la logique sous-jacente n'est pas maîtrisée, il est impossible de répondre de façon correcte. Par contre, si on sait que les lettres sont les initiales de chiffres dans l'ordre décroissant, on peut répondre « T » car c'est l'initiale de « trois ». Grâce à cette question de référence, on devient capable de trouver la réponse à toutes les questions répondant à la même logique. Pour dégager la logique sous-jacente d'un problème, les élèves peuvent s'appuyer sur des modélisations « en barre » qui permettent de rendre visuelle la situation mathématique en jeu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Séance 1
35 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectifs de la séance
- Comprendre et modéliser la recherche d'une partie à l'aide de l'autre partie déjà connue et du tout
- Installer une situation-problème de référence
Matériel de la séance
- Une grande affiche
- Cubes rouges et bleus
- Fichier élève p. 144
- Ressource numérique à projeter
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Lancement de la séance
Collectif
3 min
« Aujourd'hui, nous allons apprendre à résoudre des problèmes mathématiques dans lesquels on sait déjà combien il y a d'objets en tout. On cherche la valeur d'une partie. On connaît le nombre d'éléments de l'autre partie. »
Collectif
3 min


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Découverte de la situation-problème de référence
Collectif et binômes
6 min
Projeter l'animation « Problème de type partie-tout : recherche d'une partie ».Collectif et binômes
6 min
Situation-problème de référence
Une tour comporte 25 cubes bleus et des cubes rouges. Il y a 42 cubes en tout. Cherche combien il y a de cubes rouges dans la tour.
Laisser les élèves échanger à deux, puis interroger quelques binômes.
Exercice intercalaire
Que cherche-t-on ?
- 🟩 Combien de cubes bleus comprend la tour.
- 🔺 Le nombre de cubes rouges dans la tour.
- 🔵 La quantité totale de cubes dans la tour.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Phase de recherche
Individuel et binômes
8 min
Projeter la page 144 du fichier et donner les consignes.Individuel et binômes
8 min
« Vous allez chercher seuls la réponse à la question. Vous pouvez prendre du matériel et dessiner pour vous aider si vous le souhaitez. Lorsque vous pensez avoir trouvé, vous écrivez la réponse dans votre fichier, puis vous vous mettrez d'accord avec votre voisin sur la réponse. Vous pourrez modifier ce que vous aviez écrit si vous le voulez. »
Différenciation
Élèves éprouvant des difficultés
Certains élèves n'auront pas besoin de passer par la schématisation ; il n'est pas utile de la leur imposer. Si des élèves ont terminé avant la fin du temps imparti, ils peuvent essayer de résoudre un problème issu de la banque de problèmes accessible sur l'espace numérique ou sur .
- Proposer de choisir, parmi trois représentations, celle qui correspond à la situation.
- Proposer du matériel tangible plus ou moins figuratif et constituer les collections en jeu avec eux.
- Passer par une représentation dessinée ou schématisée pour constituer les collections en jeu avec eux.
- Les accompagner en verbalisant et en représentant successivement et progressivement les différentes étapes : « On dessine 4 paquets de 10 cubes et 2 cubes isolés. On colorie 2 paquets de 10 et 5 cubes seuls en bleu. On colorie le reste en rouge : il y en a 17. »
Certains élèves n'auront pas besoin de passer par la schématisation ; il n'est pas utile de la leur imposer. Si des élèves ont terminé avant la fin du temps imparti, ils peuvent essayer de résoudre un problème issu de la banque de problèmes accessible sur l'espace numérique ou sur .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Mise en commun
Collectif
5 min
Recueillir quelques productions d'élèves et les reformuler si besoin.Collectif
5 min
L'objectif est d'observer différentes représentations proposées par les élèves et de leur demander d'expliquer leur méthodologie de résolution. Pour chaque proposition, demander au groupe-classe : « Est-ce que cette réponse est possible ? » afin de les faire réfléchir à la vraisemblance du résultat proposé. Si un élève propose 67 (en calculant 25 + 42), alors lui faire remarquer que l'on cherche le nombre de cubes rouges, qui est forcément inférieur au nombre total de cubes dans la tour.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Institutionnalisation
Collectif
8 min
Accrocher au tableau une affiche sur laquelle est écrit la situation-problème de référence, puis indiquer : « Nous allons faire une affiche pour nous souvenir de ce problème. Nous avions 42 cubes en tout. » Dessiner de façon schématique un bloc horizontal représentant l'ensemble des cubes et écrire « 42 en tout » à l'intérieur.
Collectif
8 min
« 25 étaient bleus. » Dessiner un autre bloc rectangulaire sous le premier et écrire « 25 bleus » à l'intérieur.
« Nous cherchions combien il manque pour aller de 25 à 42. » Dessiner un troisième bloc rectangulaire sous le premier et à droite du deuxième et écrire « ? rouges » à l'intérieur.
Procéder à la résolution du problème en aboutissant à une modélisation de type « barre » permettant de visualiser la situation mathématique en jeu.


« Nous avons trouvé qu'il y a 17 cubes rouges dans la tour. »



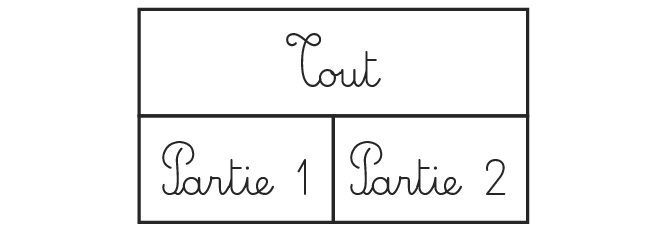
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Bilan
En binômes et individuel
5 min
En binômes et individuel
5 min
- Synthèse mathématique « Qu'avez-vous appris durant cette séance ? »
- Bilan de l'apprentissage Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Pour réussir à résoudre ce type de problème, je dois... »
Les élèves réfléchissent seuls, puis à deux.
Réponse attendue en revenant à la cible : résoudre des problèmes de recherche de la valeur d'une partie d'un tout.
Projeter la page 144 du fichier et donner les consignes du problème intercalaire.


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

