Calcul
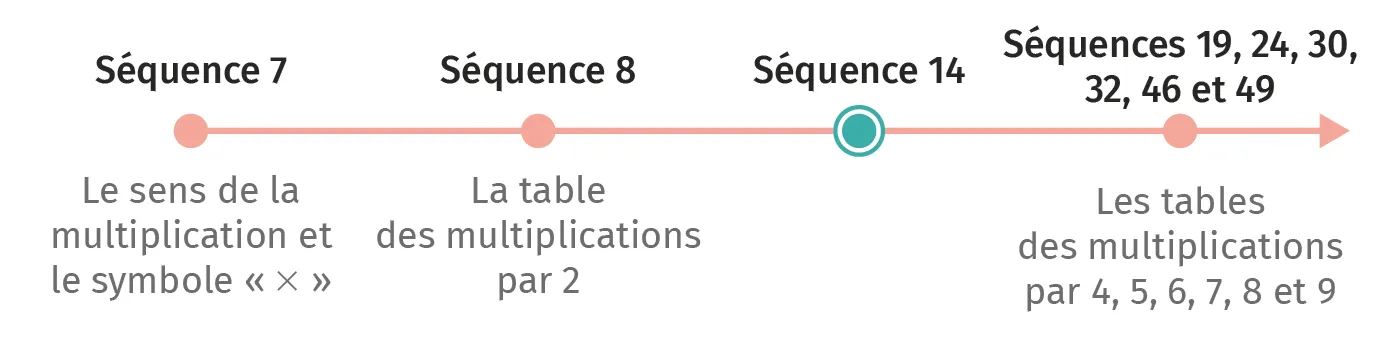
Séquence 14
La table des multiplications par 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Construire la table des multiplications par 3
- Connaître dans les deux sens les résultats de la table des multiplications par 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La connaissance de faits
numériques permet aux élèves
de développer des stratégies
de calcul et de mieux réussir
en résolution de problèmes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Comprendre le sens de la multiplication
- Représenter une multiplication en configuration rectangulaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'apprentissage des tables de multiplication se fait sur le long terme. L'appui sur la configuration rectangulaire répond à une montée en abstraction permettant aux élèves de visualiser les produits, avant de passer à l'écriture chiffrée représentée dans la table de Pythagore et les tables en colonnes. Cette représentation rectangulaire permet également de mettre la commutativité en lumière et constitue un support de choix pour aborder la distributivité. La ritualisation n'est pas à confondre avec la répétition des modalités : les tables sont travaillées à partir des mêmes supports, mais le sens des opérations varie afin de favoriser la pleine maîtrise de ces faits numériques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Séance 1
65 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Comparer avec < ou >
Projeter et distribuer la carte rituel P2-6. Demander aux élèves de compléter par < ou >.
Corriger devant les élèves et faire expliciter les réponses.Variable didactique
Demander aux élèves de se chronométrer.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie-tout : recherche d'une partie
Un bijoutier propose 56 bijoux en vitrine dont 35 sont des colliers, et le reste des bracelets. Combien peut-on acheter de bracelets ?Problème résolu : quelle démarche a été utilisée ?
Projeter le problème intercalaire et les démarches de résolution proposées. Échanger sur celle qui correspond au problème résolu et en expliciter les raisons.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectifs de la séance
- Construire la table des multiplications par 3
- Connaître dans les deux sens les résultats de la table des multiplications par 3
Matériel de la séance
- Une étiquette « produit » par binôme, à imprimer
- Une feuille à carreaux par binôme
- La table de Pythagore rectangulaire individuelle, débutée en séquence 8
- Un dé à six faces numérotées de 1 à 3 et un dé à dix faces par binôme
- Fichier élève
- Ressource numérique à projeter
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Lancement de la séance
Collectif
3 min
Afin de rappeler le sens de la multiplication et de la commutativité, faire réfléchir l'ensemble de la classe durant une minute, puis solliciter au moins deux élèves pour l'expliciter.Collectif
3 min


Projeter l'outil « Table de Pythagore » pour montrer les tables déjà connues et celles restant à apprendre. « Vous connaissez déjà le début de la table des multiplications par 3. Aujourd'hui, vous allez apprendre à calculer la suite. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Pratique en binômes
En binômes
6 min
Distribuer une étiquette « produit » et une feuille à carreaux à chaque binôme. « Dessinez un rectangle correspondant à la multiplication qui se trouve sur votre étiquette. Par exemple, pour 2 × 3, je dessine un rectangle de deux carreaux pour le premier côté et de trois carreaux pour le second côté, puis je dessine les deux autres côtés. »En binômes
6 min
Les élèves dessinent le rectangle correspondant à leur multiplication sur leur feuille et le découpent, puis écrivent le calcul et son résultat à l'intérieur. Ils vérifient ensuite le travail d'un autre binôme.
Circuler pour valider la procédure des élèves en réussite et aider ceux qui en ont besoin en reprenant la construction des rectangles et le lien avec la multiplication associée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Mise en commun
Collectif
8 min
Travailler à partir des rectangles construits par les élèves ou
projeter l'outil « Table de Pythagore ».Collectif
8 min
Faire énoncer le nombre de carreaux des rectangles de chaque binôme afin de rassembler ceux qui ont le même nombre. Montrer la commutativité en tournant les rectangles. Faire ranger les rectangles du plus petit au plus grand.
Les élèves ont construit la table des multiplications par 3.
« Le premier rectangle, 3 × 1, est égal à 3, car on dénombre bien trois carreaux à l'intérieur. Le deuxième rectangle, 3 × 2, est égal à 6, car on dénombre bien six carreaux à l'intérieur. » Verbaliser ainsi jusqu'à 3 × 10. Faire dire les résultats de la table dans les deux sens : « 3 × 2 égale 6 et 6 égale 3 × 2 et aussi 2 × 3. »
Grâce à l'outil « Table de Pythagore », mettre en évidence que les résultats vont de 3 en 3, en l'expliquant grâce aux rectangles qui contiennent à chaque fois trois carreaux de plus.
Le travail doit aboutir à une représentation de ce type.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Institutionnalisation
Collectif
5 min
Projeter l'outil « Table de Pythagore », puis le remplir avec les résultats de la table des multiplications par 3. Les élèves font de même sur leur table de Pythagore rectangulaire individuelle. Faire dire la table à l'endroit et à l'envers au groupe-classe.
Collectif
5 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Pratique guidée
En binômes
10 min
En binômes
10 min
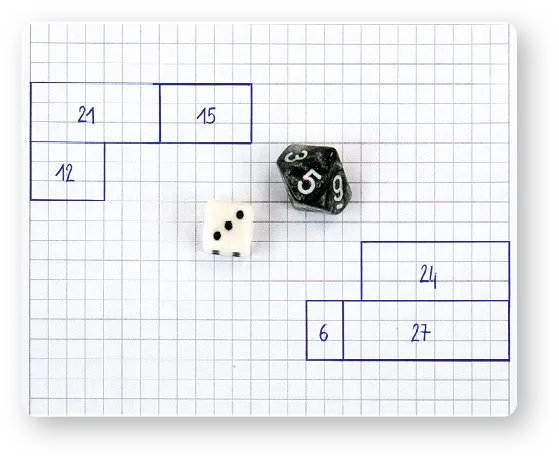
Jeu du nombre rectangle
Préparer les dés : un dé à dix faces numérotées de 0 à 9 et un dé à six faces ne faisant apparaître que 1, 2 et 3 par binôme. « Chaque binôme aura deux dés. Le premier joueur lance les dés. Il dessine le rectangle correspondant sur la feuille, puis écrit le calcul et son résultat à l'intérieur. Le second joueur lance les dés à son tour et fait la même chose. À chaque nouveau tour, les joueurs dessinent un nouveau rectangle, collé à ceux des tours précédents. À la fin de la partie, les joueurs additionnent les résultats des tables, c'est-à-dire leur nombre total de carreaux. Celui qui a le plus de carreaux a gagné. » Circuler pour valider les procédures des élèves en réussite et aider ceux qui en ont besoin.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le jeu du nombre rectangle est utilisé à chaque séance de construction des tables, en ajoutant la nouvelle table vue lors de la séance concernée, ce qui favorise leur mémorisation. Il est possible d'envisager une version inversée en donnant aux élèves le support d'une partie déjà réalisée sur une feuille blanche. Ils n'ont ainsi pas la possibilité de compter les carreaux et doivent écrire la multiplication associée dans les rectangles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Entraînement sur fichier (pratique autonome)
Individuel
8 min
Projeter la du fichier et donner les consignes.
Individuel
8 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Bilan
En binômes et individuel
5 min
En binômes et individuel
5 min
- Synthèse mathématique « Qu'avez-vous appris durant cette séance ? »
- Bilan de l'apprentissage Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Pour mémoriser les résultats de la table des multiplications par 3, je dois... »
Les élèves réfléchissent seuls, puis à deux.
Réponse attendue en revenant à la cible : les résultats de la table des multiplications par 3 dans les deux sens.


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

