Espace et géométrie

1. On souhaite construire un triangle pour lequel la somme des mesures des angles est la plus grande possible.

a. Construire plusieurs triangles pour tenter de répondre au problème et mesurer la somme des mesures des angles des triangles ainsi construits.

b. Qu'observe-t-on ?

2. On donne ci-dessous trois triangles.


a. Justifier que ces triangles sont égaux, puis repérer en rouge sur les triangles \mathrm{CDE} et \mathrm{FGH} les angles égaux à \mathrm{\widehat{A}}, en vert les angles égaux à \mathrm{\widehat{B}} et en noir les angles égaux à \mathrm{\widehat{C}}.

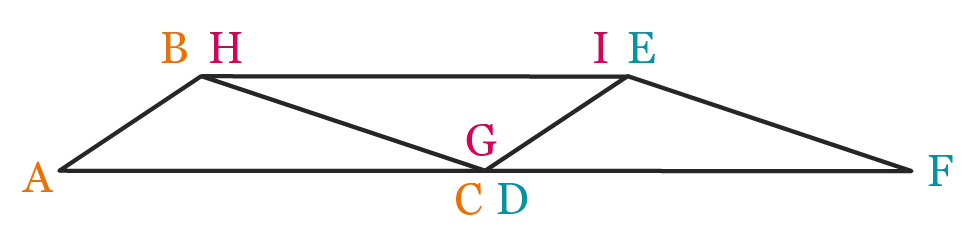
b. Observer la construction ci-dessous. Que peut-on dire sur la somme des mesures des angles d'un triangle ?

Dans la figure ci-dessous, on a placé cinq points \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D} et \mathrm{E} et on a tracé les symétriques de ces points \mathrm{A'}, \mathrm{B'}, \mathrm{C'}, \mathrm{D'} et \mathrm{E'} par rapport à la droite (d).

1. Définition de la symétrie axiale.

a. Tracer en vert les segments \text { [} \left.\mathrm{AA}^{\prime}\right],\left[\mathrm{BB}^{\prime}\right],\left[\mathrm{CC}^{\prime}\right],\left[\mathrm{DD}^{\prime}\right] et \left[\mathrm{EE}^{\prime}\right].
b. À quoi correspond la droite (d) pour ces segments ?

2. Étude de la conservation des longueurs par symétrie axiale.

a. Tracer en bleu les segments [\mathrm{AE}] et [\mathrm{A'E'}].

b. Justifier que les segments [\mathrm{AE}] et [\mathrm{A'E'}] sont symétriques par rapport à la droite (d).

c. À l'aide d'un compas, comparer les longueurs \mathrm{AE} et \mathrm{A'E'}.

d. Reprendre les questions précédentes avec les segments [\mathrm{DC}] et [\mathrm{D'C'}].

3. Étude de la conservation des mesures d'angle par symétrie axiale.

a. Mesurer les angles \widehat{\mathrm{ABC}} et \widehat{\mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}}. Que peut-on observer ?

b. Reprendre la question précédente avec les angles \widehat{\mathrm{AEC}} et \widehat{\mathrm{A}^{\prime} \mathrm{E}^{\prime} \mathrm{C}^{\prime}}.