Thème 3 : Espace et géométrie
Fiche 42
Tracer, reconnaître et utiliser la médiatrice d'un segment
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définition
La médiatrice d'un segment est la droite perpendiculaire à ce segment passant par son milieu.
Propriété
La médiatrice d'un segment est un axe de symétrie de ce segment.

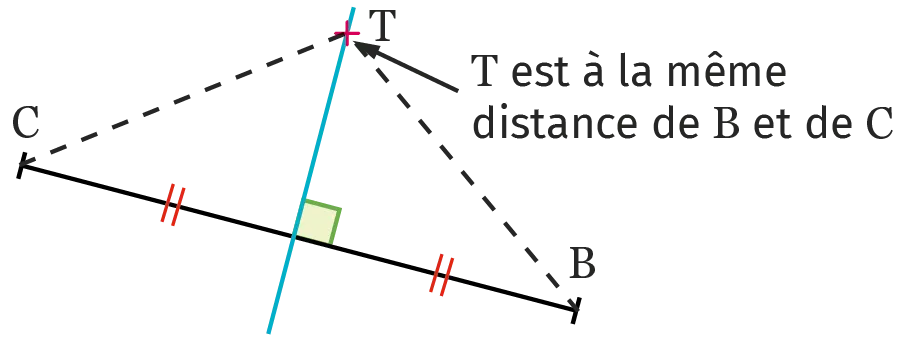
Propriété
Tous les points qui appartiennent à la médiatrice d'un segment sont équidistants des extrémités de ce segment, et réciproquement.
- Remarque : Si \mathrm{T} est sur la médiatrice de [\mathrm{BC}], alors le triangle \mathrm{BCT} est isocèle en \mathrm{T}.
Méthode
Construire la médiatrice d'un segment [\mathrm{AB}] avec le compas et la règle non graduée.
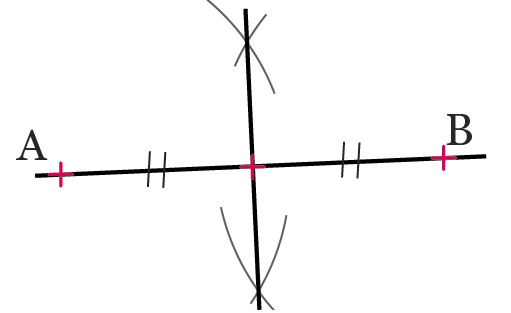
1. Pointer le compas sur le point \mathrm{A} avec un écartement supérieur à la moitié de \mathrm{AB}. Tracer ensuite un arc de cercle de part et d'autre du segment.




2. En conservant la même ouverture de compas, pointer le compas sur le point \mathrm{B}, puis tracer un deuxième arc de cercle de chaque côté du segment.




3. Tracer la droite passant par l'intersection des arcs de cercle : c'est la médiatrice de [\mathrm{AB}]. Coder la figure.



Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le problème de Napoléon consiste à construire
uniquement à l'aide d'un compas le centre
d'un cercle donné. Si on s'autorise une version
plus simple utilisant également la règle
non graduée, les médiatrices permettent de
répondre facilement au problème.
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

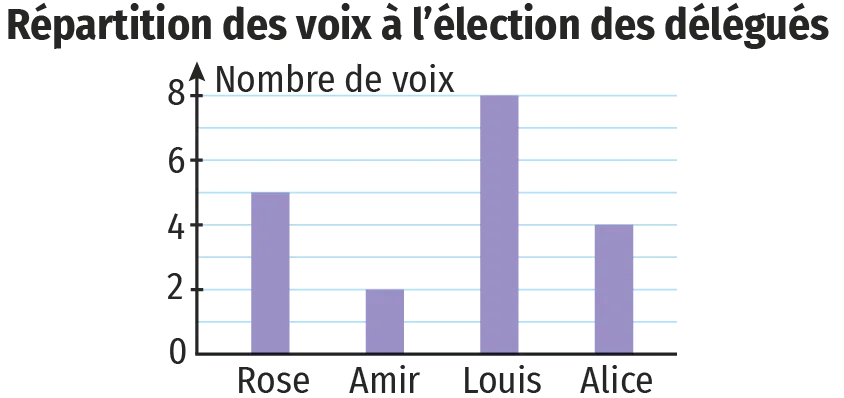
1. Qui a obtenu le plus de voix ?
2. Combien de personnes ont voté ?
3. Combien de personnes ont obtenu au moins 4 voix ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Entourer la figure sur laquelle la droite (d) est la médiatrice du segment [\mathrm{AB}].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Construire à l'aide de la règle graduée et de l'équerre la médiatrice des segments [\mathrm{MN}] et [\mathrm{PB}].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Construire à l'aide de la règle non graduée et du compas les médiatrices des segments [\mathrm{AC}] et [\mathrm{RS}].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Relier chaque phrase avec le(s) objet(s) géométrique(s) correspondant(s).

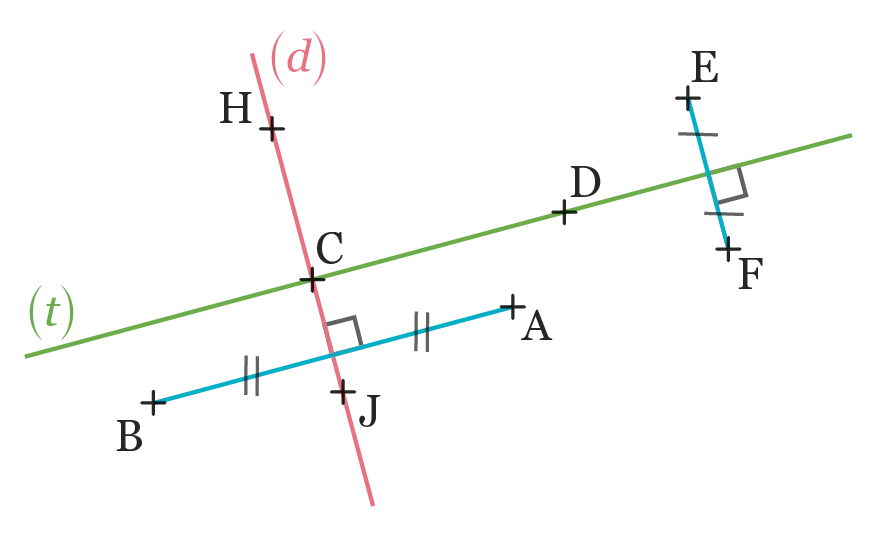


- Je suis équidistant de \mathrm{B} et \mathrm{A}.
- Je suis à la même distance de \mathrm{E} et \mathrm{F}.
- Je suis un axe de symétrie de [\mathrm{EF}].
- Je suis la médiatrice de [\mathrm{AB}].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Agnès (\mathrm{A}) et Bilal (\mathrm{B}) se sont donné rendez-vous sur le chemin et ils veulent parcourir la même distance pour se rejoindre.
Placer tous les points de rendez-vous possibles.
Placer tous les points de rendez-vous possibles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
On donne la figure ci-dessous.
1. a. Construire à la règle non graduée et au compas la médiatrice (d) du segment [\mathrm{AB}].
b. Placer un point \mathrm{D} sur (d). Que peut-on dire du triangle \mathrm{ABD} ?
2. Construire le point \mathrm{E} tel que \mathrm{ABE} et \mathrm{BCE} sont isocèles en \mathrm{E}.
1. a. Construire à la règle non graduée et au compas la médiatrice (d) du segment [\mathrm{AB}].
b. Placer un point \mathrm{D} sur (d). Que peut-on dire du triangle \mathrm{ABD} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Énigme
Déterminer le centre du cercle à l'aide d'un compas et d'une règle non graduée.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

