Thème 3 : Espace et géométrie
Fiche 41
Utiliser les propriétés angulaires des triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouver une activité de découverte .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Propriétés
1. Si un triangle a deux angles de même mesure, alors il est isocèle. Réciproquement, dans un triangle isocèle, les angles adjacents à la base sont de même mesure.
2. Si un triangle a ses trois angles de même mesure, alors il est équilatéral. Réciproquement, tout triangle équilatéral a ses trois angles de même mesure.
Propriété
La somme des mesures des trois angles d'un triangle est toujours égale à 180°.
- Remarque : Dans un triangle équilatéral, chaque angle mesure 60°.
Supplément numérique
Retrouver une .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La somme des mesures des quatre angles d'un
trapèze vaut 360°.
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Le périmètre d'un carré de côté 8~\mathrm{cm} :
2. 32~\mathrm{cm} = \mathrm{m}
3. \frac{1}{2} =
2. 32~\mathrm{cm} =
3. \frac{1}{2} =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
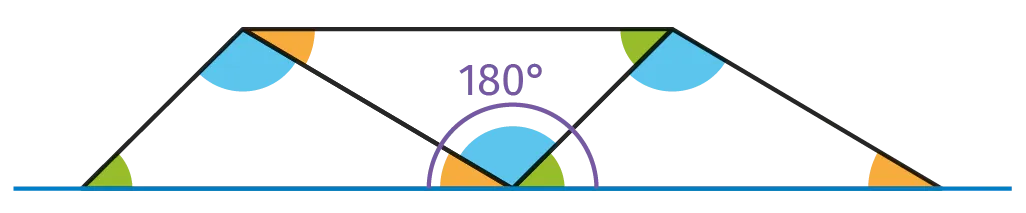
1. Quelle propriété du cours est illustrée par cette figure ?



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Compléter le raisonnement pour justifier que les trois angles d'un triangle équilatéral \mathrm{ABC} mesurent chacun 60°.
Le triangle équilatéral \mathrm{ABC} est en particulier isocèle en donc = .
De plus, le triangle \mathrm{ABC} est également isocèle en donc = .
Ainsi, = = .
Or la somme des mesures des angles d'un triangle vaut donc chaque angle mesure \div = .
Le triangle équilatéral \mathrm{ABC} est en particulier isocèle en
De plus, le triangle \mathrm{ABC} est également isocèle en
Ainsi,
Or la somme des mesures des angles d'un triangle vaut
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
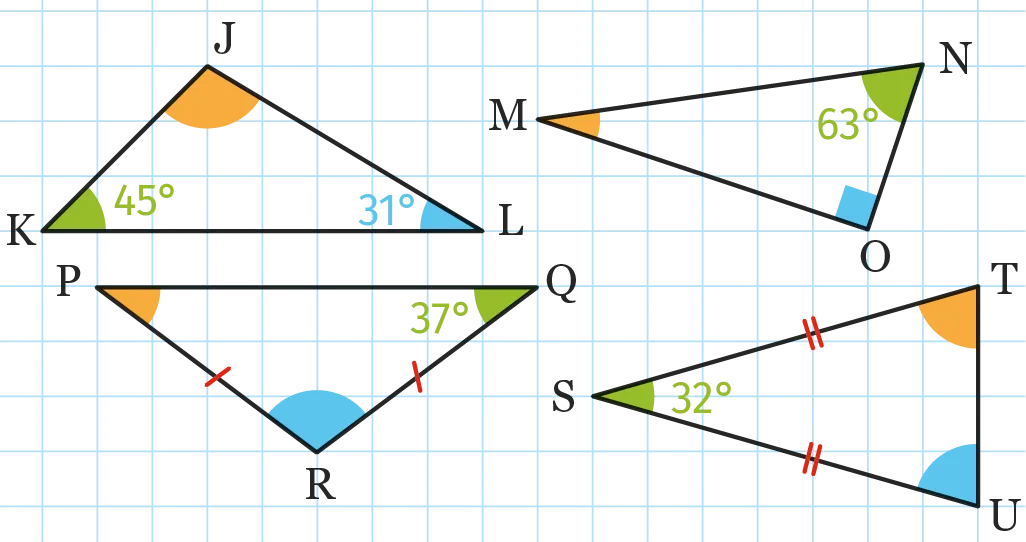
Dans chaque cas, déterminer les mesures des angles manquantes.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Construire le triangle \mathrm{ABC} isocèle en \mathrm{A} tel que \mathrm{BC} = 5~\mathrm{cm} et \widehat{\mathrm{BAC}} = 40°.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Construire le triangle \mathrm{DEF} isocèle en \mathrm{F} tel que \mathrm{DE} = 4~\mathrm{cm} et \widehat{\mathrm{DEF}} = 40°.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Construire, en vraie grandeur, la figure suivante, puis déterminer en justifiant si les points \mathrm{E}, \mathrm{F} et \mathrm{I} sont alignés.

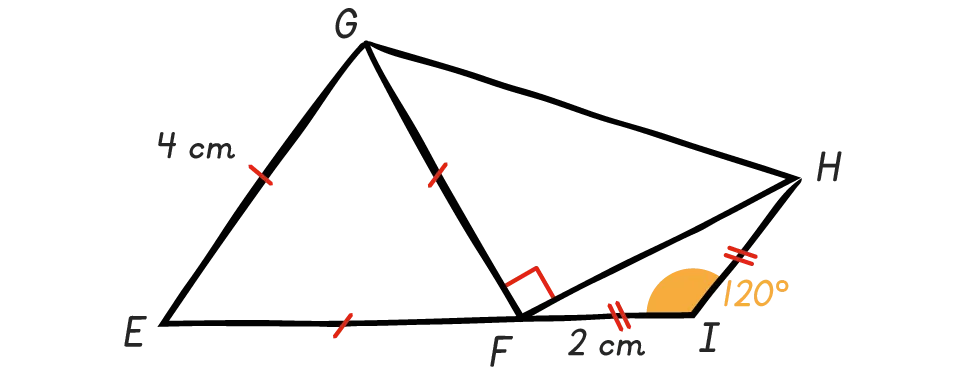
Coup de pouce
Si \widehat{\mathrm{EFI}} = 180°, alors \mathrm{E}, \mathrm{F} et \mathrm{I} sont alignés.


Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
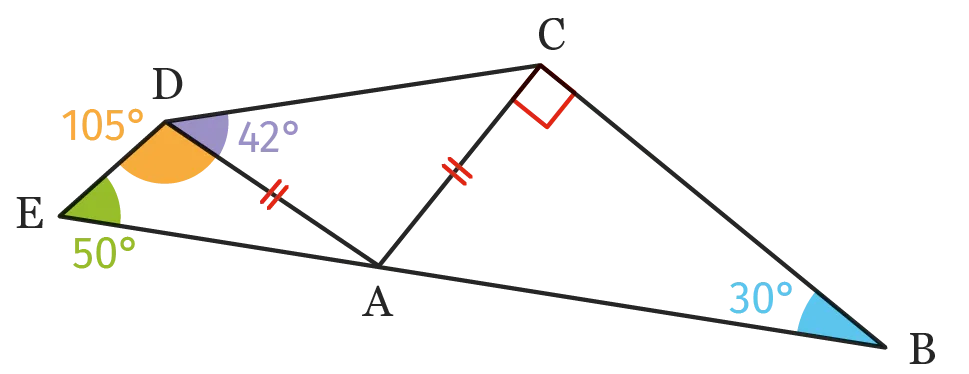
Déterminer si les points \mathrm{E}, \mathrm{A} et \mathrm{B} sont alignés.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Énigme
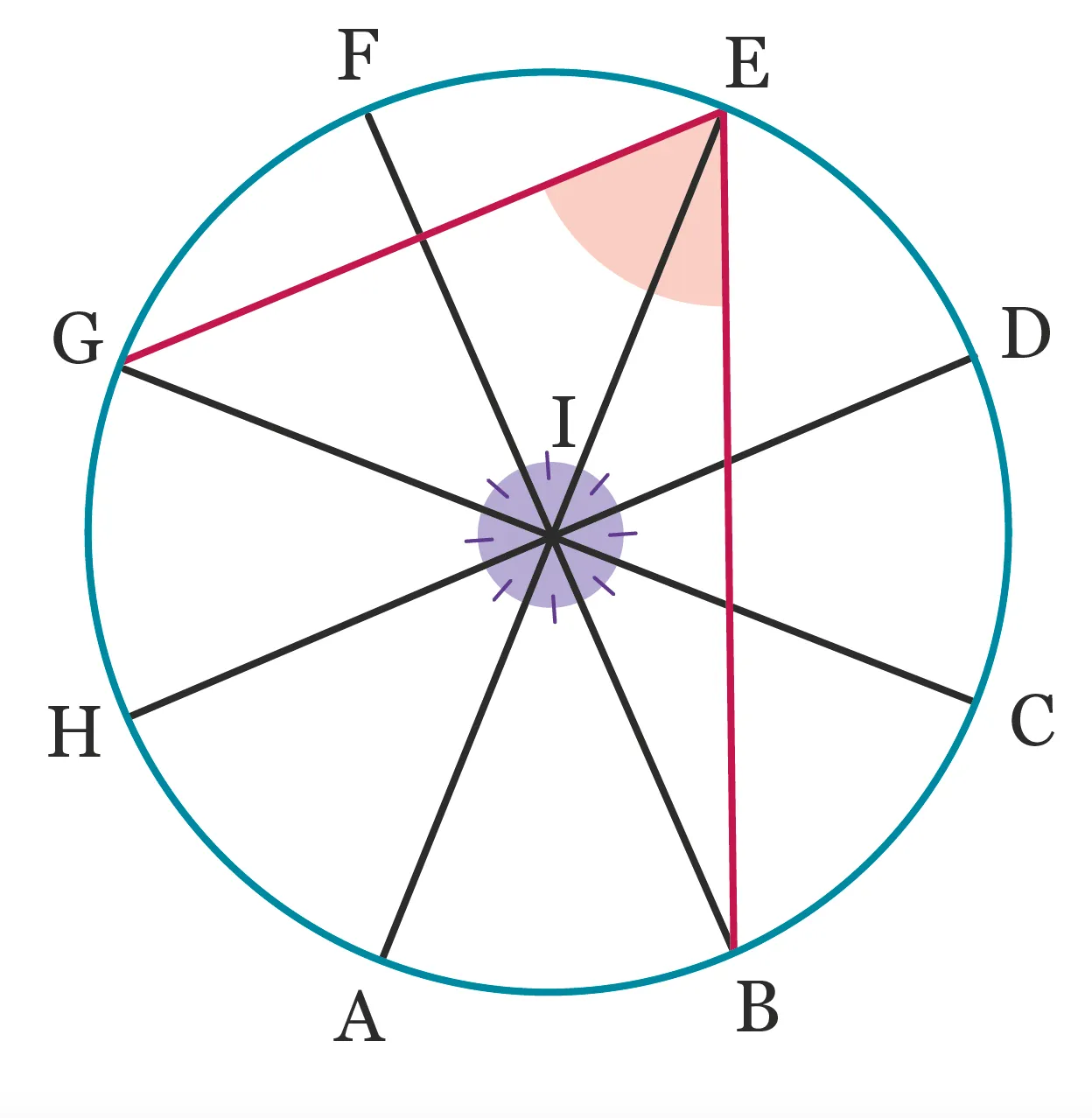
Les points \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{F}, \mathrm{G} et \mathrm{H} sont sur le cercle de centre \mathrm{I} ci-dessous. En utilisant les informations de la figure, déterminer la mesure de l'angle \widehat{\mathrm{GEB}}.



Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

