Thème 3 : Espace et géométrie
Fiche 40
Construire un triangle (2)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Propriétés
Un triangle peut être entièrement défini par :
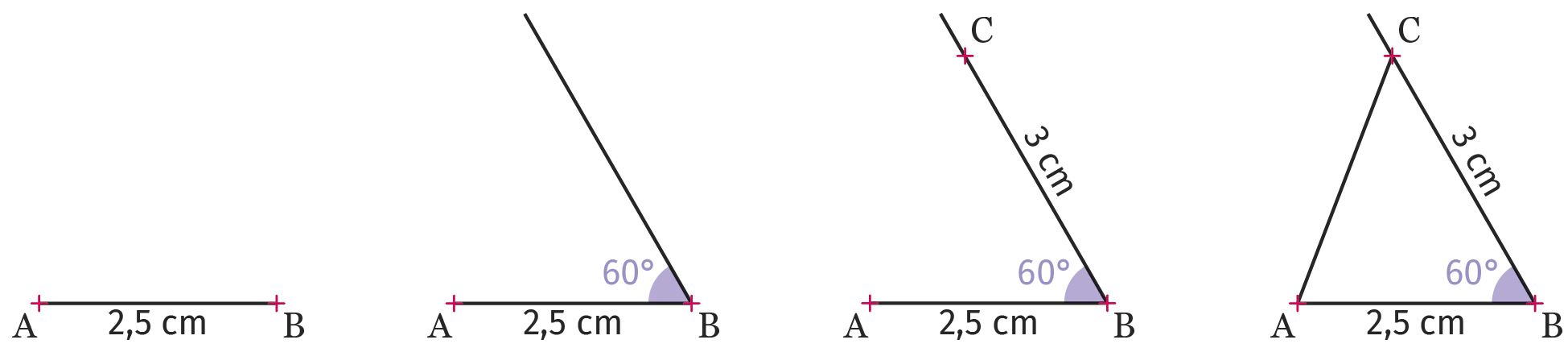
- les longueurs de deux de ses côtés et la mesure de l'angle délimité par ces côtés.
Exemple : On peut construire le triangle \mathrm{ABC} tel que \mathrm{AB} = 2,5~ \mathrm{cm}, \mathrm{BC} = 3~ \mathrm{cm} et \mathrm{ABC} = 60°.
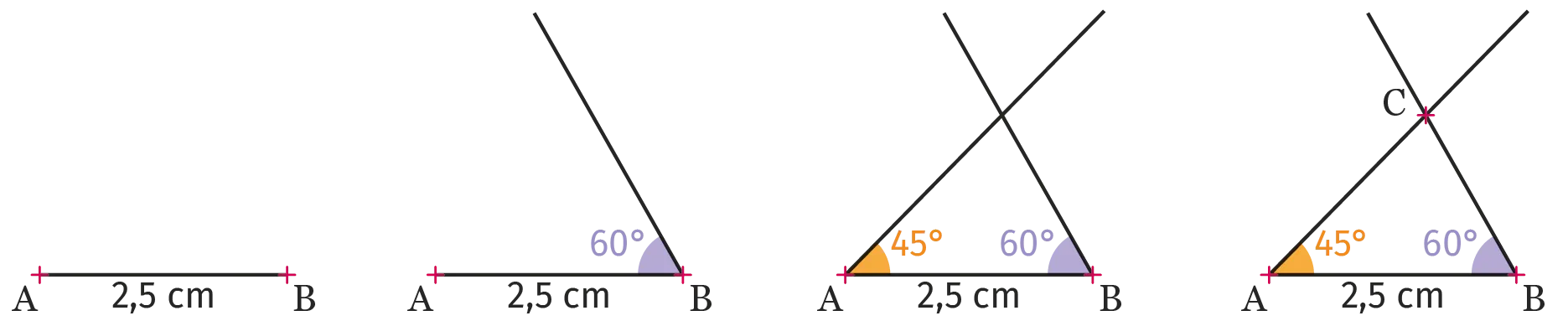
- la longueur d'un seul côté et les mesures des angles adjacents à ce côté.
Exemple : On peut construire le triangle \mathrm{ABC} tel que \mathrm{AB} = 2,5~ \mathrm{cm}, \mathrm{\widehat{ABC}} = 60° et \mathrm{\widehat{CAB}} = 45°.
Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La construction d'un triangle à partir de la
longueur d'un seul côté et des mesures de ses
angles adjacents est la base de la méthode de
triangulation, très utilisée pour déterminer des
distances difficilement mesurables (distance à
la côte d'un bateau en mer, etc.).
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Trois fois moins que 15 :
2. Quelle heure indique l'horloge ?
2. Quelle heure indique l'horloge ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Construire le triangle \mathrm{TIK}, rectangle en \mathrm{I}, tel que \mathrm{IK} = 3~\mathrm{cm} et \mathrm{IT} = 7~\mathrm{cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Construire le triangle \mathrm{CAT} tel que \mathrm{AC} = 8~\mathrm{cm}, \mathrm{AT} = 6~\mathrm{cm} et \widehat{\mathrm{CAT}} = 60°.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Construire le triangle \mathrm{DOG} tel que \mathrm{DG} = 3~\mathrm{cm}, \widehat{\mathrm{ODG}} = 30° et \widehat{\mathrm{DGO}} = 110°.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Construire le triangle \mathrm{TOK}, rectangle en \mathrm{O}, tel que \mathrm{OK} = 4~\mathrm{cm} et \mathrm{\widehat{TKO}} = 40°.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Reproduire la figure ci-dessous en respectant les codages indiqués.

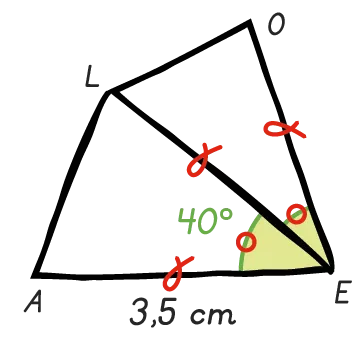


Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Sacha affirme à tort qu'un triangle est entièrement défini par ses mesures d'angle. Donner un contre-exemple en construisant deux triangles de longueurs différentes et dont les mesures d'angles sont 90°, 60° et 30°.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Énigme
Dans le pentagone régulier ci-dessous, \mathrm{DEL} est un triangle d'argent, c'est-à-dire un triangle isocèle dont les angles adjacents à la base mesurent 36°.

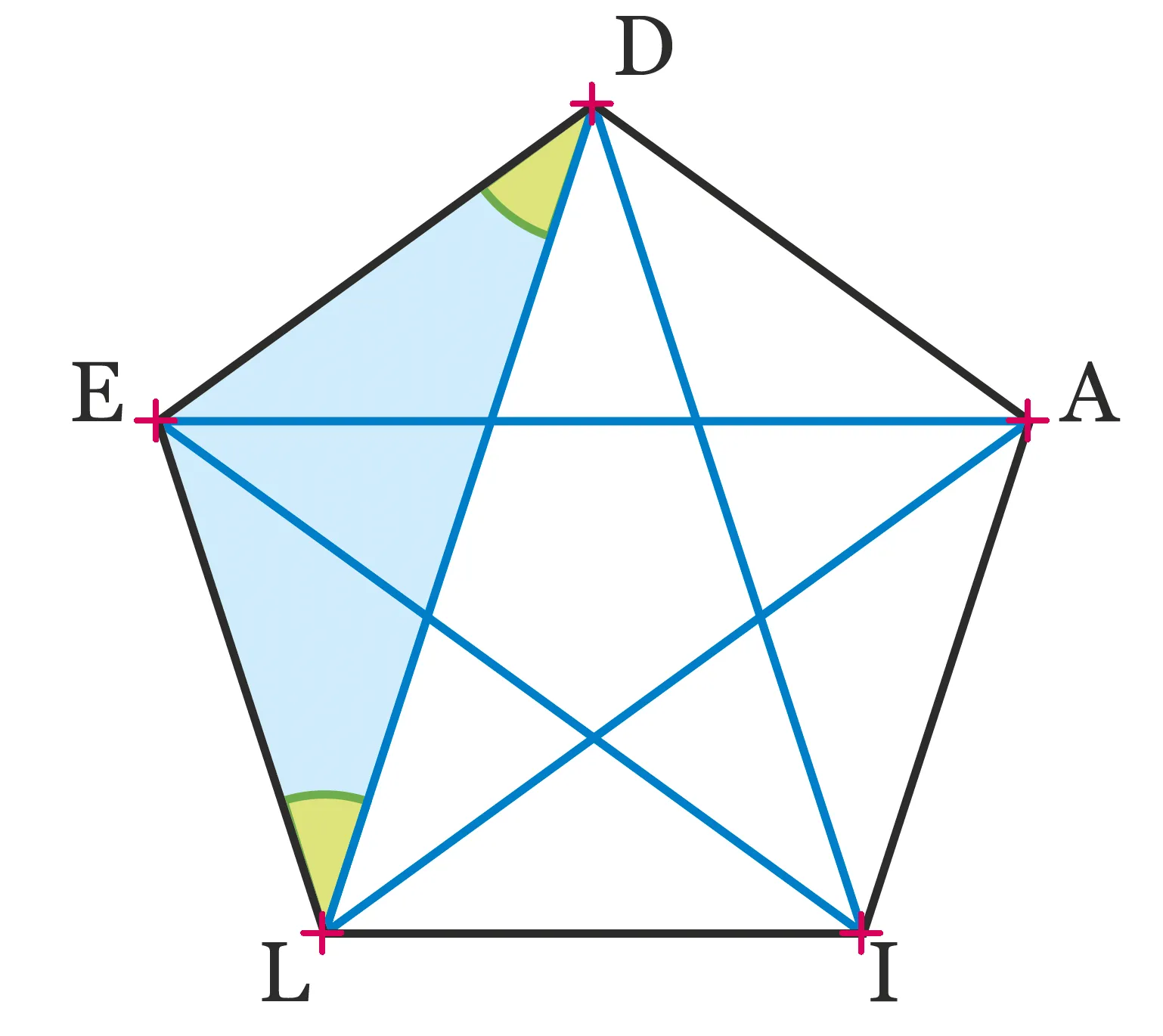
Combien compte-t-on de triangles d'argent dessinés à l'intérieur du pentagone \mathrm{ADELI} ?


Combien compte-t-on de triangles d'argent dessinés à l'intérieur du pentagone \mathrm{ADELI} ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille



