Thème 3 : Espace et géométrie
Fiche 39
Construire un triangle (1)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Définitions
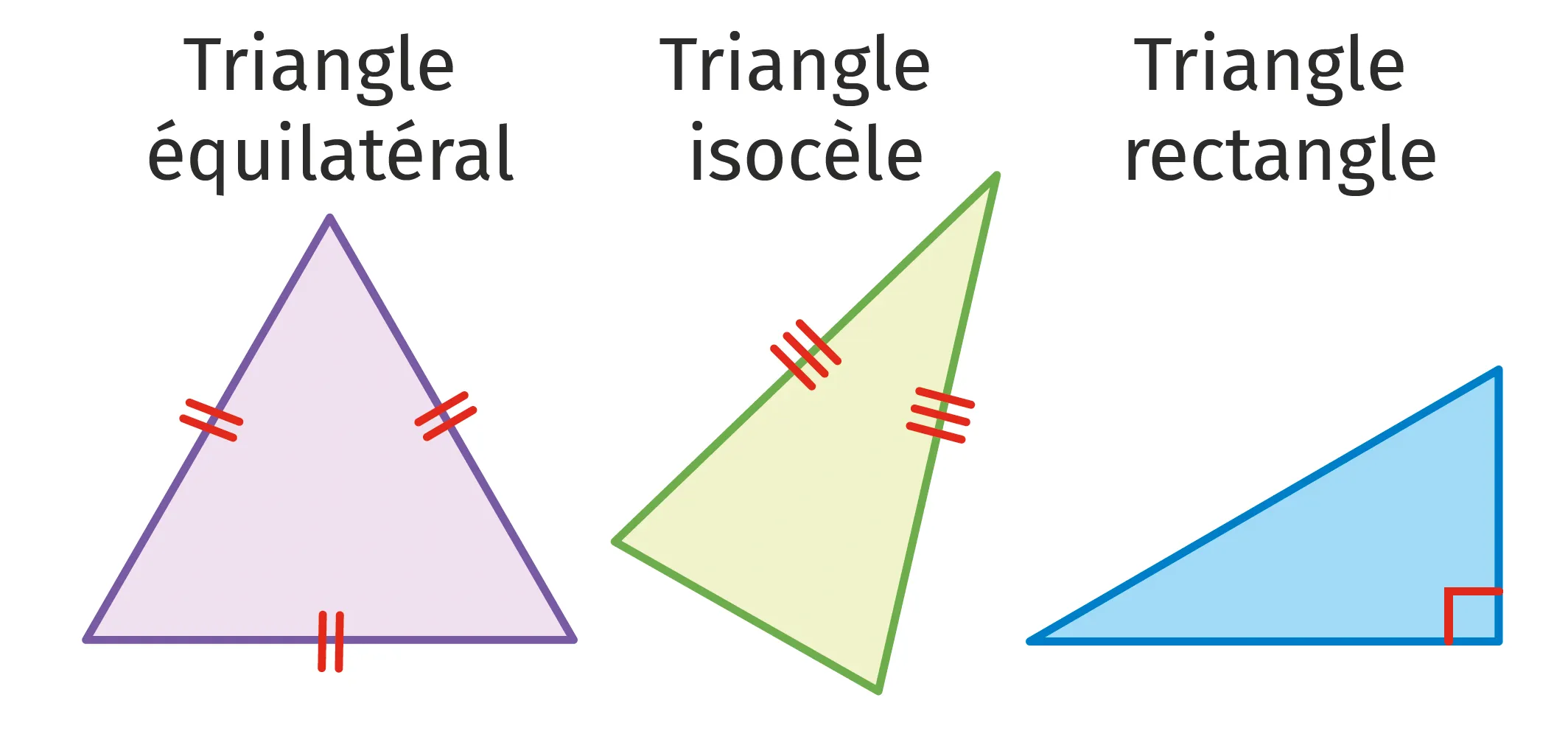
- Un triangle est équilatéral lorsque ses trois côtés ont la même mesure.
- Un triangle est isocèle lorsque deux de ses côtés ont la même mesure.
- Un triangle est rectangle lorsqu'il possède un angle droit.

Propriété
Un triangle est entièrement défini par la donnée des trois longueurs de ses côtés.
En connaissant les longueurs des trois côtés d'un triangle, on peut le construire en utilisant la règle graduée et le compas.
- Remarque : Pour qu'un triangle soit constructible, il faut que la longueur du plus grand côté soit inférieure ou égale à la somme des longueurs des deux autres côtés.
Supplément numérique
Cette notion en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un triangle ayant trois longueurs différentes est
appelé un triangle scalène, qui signifie en grec
« oblique » ou « boiteux ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. 0,01~ \mathrm{m} = \text{mm}
2. Une année bissextile : jours
3. \frac{1}{2} + \frac{1}{2} =
4. 1 - \frac{1}{4} =
2. Une année bissextile :
3. \frac{1}{2} + \frac{1}{2} =
4. 1 - \frac{1}{4} =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
1. Construire le triangle \mathrm{DEF} tel que \mathrm{DE}=6,5~\mathrm{cm}, \mathrm{DF}=5~\mathrm{cm} et \mathrm{EF}=4~\mathrm{cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Construire le triangle \mathrm{RST} isocèle en \mathrm{T} vérifiant \mathrm{RS}~=~7~\mathrm{cm} et \mathrm{RT}~=~4~\mathrm{cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Construire le triangle équilatéral \mathrm{FGH} tel que \mathrm{FG =} 5,5~\mathrm{cm}.
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Reproduire la figure ci-dessous en vraie grandeur en utilisant le codage.

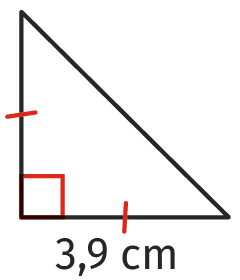


Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Placer un point \mathrm{L} sur la demi-droite \mathrm{[D}x) pour former un triangle \text{DEL} isocèle.
Chercher deux solutions différentes.
Chercher deux solutions différentes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
Dans chaque cas, construire à la règle non graduée et au compas des points \mathrm{E}, \mathrm{F} et \mathrm{G} tels que :
- \mathrm{ABE} est un triangle équilatéral ;
- \mathrm{CDF} est un triangle isocèle en \mathrm{F} ;
- \mathrm{BCG} est un triangle isocèle en \mathrm{C}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
On a tracé un segment \mathrm{[AB]} de longueur 5~\mathrm{cm}.


1. Peut-on construire un triangle \mathrm{ABC} tel que \mathrm{AC~=~BC}~=~2~\mathrm{cm} ? Justifier.
2. On souhaite construire un triangle \mathrm{ABC} tel que \mathrm{AC}~=~2~\mathrm{cm}. Quelle doit être la longueur minimale du segment \mathrm{[BC]} ? Justifier.
3. On souhaite construire un triangle \mathrm{ABC} tel que \mathrm{AC}~=~2~\mathrm{cm}. Existe-t-il une longueur maximale pour le côté \mathrm{[BC]} ? Justifier.


1. Peut-on construire un triangle \mathrm{ABC} tel que \mathrm{AC~=~BC}~=~2~\mathrm{cm} ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Relier trois des cinq points de la grille pour former les figures demandées.
1. Un triangle isocèle.
2. Un triangle rectangle.
2. Un triangle rectangle.
3. Un triangle isocèle-rectangle.
4. Un triangle isocèle-rectangle.
4. Un triangle isocèle-rectangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Énigme
Le maillage est formé de triangles équilatéraux.
Comment assembler ces trois triangles pour former un unique triangle équilatéral ?
Comment assembler ces trois triangles pour former un unique triangle équilatéral ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

