Thème 3 : Espace et géométrie
Fiche 43
Construire le cercle circonscrit à un triangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens l'essentiel
Propriété
Les trois médiatrices d'un triangle non plat sont sécantes en un unique point.
- Remarque :
On dit que les médiatrices du triangle sont concourantes.
Définition
À partir du point d'intersection des trois médiatrices du triangle, on peut construire le cercle centré en ce point et passant par les trois sommets du triangle. Ce cercle est appelé le cercle circonscrit au triangle.

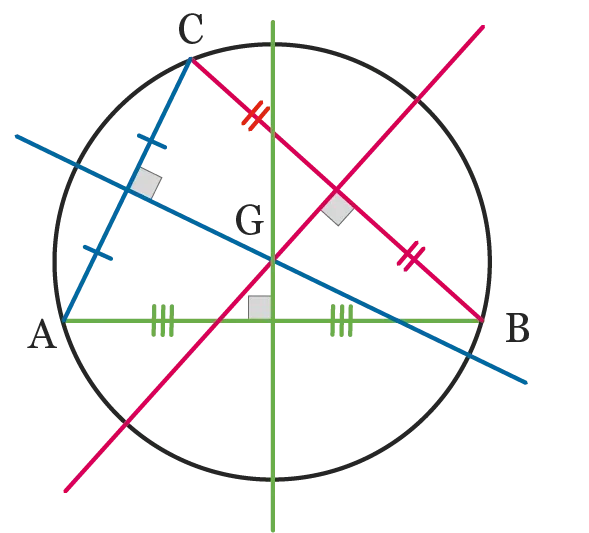
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
De la même manière que par deux points non
confondus passe une unique droite, l'existence
du cercle circonscrit indique que pour trois
points non alignés, il existe un unique cercle
passant par ces points.
▸ Plus d'informations en .
▸ Plus d'informations en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. \frac{223~121}{1~000}=
2. 1-\frac{1}{4}=
3. 1~\mathrm{dm}^2= \mathrm{cm}^2
2. 1-\frac{1}{4}=
3. 1~\mathrm{dm}^2=
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Copie d'élève
Copie d'élève
Line n'a pas réussi à construire le cercle circonscrit au triangle \mathrm{ABC}.

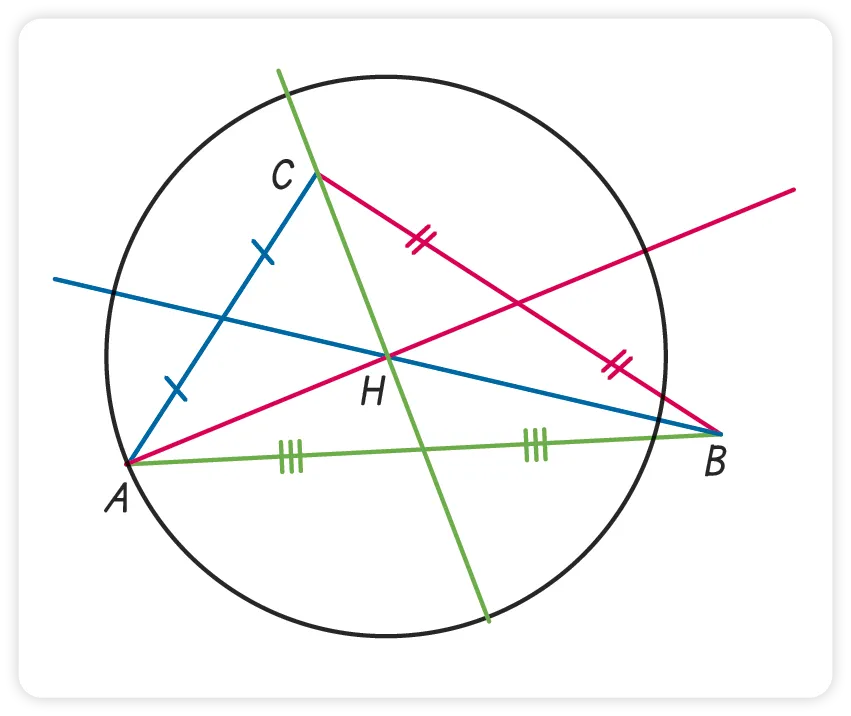
1. Quelle est son erreur ?
2. Corriger sa construction.


1. Quelle est son erreur ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Dans le triangle \mathrm{ABC} ci-dessous, on a construit les médiatrices des segments [\mathrm{AB}] et [\mathrm{AC}] et placé leur point d'intersection \mathrm{G}.

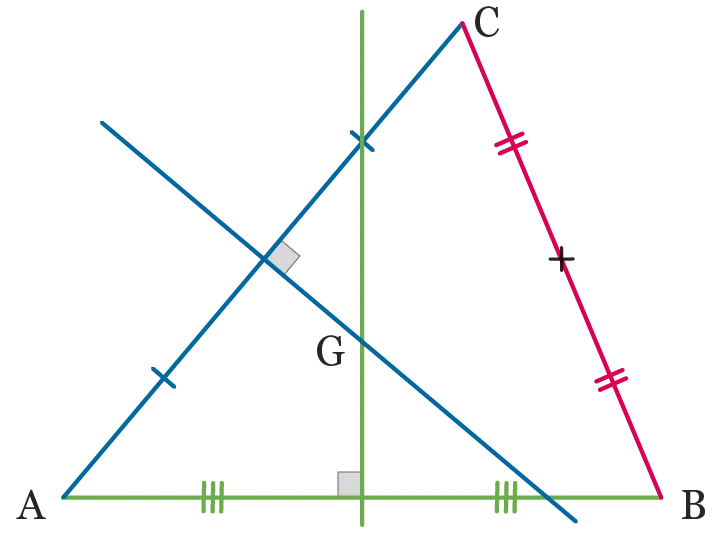


Compléter la démonstration de la concourence des trois médiatrices avec les égalités suivantes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
En utilisant uniquement le compas et la règle non graduée, construire le centre du cercle qui passe par les points \mathrm{A}, \mathrm{B} et \mathrm{C}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Le quadrillage ci-dessous est composé de triangles équilatéraux.
1. Quelle est la nature du triangle \mathrm{ABC} ?
2. Placer le centre de son cercle circonscrit.
1. Quelle est la nature du triangle \mathrm{ABC} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
1. En utilisant uniquement le quadrillage, placer le centre du cercle circonscrit au triangle \mathrm{ABC}.
2. Que remarque-t-on ?
2. Que remarque-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
On donne la figure ci-dessous.
Le point \mathrm{D} est-il sur le cercle passant par \mathrm{A}, \mathrm{B} et \mathrm{C} ?
Le point \mathrm{D} est-il sur le cercle passant par \mathrm{A}, \mathrm{B} et \mathrm{C} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Construire le triangle \mathrm{JUL} tel que (d_1) soit la médiatrice du segment [\mathrm{JU}] et (d_2) soit la médiatrice du segment [\mathrm{JL}].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Construire des points \mathrm{F} et \mathrm{L} tels que les droites (d_1) et (d_2) soient des médiatrices du triangle \mathrm{FLO}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Énigme
Reproduire les anneaux olympiques.

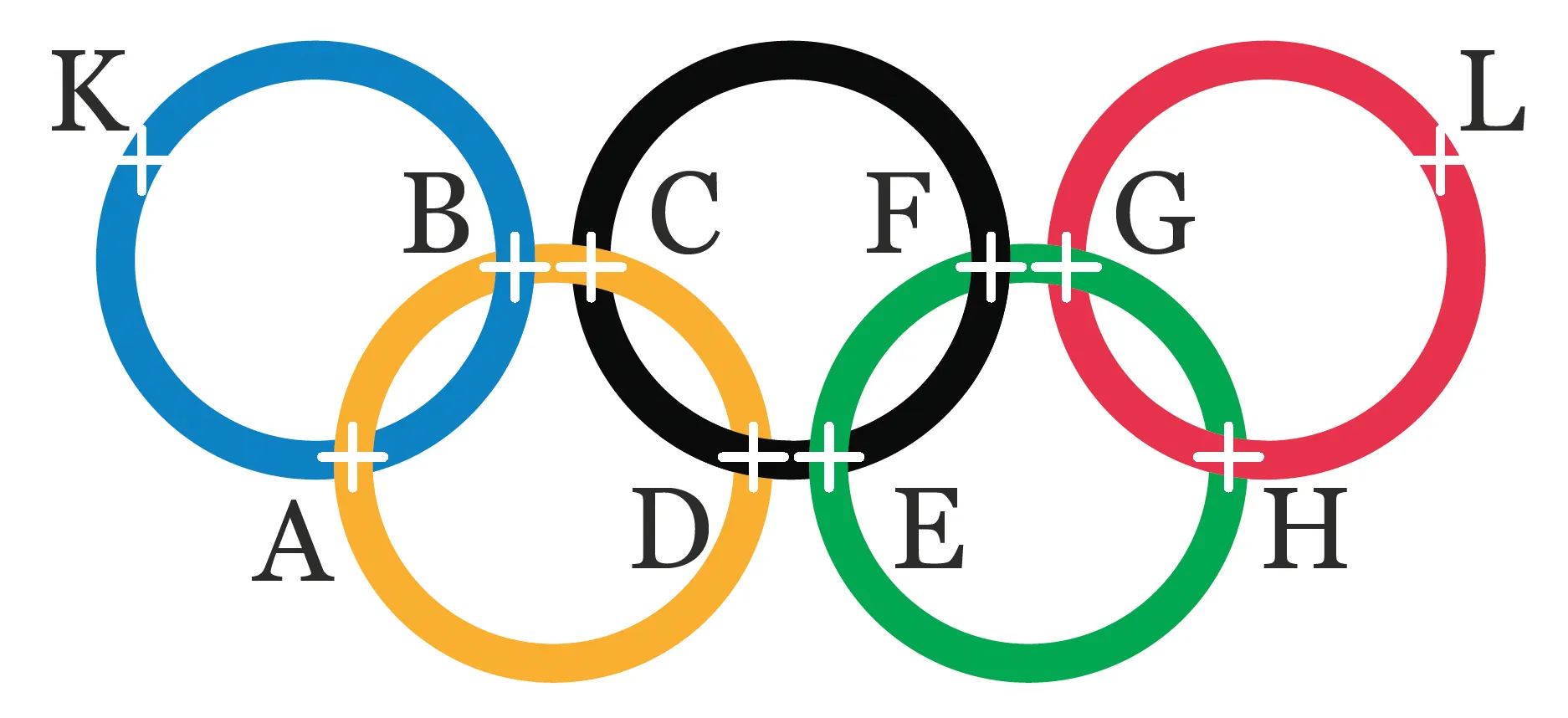

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

