Complément sur la dérivation

La fonction inverse définie sur \mathbb{R}^* par f(x)=\frac{1}{x} est dérivable sur tout intervalle de \mathbb{R}^* et sa fonction dérivée est définie, pour tout x \neq 0, par f^{\prime}(x)=\frac{-1}{x^2}.

Pour déterminer la fonction dérivée de la fonction g définie sur ] 0 ;+\infty[ par g(x)=\frac{4 x^2-7}{x}, on écrit, pour x>0, g(x)=\frac{4 x^2}{x}-7 \times \frac{1}{x}=4 x-7 \times \frac{1}{x}. Ainsi, pour tout x>0, g^{\prime}(x)=4-7 \times \frac{-1}{x^2}=4+\frac{7}{x^2}.

Dérivée d'un produit de fonctions
Soit u et v deux fonctions définies et dérivables sur un intervalle \mathrm{I}. Alors u \times v est dérivable sur \mathrm{I} et :

(u \times v)^{\prime}=u^{\prime} \times v+u \times v^{\prime}.

59

Déterminer les expressions des fonctions dérivées des fonctions suivantes définies pour x > 0.

1. f(x)=2 x^2-9 x+\frac{1}{x}

2. g(x)=x^3-10+\frac{3}{x}

3. h(x)=\frac{8 x^2+5 x-1}{x}

4. k(x)=\frac{-5 x^3+3 x^2+4}{x}

60

Déterminer les expressions des fonctions dérivées des fonctions f, g, h et k suivantes définies pour tout réel x différent de 0.

1. f(x)=\frac{x^2}{2}+\frac{2}{x}

2. g(x)=\frac{4 x^3-0,8 x^2-x+9}{x}

3. h(x)=\frac{1}{2 x}

4. k(x)=\frac{-1}{3 x}

61

En utilisant sa fonction dérivée, démontrer que la fonction inverse est décroissante sur ]-\infty ; 0[ et sur ] 0 ;+\infty[.

62

Construire le tableau de variations de la fonction f définie sur ]-2\:; 0[ par f(x)=x^2-\frac{2}{x}.

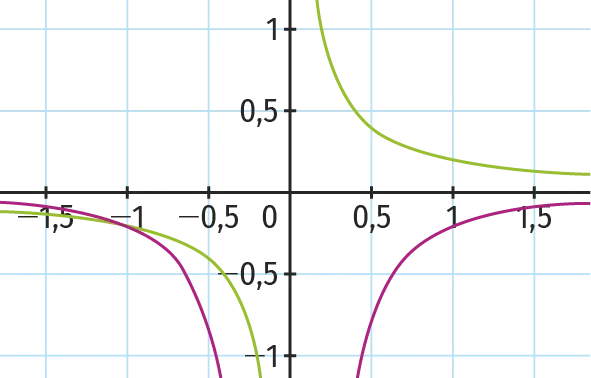
63

Sur le graphique ci-dessous, identifier les courbes représentatives de f : x \mapsto \frac{1}{5 x} et de sa fonction dérivée. Justifier.

64

La consommation en litre pour 100 km d'un véhicule est donnée, en fonction de sa vitesse x, en km/h, pour 20 \leqslant x \leqslant 100 par :

f(x)=\frac{0,5 x^2-36 x+800}{x}.

1. Exprimer f^{\prime}(x) en fonction de x \in[20 ; 100].

2. En déduire le signe de f^{\prime}(x) sur son ensemble de définition, puis les variations de f sur [20 ; 100].

3. Pour quelle vitesse du véhicule la consommation est-elle minimale ? Calculer cette consommation.

65

La vitesse d'une onde sonore en eau profonde est modélisée, en fonction de sa longueur d'onde x comprise entre 0,5 m et 50 m, par :

v(x)=1\;000 \sqrt{x+\frac{1}{x}}.

Afin de déterminer pour quelle longueur d'onde cette vitesse est minimale, on cherche le minimum sur l'intervalle [0,5 ; 50] de la fonction f=v^2, définie par f(x)=1\;000\;000 \times\left(x+\frac{1}{x}\right).



1. Exprimer f^{\prime}(x) en fonction de x.

2. Dresser le tableau de signes de f^{\prime}, puis le tableau de variations de f sur [0,5 ; 50].

3. En déduire la vitesse minimale d'une onde sonore dans l'eau.

66

Une agricultrice produit du lait. Elle estime que le coût de production en euro est donné, en fonction du volume produit en mètre cube, par :

C(x)=3 x^3-2,5 x^2+300 x+200.

On définit le coût moyen pour tout x > 0 par :

\mathrm{C}_{\mathrm{M}}(x)=\frac{\mathrm{C}(x)}{x}.

1. Donner l'expression de \mathrm{C}_{\mathrm{M}}(x) en fonction de x , puis celle de sa dérivée.

2. À l'aide d'une table de valeurs de \mathrm{C}_M^{\prime}(x), créée à l'aide d'un tableur par exemple, construire le tableau de signes de \mathrm{C}_M^{\prime}(x), le tableau de variations de \mathrm{C_M} et déterminer le volume de lait, arrondi au mètre cube, pour lequel le coût moyen est minimal.

3. Déterminer le coût moyen minimal.

67

Un producteur de safran estime que le coût de production de x kg de safran est donné, en euro, par C(x)=x^3-18 x^2+124 x+200.

Le coût moyen par kg de safran, exprimé en euro, sur une production de x kg est défini pour tout x>0 par \mathrm{C}_{\mathrm{M}}(x)=\frac{\mathrm{C}(x)}{x}.

1. Donner l'expression du coût moyen en fonction de x.

2. Montrer que, pour tout x > 0 :

\mathrm{C}_{\mathrm{M}}^{\prime}(x)=\frac{2(x-10)\left(x^2+x+10\right)}{x^2}.

Aide

On pourra commencer par montrer que, pour tout x>0, \mathrm{C}_{\mathrm{M}}^{\prime}(x)=\frac{2 x^3-18 x^2-200}{x^2}.

3. En déduire le tableau de signes de \mathrm{C}_{\mathrm{M}}^{\prime}(x), puis le coût moyen minimal. Pour quelle masse produite est-il atteint ?

68

Soit f la fonction définie, pour tout réel x, par f(x)=\left(x^2+4 x-5\right)(7 x+2).

1. Développer f(x) et en déduire f^{\prime}(x) pour tout réel x.

2. Retrouver ce résultat en utilisant la propriété de dérivation d'un produit de fonctions.

69

Soit g la fonction définie, pour tout réel x, par g(x)=\left(-2 x^3-3 x+1\right)(7 x+2).

1. Développer g(x). Peut‐on en déduire g^{\prime}(x) ?

2. Déterminer, pour tout réel x, une expression de g^{\prime}(x) en utilisant la propriété de dérivation d'un produit de fonctions.