Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonom étriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 7
Cours 1
Mesurer un angle en radian
8 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ACercle trigonométrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Dans un repère orthonormé (\text{O ; I , J}), le cercle trigonométrique \mathcal{C} est le cercle de centre \text{O} et de rayon 1 orienté dans le sens inverse des aiguilles d'une montre, appelé sens direct ou encore sens trigonométrique.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le sens des aiguilles d'une montre est appelé sens indirect.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BEnroulement de la droite numérique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On place la droite numérique perpendiculaire à \text { (OI) } telle que le 0 de la droite numérique coïncide avec le point \text{I} et on l'oriente dans le sens de \text{O} vers \text{J.} On enroule la demi-droite des réels positifs sur le cercle \mathcal{C} dans le sens trigonométrique et la demi-droite des réels négatifs sur le cercle \mathcal{C} dans le sens indirect.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
À chaque nombre réel x de la droite numérique, on associe un unique point \text{M} du cercle trigonométrique que l'on appelle point image.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Deux nombres réels x et x' de la droite numérique ont le même point image sur \mathcal{C} si et seulement si x=x^{\prime}+k \times 2 \pi avec k \in \mathbb{Z}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Cette propriété est une équivalence, elle est donc vraie dans les deux sens.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Principe : l'idée de la démonstration repose sur le fait que le périmètre du cercle trigonométrique a pour longueur 2\pi. Pour tout point \text{M} du cercle, on peut alors calculer la longueur de l'arc \overset{\Large{_{\frown}}}{\text{IM}} ou bien « parcourir » plusieurs fois le cercle jusqu'à revenir au point \text{M.} La longueur « parcourue » sera donc augmentée de 2\pi à chaque tour. En parcourant le cercle dans le sens indirect, on obtient les valeurs négatives.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On dit que x et x' sont égaux à 2\pi près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
En remarquant que \pi=3 \pi-1 \times 2 \pi=-5 \pi+3 \times 2 \pi, on en déduit que \pi, 3 \pi et -5 \pi ont le même point image sur le cercle trigonométrique : le point de coordonnées (-1 \: ; 0).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
À l'aide du cercle trigonométrique ci-contre, répondre aux questions suivantes en sachant que les points \text{F, O, C} appartiennent au cercle de centre \text{I} et de rayon \text{1.}
1. Quels sont les points images des réels \dfrac{\pi}{3},-2 \pi et \dfrac{3 \pi}{2}\:?
2. a. Que peut-on dire des points images des réels \dfrac{\pi}{4} et \dfrac{9 \pi}{4} ?
b. Donner deux autres nombres réels associés au même point image.
1. Quels sont les points images des réels \dfrac{\pi}{3},-2 \pi et \dfrac{3 \pi}{2}\:?
2. a. Que peut-on dire des points images des réels \dfrac{\pi}{4} et \dfrac{9 \pi}{4} ?
b. Donner deux autres nombres réels associés au même point image.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Pour trouver un point image :
2. Pour déterminer plusieurs réels associés au même point sur le cercle trigonométrique, il suffit d'ajouter ou de soustraire 2\pi au réel donné.
- on utilise le fait que la longueur du cercle trigonométrique est 2 \pi
- par proportionnalité, le demi-cercle mesure \pi et le quart de cercle mesure \dfrac{\pi}{2}
2. Pour déterminer plusieurs réels associés au même point sur le cercle trigonométrique, il suffit d'ajouter ou de soustraire 2\pi au réel donné.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. Le point image de \dfrac{\pi}{3} est \text{C.}
Le point image de -2\pi est \text{I.}
Le point image de \dfrac{3 \pi}{2} est \text{J'.}
2. a. \dfrac{9 \pi}{4}=\dfrac{\pi}{4}+2 \pi donc ils sont associés au même point image sur le cercle trigonométrique : le point \text{B.}
b. \dfrac{9 \pi}{4}+2 \pi=\dfrac{17 \pi}{4} et \dfrac{17 \pi}{4}+2 \pi=\dfrac{25 \pi}{4} sont également associés au point \text{B}.
Le point image de -2\pi est \text{I.}
Le point image de \dfrac{3 \pi}{2} est \text{J'.}
2. a. \dfrac{9 \pi}{4}=\dfrac{\pi}{4}+2 \pi donc ils sont associés au même point image sur le cercle trigonométrique : le point \text{B.}
b. \dfrac{9 \pi}{4}+2 \pi=\dfrac{17 \pi}{4} et \dfrac{17 \pi}{4}+2 \pi=\dfrac{25 \pi}{4} sont également associés au point \text{B}.
Pour s'entraîner
Exercices et p. 193
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CAngle en radian
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Le radian est la mesure d'un angle au centre qui intercepte sur \mathcal{C} un arc de longueur \text{1.}
Par conséquent 360^{\circ}=2 \pi rad, 180^{\circ}=\pi rad et 1 rad \approx 57\text{,}3^{\circ}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les angles en radian et en degré sont proportionnels.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le radian est noté rad.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
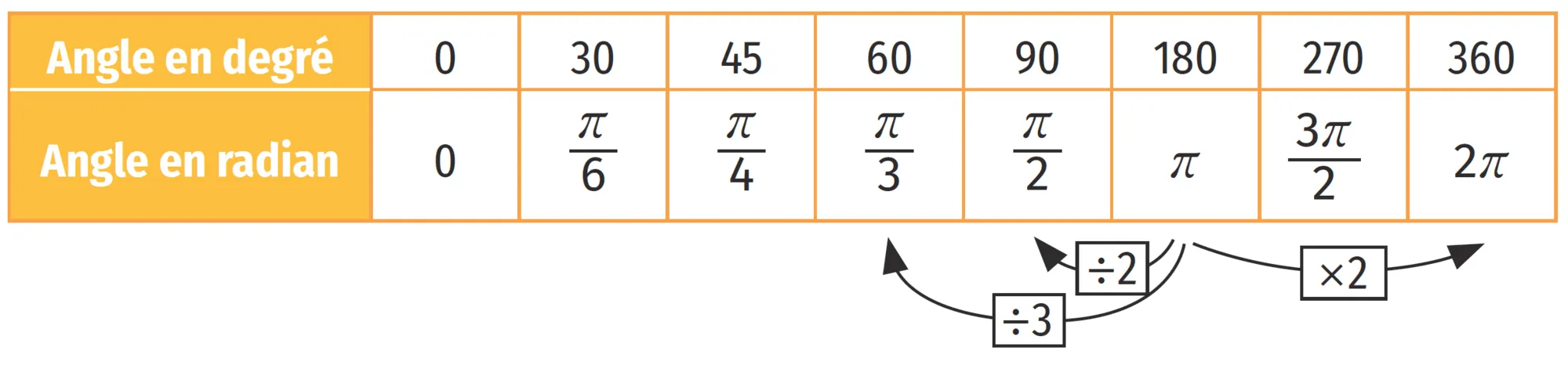
Énoncé
Compléter le tableau suivant.
| Angle en degré | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
| Angle en radian | \pi |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On utilise la proportionnalité d'un angle en radian et d'un angle en degré (180° = \pi rad).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah