17

Pour chacun des réels suivants, donner le signe de leur cosinus et de leur sinus.
\dfrac{\pi}{3} \:; \dfrac{-\pi}{3} \:; \dfrac{-2 \pi}{3}\: ; \dfrac{3 \pi}{3} \:; \dfrac{27 \pi}{3}.

18

Pour chacun des nombres suivants, déterminer un autre réel ayant le même point image lors de l'enroulement de la droite numérique.

\dfrac{\pi}{7}\: ; \dfrac{-\pi}{5}\: ; \dfrac{\pi}{6}\: ; \dfrac{2 \pi}{11} \:; \dfrac{-7 \pi}{4}.

20

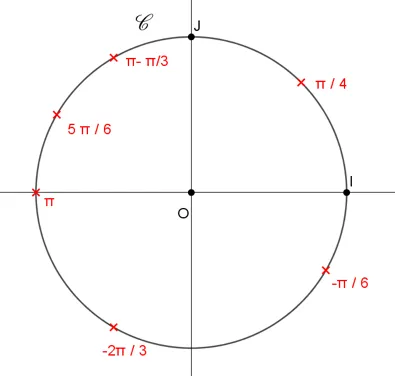
Tracer le cercle trigonométrique dans un repère orthonormé et y placer les réels suivants :
\pi \:; \dfrac{\pi}{4} \:; \dfrac{-\pi}{6} \:; \dfrac{-2 \pi}{3} \:; \dfrac{5 \pi}{6} \:; \pi-\dfrac{\pi}{3}.

21

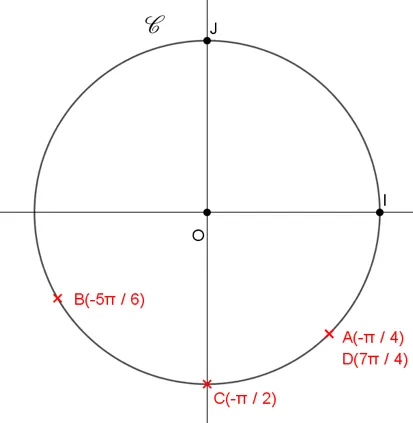
Tracer le cercle trigonométrique dans un repère orthonormé et placer les points \text{A, B, C} et \text{D} respectivement repérés par les réels \dfrac{-\pi}{4},-\dfrac{5 \pi}{6}, \dfrac{3 \pi}{2} et \dfrac{7 \pi}{4}.

22

On considère le réel \alpha=\dfrac{\pi}{6}. Donner tous les réels repérant le même point du cercle trigonométrique que \alpha.

23

Parmi les valeurs suivantes, quelles sont celles qui repèrent le même point sur le cercle trigonométrique ?

\dfrac{13 \pi}{6}\: ; \dfrac{-13 \pi}{6}\: ; \dfrac{11 \pi}{6}\: ; \dfrac{-11 \pi}{6} \:; \dfrac{25 \pi}{6} et \dfrac{-\pi}{6}.

24

Convertir les mesures suivantes en degré. Donner les valeurs exactes.

1. \dfrac{\pi}{16} rad

2. \dfrac{\pi}{72} rad

3. \dfrac{\pi}{7} rad

25

Convertir les mesures suivantes en radian. Donner les valeurs exactes.

1. 75^{\circ}

2. 120^{\circ}

3. 405^{\circ}

29

x est un nombre réel dont on donne le cosinus. Dans chaque cas, donner toutes les valeurs possibles du sinus associé. On donnera les valeurs exactes puis les valeurs approchées à 0{,}1 près si nécessaire.

1. \cos (x)=0{,}36

2. \cos (x)=0{,}7

3. \cos (x)=-0{,}8

4. \cos (x)=0

30

x est un nombre réel dont on donne le sinus. Dans chaque cas, donner toutes les valeurs possibles du cosinus associé. On donnera les valeurs exactes puis les valeurs approchées à 0{,}1 près si nécessaire.

1. \sin (x)=-0{,}9

2. \sin (x)=0{,}25

3. \sin (x)=\dfrac{4}{5}

4. \sin (x)=1

31

Vérifier, sans calculatrice, que \cos ^{2}(\alpha)+\sin ^{2}(\alpha)=1 lorsque :
\alpha=\dfrac{\pi}{3} \:; \alpha=\dfrac{-\pi}{4} \:; \alpha=\dfrac{5 \pi}{6} \:; \alpha=\dfrac{-\pi}{2}.

32

Sans utiliser la calculatrice, calculer \cos \left(\dfrac{\pi}{3}\right) \times \sin \left(\dfrac{\pi}{6}\right)+\sin (\pi).

33

Déterminer une valeur du réel x dans chacun des cas suivants.
1. \cos (x)=\dfrac{\sqrt{3}}{2} et \sin (x)=\dfrac{1}{2}.

2. \cos (x)=1 et \sin (x)=0.

3. \cos (x)=\dfrac{-\sqrt{2}}{2} et \sin (x)=\dfrac{\sqrt{2}}{2}.

34

x est un réel tel que \sin (3 x)=\dfrac{\sqrt{3}}{2}

1. Donner toutes les valeurs possibles pour 3x .

2. En déduire alors toutes les valeurs possibles pour x .

3. En déduire les solutions de l'équation \sin (3 x) sur l'intervalle ]-\pi\:; \pi ].