Les tours de Hanoï

Selon la légende, dans le temple de Bénarès sont plantées trois aiguilles de diamant. Le Dieu Brahmā a enfilé 64 disques d'or du plus grand au plus petit sur l'une des tiges. Les prêtres doivent déplacer ces disques d'une tige à l'autre en ne déplaçant qu'un disque à la fois sans jamais le poser sur un plus petit. La fin du monde arrivera lorsque les prêtres auront fini de déplacer ces 64 disques.

2. Pour n =3, déterminer le nombre minimal de coups en complétant les schémas ci-dessous, en indiquant le nombre de coups nécessaires pour passer d'une étape à l'autre.

3. Pour n \geqslant 1, on note d_n le nombre de déplacements nécessaires pour déplacer n disques d'une tige à une tige voisine. En complétant le schéma ci-dessous, en déduire que d_{n+1}=2d_n+1.

1. À l'aide de la calculatrice, donner une valeur approchée de d_{64}.

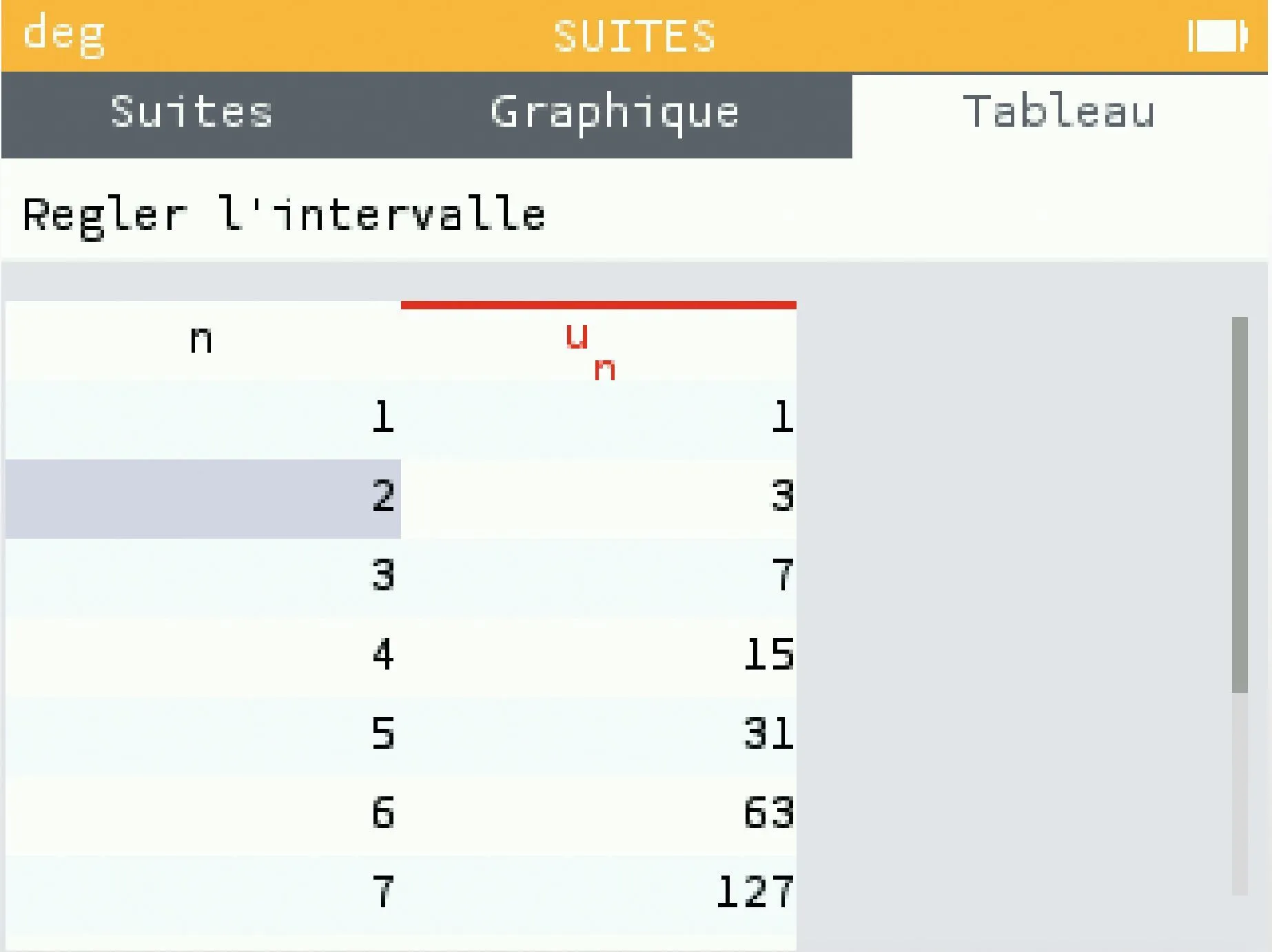
2. Sachant qu'il faut une seconde pour déplacer un disque, en déduire le nombre d'années nécessaires pour déplacer les 64 disques.

3. On définit pour tout entier n \geqslant 1, v_n = d_n +1.
a. Exprimer v_{n+1} en fonction de v_n.

b. En déduire la nature de la suite (v_n).

c. Exprimer v_n puis d_n en fonction de n.

d. En déduire la valeur exacte de d_{64} .

1. Compléter le programme ci-contre permettant de répondre à l'objectif.

def Deplacement(n):
  d = 1
  if n == 1:
    return(...)
  else:
    for i in range(...):
      d = ...
    return(...)

2. Sachant qu'il faut une seconde pour déplacer un disque, exécuter le programme pour déterminer le nombre d'années nécessaires pour déplacer les 64 disques (on pourra compléter le programme précédent ou créer une autre fonction pour calculer le temps nécessaire en secondes puis en années pour déplacer n disques).

3. On définit pour tout entier n\geqslant 1, v_n=d_n+1.
a. Exprimer v_{n+1} en fonction de v_n .

b. En déduire la nature de la suite (v_n).

c. Exprimer v_n puis d_n en fonction de n.

d. Retrouver la valeur de d_{64} à l'aide de cette formule et vérifier qu'elle correspond bien à la valeur donnée par le programme.